| Autor |
Nachricht |
Kathreena
Anmeldungsdatum: 27.03.2018
Beiträge: 96
|
 Kathreena Verfasst am: 15. Jun 2018 13:58 Titel: DGL, Durchflussmenge, Viskosität |
 |
|
Ein Trichter mit dem vollen Öffnungswinkel  ist bis zur Höhe H(t) mit Wasser gefüllt. Aus dem Trichter fließen aus einem waagrechten Rohr mit Innendurchmesser d und Länge L, Wasser in ein großes Gefäß.
a) Wie sieht der zeitliche Verlauf der Höhe H(t) des Wasserspiegels im Trichter aus?
b) Wie groß ist die Durchflussmenge des Wassers M(t)?
c) Nach welcher Zeit T ist das gesamte Wasser ausge
ossen, wenn H = 30 cm; d = 0,5 cm und L = 20 cm ist? Die Wassertemperatur beträgt T = 20° C und die Viskosität ) .
d.) Wie ändert sich die Zeit zum Befüllen eines Eimers mit einem Fassungsvermögen
von 4 Litern, wenn der Trichter durch kontinuierliches Nachfüllen mit V = 4 l vollgehalten wird.
Meine Idee:
a.)Also wenn ichs richtig verstanden habe ist  \cdot cos(60°))) der Durchmesser vom Trichter an der Öffnung. Und unten wo das Rohr angeschlossen ist, ist d.
 \cdot cos(60°)}{2})^2 \cdot \pi)
^2 \pi)
v_2 ist Geschwindigkeit im Rohr, v_1 Abflussgeschwindigkeit im Trichter.
DGL:
}{dt} = \frac{A_2}{A_1} \cdot \sqrt{2g} \sqrt{h} )
Dann Variablen trennen und Integrieren. Ich komme auf:
 = \frac{1}{4} ( \frac{A_2}{A_1} \cdot \sqrt{2g} \cdot t + C)^2)
Und um die Konstante zu finden, soll man glaub ich t=0 einsetzen. Aber dann kommt ja auch nix raus.
 = \frac{1}{4}(0+C)^2 = \frac{C^2}{4})
b.)
Ich nehme an der Volumenstrom ist gemeint.
oder
weiter komm ich nicht. |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5863
|
| Myon Verfasst am: 16. Jun 2018 09:56 Titel: |
|
|
Du hast bei Deiner Rechnung die gegebene Viskosität des Wassers nicht berücksichtigt. Bei Viskosität, Druckunterschied, Volumenstrom... sollte man an das Gesetz von Hagen-Poisseuille denken. Laut diesem ist der Volumenstrom 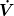 proportional zum Druckunterschied an den Enden des waagrechten Rohres mit der Länge L, und damit zur Höhe H des Wasserspiegels:
)
Zwischen V (dem Wasservolumen im Trichter) und H wiederum findet man einen geometrischen Zusammenhang, es ist
)
(r=Trichterradius auf der Höhe H). Damit ergibt sich aus dem Gesetz von Hagen-Poiseuille eine Differentialgleichung für V(t) oder H(t). |
|
|
Kathreena
Anmeldungsdatum: 27.03.2018
Beiträge: 96
|
| Kathreena Verfasst am: 16. Jun 2018 11:27 Titel: |
|
|
Ja weil ich dachte, das ist erst bei c.) zu berücksichtigen.
aber klar, wenn ich in a.) schon das berücksichtige, dann muss ich für c.) nurnoch die Werte einsetzen.
Muss mir nochmal anschaun wie du da einen geometrischen Zusammenhang rausliest. |
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5865
Wohnort: jwd
|
| Mathefix Verfasst am: 23. Jun 2018 18:56 Titel: |
|
|
zu a)
 = h^{2} \cdot \tan^{2} (\frac{\Phi}{2} ) \cdot \pi )
und damit
 \cdot \frac{\dd h}{\dd t} = \frac{d^{2} }{4} \cdot \sqrt{2\cdot g\cdot h} ) |
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5865
Wohnort: jwd
|
| Mathefix Verfasst am: 24. Jun 2018 12:12 Titel: |
|
|
Hinweis
Der Ansatz von Torricelli
\cdot \frac{\dd h}{\dd t} = A_2 \cdot \sqrt{2\cdot g\cdot h} )
gilt nur unter der Bedingung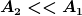 
Ansonsten gilt der Ansatz von Bernoulli über die Energieerhaltung. |
|
|
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5863
|
| Myon Verfasst am: 24. Jun 2018 12:26 Titel: |
|
|
|
Hallo Mathefix, wie ich schon oben geschrieben habe: Man muss hier die Viskosität berücksichtigen. Wieso wäre diese und die Länge L des Rohrs sonst gegeben? Und wie willst Du sonst den Aufgabenteil c) lösen? |
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5865
Wohnort: jwd
|
| Mathefix Verfasst am: 24. Jun 2018 13:21 Titel: |
|
|
| Myon hat Folgendes geschrieben: | | Hallo Mathefix, wie ich schon oben geschrieben habe: Man muss hier die Viskosität berücksichtigen. Wieso wäre diese und die Länge L des Rohrs sonst gegeben? Und wie willst Du sonst den Aufgabenteil c) lösen? |
Hallo Myon,
mein Hinweis bezog sich allein auf die Berücksichtigung der Behälter- und Ausflussfläche. Wenn man die Viskosität und Bernoulli berücksichtigt wird es richtig kompliziert.
Wenn also der vereinfachte Ansatz von Torricelli zulässig ist, kann die Viskosität nach Deinem Vorschlag (Hagen -P.) berücksichtigt werden, wobei noch die Frage offen ist, ob sie auch im Trichter zu berücksichtigen oder wg. geringer Sinkgeschwindigkeit vernachlässigbar ist.
Schönen Sonntach
Jörg |
|
|
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5863
|
| Myon Verfasst am: 24. Jun 2018 16:27 Titel: |
|
|
@Mathefix: der Volumenstrom ergibt sich aus dem Gesetz von Hagen-Poiseuille, ohne Bernoulli bzw. Torricelli.
Mit
^4}{8\eta L})
folgt aus dem Gesetz von Hagen-Poiseuille:
^\frac{1}{3})
oder
^\frac{1}{3}dt)
was man integrieren kann, womit man V(t) und daraus H(t) erhält. Die Viskosität im Trichter kann man vernachlässigen, da der Radius vergleichsweise gross (und  !) und die „Länge“ klein ist. Sonst würde es in der Tat kompliziert. |
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5865
Wohnort: jwd
|
| Mathefix Verfasst am: 24. Jun 2018 18:40 Titel: |
|
|
| Myon hat Folgendes geschrieben: | @Mathefix: der Volumenstrom ergibt sich aus dem Gesetz von Hagen-Poiseuille, ohne Bernoulli bzw. Torricelli.
Mit
folgt aus dem Gesetz von Hagen-Poiseuille:
oder
was man integrieren kann, womit man V(t) und daraus H(t) erhält. Die Viskosität im Trichter kann man vernachlässigen, da der Radius vergleichsweise gross (und !) und die „Länge“ klein ist. Sonst würde es in der Tat kompliziert. |
Wir reden wohl aneinander vorbei oder ich habe die Aufgabe nicht verstanden.
Meine Ausführungen beziehen sich auf a) und b). Da ist m.E. die Viskosität lt.Aufgabentext nicht zu berücksichtigen.
Mit Deiner Anwendung von H-P bin ich nicht ganz einverstanden.
Du hasst bei  nur den geodätischen Druck am Rohranfang berücksichtigt.
Es wirkt aber zusätzlich der dynamische Druck durch die Strömungsgeschwindigkeit.
Nach Bernoulli
)
mit
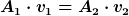
^{2} )
Ansonsten bin ich mit Deiner Rechnung einig. |
|
|
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5863
|
| Myon Verfasst am: 24. Jun 2018 23:29 Titel: |
|
|
|
Der dynamische Druck ist nicht relevant. Hagen-Poiseuille gibt den Druckunterschied an zwischen Anfang und Ende des waagrechten, dünnen Rohrs mit der Länge L. Die Strömungsgeschwindigkeit ist an beiden Punkten gleich. |
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5865
Wohnort: jwd
|
| Mathefix Verfasst am: 25. Jun 2018 09:28 Titel: |
|
|
| Myon hat Folgendes geschrieben: | | Der dynamische Druck ist nicht relevant. Hagen-Poiseuille gibt den Druckunterschied an zwischen Anfang und Ende des waagrechten, dünnen Rohrs mit der Länge L. Die Strömungsgeschwindigkeit ist an beiden Punkten gleich. |
Ich stelle ja nicht H-P infrage.
Deine Aussage stimmt nur dann, wenn Du die Sinkgeschwindigkeit (bei mir 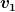) des Wasserspiegels im Trichter vernachlässigst. |
|
|
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5863
|
| Myon Verfasst am: 25. Jun 2018 11:03 Titel: |
|
|
| Mathefix hat Folgendes geschrieben: | | Deine Aussage stimmt nur dann, wenn Du die Sinkgeschwindigkeit (bei mir 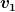des Wasserspiegels im Trichter vernachlässigst. |
Warum? |
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5865
Wohnort: jwd
|
| Mathefix Verfasst am: 25. Jun 2018 11:18 Titel: |
|
|
| Myon hat Folgendes geschrieben: | | Mathefix hat Folgendes geschrieben: | | Deine Aussage stimmt nur dann, wenn Du die Sinkgeschwindigkeit (bei mir 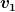des Wasserspiegels im Trichter vernachlässigst. |
Warum? |
Bezugsebene waagerechtes Rohr.
Ermittle nach Bernoulli den Gesamtdruck p_2 am Anfang des Rohres, dann siehst Du, dass die Sinkgeschwindigkeit v_1 des Wasserspiegels eingeht.
Sorry, hatte beim Ausklammern etwas übersehen. Die Formel muss lauten
 = \varrho \cdot g\cdot h\cdot ((\frac{A_2}{A_1(h)})^{2} -1) )
Annahme Torricelli: A_2 << A_1
 = -\varrho \cdot g\cdot h) |
|
|
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5863
|
| Myon Verfasst am: 25. Jun 2018 13:45 Titel: |
|
|
|
Ja, dass der Wasserspiegel langsam sinkt, wird hier vernachlässigt. Man könnte dies auch nicht einfach mit der Bernoulli-Gleichung berücksichtigen, da diese nur für ideale, viskosefreie Flüssigkeiten gilt. |
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5865
Wohnort: jwd
|
| Mathefix Verfasst am: 25. Jun 2018 14:36 Titel: |
|
|
| Myon hat Folgendes geschrieben: | | Ja, dass der Wasserspiegel langsam sinkt, wird hier vernachlässigt. Man könnte dies auch nicht einfach mit der Bernoulli-Gleichung berücksichtigen, da diese nur für ideale, viskosefreie Flüssigkeiten gilt. |
Ich bin der Meinung, dass Vereinfachungen in der Aufgabenstellung angegeben werden müssen, wie z.Bsp.: Viskosefreiheit im Trichter, Sinkgeschwindigkeit Wasserspiegel = 0, Strömungsgleichung nach Torricelli und nicht stillschweigend unterstellt werden dürfen.
Es ärgert mich, wenn das nicht so ist, da der Schüler/Student sich sonst einen Wolf rechnet und nicht in der vorgegebenen Zeit zu der Lösung kommt.
Man stelle sich die Rechnerei vor, wenn auch die Viskosität im Trichter berücksichtigt werden soll. Dann muss H-P bei nichtkonstantem Querschnitt hergeleitet werden  |
|
|
|
Registrieren
Login
FAQ
Suchen
