| Autor |
Nachricht |
jvc96
Anmeldungsdatum: 24.10.2016
Beiträge: 113
|
 jvc96 Verfasst am: 24. Nov 2017 23:31 Titel: Rückstoß bei Atomen jvc96 Verfasst am: 24. Nov 2017 23:31 Titel: Rückstoß bei Atomen |
 |
|
Hallo zusammen,
ich habe hergeleitet, dass bei der Berücksichtigung des Rückstoßes eines Atoms folgendes gilt:
)
Hierbei ist Delta E die Energiediferenz zwischen den Atomniveaus.
Jetzt soll ich die emittierte Wellenlänge von n=3 auf n=1 mit und ohne Rückstoß vergleichen.
Ohne gilt ja:
)
Aber ich komme nicht drauf, wie ich da jetzt den Rückstoß einbauen könnte.
Wäre schön, wenn da jemand helfen könnte  |
|
 |
jvc96
Anmeldungsdatum: 24.10.2016
Beiträge: 113
|
 jvc96 Verfasst am: 26. Nov 2017 01:36 Titel: jvc96 Verfasst am: 26. Nov 2017 01:36 Titel: |
 |
|
niemand der da helfen kann?  |
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 26. Nov 2017 14:00 Titel: Re: Rückstoß bei Atomen Huggy Verfasst am: 26. Nov 2017 14:00 Titel: Re: Rückstoß bei Atomen |
 |
|
| jvc96 hat Folgendes geschrieben: | Hallo zusammen,
ich habe hergeleitet, dass bei der Berücksichtigung des Rückstoßes eines Atoms folgendes gilt:
) |
Müsste sich wegen

hier nicht
)
ergeben? Davon mal abgesehen ist mir deine Fragen unverständlich. Mit  hast du wegen hast du wegen 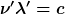 doch auch doch auch  . . |
|
 |
jvc96
Anmeldungsdatum: 24.10.2016
Beiträge: 113
|
 jvc96 Verfasst am: 26. Nov 2017 14:28 Titel: jvc96 Verfasst am: 26. Nov 2017 14:28 Titel: |
 |
|
also der Ausdruck müsste stimmen, weil das Ergebnis was rauskommen soll in der Aufgabe steht und meinem Ergebnis entspricht.
Ist das mit der Wellenlänge wirklich so einfach?
Ich setze also einfach nue in meine formel für nue' ein und berechne das dann? |
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 26. Nov 2017 14:51 Titel: Huggy Verfasst am: 26. Nov 2017 14:51 Titel: |
 |
|
| jvc96 hat Folgendes geschrieben: | | also der Ausdruck müsste stimmen, weil das Ergebnis was rauskommen soll in der Aufgabe steht und meinem Ergebnis entspricht. |
Ja, stimmt. Mir war beim Quadrieren eine 2 verloren gegangen.
| Zitat: | Ist das mit der Wellenlänge wirklich so einfach?
Ich setze also einfach nue in meine formel für nue' ein und berechne das dann? |
Die Beziehung zwischen Wellenlänge, Frequenz und Geschwindigkeit ist doch völlig allgemeingültig. |
|
 |
Conan
Gast
|
 Conan Verfasst am: 09. Dez 2023 10:06 Titel: Conan Verfasst am: 09. Dez 2023 10:06 Titel: |
 |
|
Der Thread ist schon recht alt.
Dürfte ich trotzdem fragen wo es diesen Rückstoß der Atome den gibt? |
|
 |
Conan
Gast
|
 Conan Verfasst am: 09. Dez 2023 10:20 Titel: Conan Verfasst am: 09. Dez 2023 10:20 Titel: |
 |
|
Der Thread ist schon recht alt.
Dürfte ich trotzdem fragen wo es diesen Rückstoß der Atome den gibt? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18068
|
 TomS Verfasst am: 09. Dez 2023 12:58 Titel: TomS Verfasst am: 09. Dez 2023 12:58 Titel: |
 |
|
Schau mal hier als Ausgangspunkt: Mößbauer-Effekt
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Conan
Gast
|
 Conan Verfasst am: 09. Dez 2023 15:35 Titel: Conan Verfasst am: 09. Dez 2023 15:35 Titel: |
 |
|
Vielen Dank!
Dieser Textausschnitt irritiert mich:
Die Temperatur von Festkörpern, Flüssigkeiten und Gasen ist korreliert mit der Geschwindigkeit der Teilchen (Atome, Moleküle) in denselben. Je höher die Temperatur, desto schneller bewegen sich die Teilchen im Mittel. Allerdings ist die Geschwindigkeit aller Teilchen nicht gleich, sondern statistisch verteilt, ebenso wie die Bewegungsrichtungen der Teilchen.
Mößbauer erwartete, dass mit steigender Temperatur die Wahrscheinlichkeit für eine Emission und anschließende Absorption eines Gamma-Quants ansteigen sollte, da sich statistisch gesehen mehr Atome mit der richtigen Geschwindigkeit aufeinander zubewegen. Umgekehrt sollte sich bei sehr niedrigen Temperaturen die Wahrscheinlichkeit für diesen Vorgang nahezu auf Null verringern, da die Atome im Mittel so langsam sind, dass die erforderliche Geschwindigkeitsdifferenz kaum einmal erreicht wird.
Soll ich das so verstehen, dass z.b. in einem Kristalgitter eines Metalls auch Atome vorhanden sind, die eben bei Raumtemperatur nicht nur um ihren Gitterplatz herum schwingen (höhere Temperatur dann höhere Amplitude der Schwingung) sondern die sich deutlich schneller und weiter bewegen als ihre "Artgenossen".
Ich dachte das getht gar nicht. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18068
|
 TomS Verfasst am: 09. Dez 2023 21:56 Titel: TomS Verfasst am: 09. Dez 2023 21:56 Titel: |
 |
|
Nein, du hast schon recht, die Atome schwingen nur um ihren Gitterplatz.
Die im Festkörper vorhandenen Schwingungen (Phononen) gehorchen den Regeln der Quantenmechanik. Dabei geht es nicht um die Schwingung eines einzelnen Atoms sondern um kollektive Freiheitsgrade. Stell dir vereinfacht untereinander verbundene Kugeln vor, die gemeinsam schwingen. Bei höheren Temperaturen werden zunehmend mehr sowie höherenergetische Schwingungen angeregt.
Im Falle der Streuung oder Absorption eines Gamma-Quants an bzw. durch einen Atomkern nimmt somit nicht der einzelne Atomkern sondern der gesamte Festkörper den Rückstoß auf.
EDIT: In der ursprünglichen Fragestellung ging es um die Absorption eines Photons durch ein Elektron der Atomhülle, beim Mößbauer-Effekt um die rückstoßfreie Kernresonanzabsorption von Gammastrahlung durch Atomkerne.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
|

















