| Autor |
Nachricht |
Wassergeist
Gast
|
 Wassergeist Verfasst am: 08. Nov 2017 13:52 Titel: Herleitung Orthogonalität Wassergeist Verfasst am: 08. Nov 2017 13:52 Titel: Herleitung Orthogonalität |
 |
|
Meine Frage:
Zeigen Sie, dass bei einer gleichförmigen Kreisbewegung der Vektor des Radius und der Vektor der Bahngeschwindigkeit einen rechten Winkel umschließen. Nehmen Sie als Grundlage an, dass sich der MP des Kreises in einem zweidimensionalen Koordinatensystem befindet.
Meine Ideen:
Wenn Vektor(r) und Vektor(v) einen rechten Winkel einschließen, sind sie ja orthogonal zueinander, d.h. das Skalarprodukt beider Vektoren ist 0.
Vektor(r)=Vektor(x)+Vektor(y), also Vektor(r)=(x|y) (=> Spaltenschreibweise untereinander)
Wie kann man jetzt Vektor (v) ausrechnen, damit Vektor(r)*Vektor(v)=0 gilt??? |
|
 |
Wassergeist
Gast
|
 Wassergeist Verfasst am: 08. Nov 2017 14:16 Titel: Wassergeist Verfasst am: 08. Nov 2017 14:16 Titel: |
 |
|
Habe ne Idee!
Wenn man sich denkt, dass der Vektor r exakt auf der x-Achse des hinzugefügten Koordinatensystems liegt, dann hat er ja die x-Komponente x und die y-Komponente 0.
Der Vektor der Geschwindigkeit kann ja jetzt auf die y-Achse verschoben werden (muss er zwar nicht, ist aber für mich anschaulicher), und hat dann die x-Komponente 0 und die y-Komponente y, sodass sich ergibt:
Vektor(r)*Vektor(v)=(x|0)*(0|y)=x*0+y*0=0+0=0 ==> Skalarprodukt 0, Winkel rechtwinklig
Habe ich was nicht bedacht? Bzw. gilt das jetzt für jeden Punkt des Kreises? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 08. Nov 2017 17:12 Titel: index_razor Verfasst am: 08. Nov 2017 17:12 Titel: |
 |
|
Ein Kreis um den Ursprung ist die Menge aller Punkte, deren Ortsvektor  konstante Norm konstante Norm

hat. Nun mußt du rechnnen
 |
|
 |
Wassergeist
Gast
|
 Wassergeist Verfasst am: 08. Nov 2017 18:01 Titel: Wassergeist Verfasst am: 08. Nov 2017 18:01 Titel: |
 |
|
Verstehe ich nicht ganz.
Der Ortsvektor geht ja immer vom KUS aus und sein Betrag ist konstant, er selbst nicht, weil er seine Richtung verändert während der Kreisbewegung.
Und was muss ich jetzt rechnen? Was ist die Ableitung vom Radius nach der Zeit, wie macht man das genau? Hatte das noch nicht genau in Mathe  |
|
 |
Wassergeist
Gast
|
 Wassergeist Verfasst am: 08. Nov 2017 18:17 Titel: Wassergeist Verfasst am: 08. Nov 2017 18:17 Titel: |
 |
|
|
Bzw. der Betrag vom Vektor r ist ja (Wurzel aus) x²+y² ... wie genau leitet man das ab? ... x² + y² wäre ja abgleitet 2x+2y, aber was passiert durch die Wurzel |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 08. Nov 2017 18:25 Titel: index_razor Verfasst am: 08. Nov 2017 18:25 Titel: |
 |
|
Nimm an die Bahnkurve des Teilchens ist ) . Daß die Bewegug auf einem Kreis mit Ursprung O verläuft, bedeutet doch genau, daß der Vektor . Daß die Bewegug auf einem Kreis mit Ursprung O verläuft, bedeutet doch genau, daß der Vektor
\stackrel{\rm{ def}}{=}\overrightarrow{OP(t)})
konstante, also zeitunabhängige, Norm hat. Das heißt, daß
\|^2 = \vec{r}(t)\cdot\vec{r}(t))
zeitunabhängig ist. Wenn du rechte Seite nach t ableitest was kommt dann also raus? Welche Ableitungsregeln für das Skalarprodukt kennst du, die du hier evtl. benutzen könntest? |
|
 |
Wassergeist
Gast
|
 Wassergeist Verfasst am: 08. Nov 2017 18:32 Titel: Wassergeist Verfasst am: 08. Nov 2017 18:32 Titel: |
 |
|
Ich kann keine Skalarprodukte ableiten, dass hatten wir nie ..
Gibt es auch eine andere Methode zur Herleitung?  |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 08. Nov 2017 18:44 Titel: index_razor Verfasst am: 08. Nov 2017 18:44 Titel: |
 |
|
Wie habt ihr denn die Begriffe "Betrag" eines Vektors und "Orthogonalität" eingeführt?
Wenn du weißt was ein Skalarprodukt und was eine Ableitung ist, ist es auch nicht schwer zu lernen, wie man Skalarprodukte ableitet. |
|
 |
Wassergeist
Gast
|
 Wassergeist Verfasst am: 08. Nov 2017 19:07 Titel: Wassergeist Verfasst am: 08. Nov 2017 19:07 Titel: |
 |
|
Ein Skalarprodukt ist die Summe von den Produkten der einzelnen Komponenten. Also man multipliziert die beiden x-Komponenten, usw. zusammen und addiert das.
Der Betrag eines Vektors ist dessen Länge, die kann man berechnen grob gesagt über den Pythagoras.
Der Vektor r(t) hat ja zwei Komponenten, ne x und ne y. ... wenn ich das Skalarprodukt bilde, habe ich ja dann x²+y², was abgeleitet 2(x+y) ist ...und jetzt? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 08. Nov 2017 19:10 Titel: index_razor Verfasst am: 08. Nov 2017 19:10 Titel: |
 |
|
| Wassergeist hat Folgendes geschrieben: |
Der Vektor r(t) hat ja zwei Komponenten, ne x und ne y. ... wenn ich das Skalarprodukt bilde, habe ich ja dann x²+y², was abgeleitet 2(x+y) ist ...und jetzt? |
Nein, das stimmt nicht. Wie leitest du denn da ab? Wenn r von der Zeit abhängt, dann auch seine Komponenten x und y. Du mußt |r|^2 = x^2 + y^2 nach t ableiten. |
|
 |
Wassergeist
Gast
|
 Wassergeist Verfasst am: 08. Nov 2017 19:15 Titel: Wassergeist Verfasst am: 08. Nov 2017 19:15 Titel: |
 |
|
hä? 
Aber wenn ich x²+y² ableite, kommt doch meins raus, oder 
Was isn die richtige Lösung?  |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 08. Nov 2017 19:20 Titel: index_razor Verfasst am: 08. Nov 2017 19:20 Titel: |
 |
|
| Wassergeist hat Folgendes geschrieben: | hä? :haue:
Aber wenn ich x²+y² ableite, kommt doch meins raus, oder :(
|
Nein, aber wenn du mir nicht verrätst, wie du darauf kommst, kann ich dir nicht erklären, was du falsch machst. Ich vermute, du hast keine besonders klare Vorstellung von dem Konzept "Ableitung".
Für die Ableitung von x^2(t) + y^2(t) benötigst du übrigens die Kettenregel. Hast du schon mal davon gehört? |
|
 |
Wassergeist
Gast
|
 Wassergeist Verfasst am: 08. Nov 2017 19:23 Titel: Wassergeist Verfasst am: 08. Nov 2017 19:23 Titel: |
 |
|
Naja, in Mathe nicht, aber in Physik ... LUL
Erst innen ableiten und das dran multiplizieren und dann außen.
also: x²(t)+y²(t)=2xt+2yt ??? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 08. Nov 2017 19:24 Titel: index_razor Verfasst am: 08. Nov 2017 19:24 Titel: |
 |
|
|
Rätst du jetzt nur? Was ist die "äußere Ableitung" und was ist die "innere Ableitung"? |
|
 |
Wassergeist
Gast
|
 Wassergeist Verfasst am: 08. Nov 2017 19:26 Titel: Wassergeist Verfasst am: 08. Nov 2017 19:26 Titel: |
 |
|
Deswegen sage ich ja die ganze Zeit, dass ich es nicht in Mathe hatte 
Ich nehme mal an, dass die innere funktion t und die äußere die jeweiligen Quadrate sind |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 08. Nov 2017 19:28 Titel: index_razor Verfasst am: 08. Nov 2017 19:28 Titel: |
 |
|
| Wassergeist hat Folgendes geschrieben: |
Ich nehme mal an, dass die innere funktion t und die äußere die jeweiligen Quadrate sind |
Die innere Funktion ist ) , die äußere , die äußere  . (Dasselbe gilt sinngemäß für die andere Komponente.) . (Dasselbe gilt sinngemäß für die andere Komponente.) |
|
 |
Wassergeist
Gast
|
 Wassergeist Verfasst am: 08. Nov 2017 19:31 Titel: Wassergeist Verfasst am: 08. Nov 2017 19:31 Titel: |
 |
|
Hast du nicht doch ne andere Variante ohne Kettenregel?  Ich hab echt überhaupt keine Ahnung davon Ich hab echt überhaupt keine Ahnung davon |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 08. Nov 2017 19:33 Titel: index_razor Verfasst am: 08. Nov 2017 19:33 Titel: |
 |
|
|
Bist du nicht gerade aus dem Grund hier, um "Ahnung" von etwas zu bekommen? Ich habe noch keine Vorstellung davon, welche Erklärung für dich verständlich wäre. |
|
 |
Wassergeist
Gast
|
 Wassergeist Verfasst am: 08. Nov 2017 19:35 Titel: Wassergeist Verfasst am: 08. Nov 2017 19:35 Titel: |
 |
|
Ja sicher, aber wenn ich die Grundlagen noch nicht hatte, kann ich es auch nicht verstehen 
Deswegen frage ich ja, ob es vielleicht was gibt, wo man den Vektor v aufstellen kann und dann zeigen kann, dass das Skalarprodukt aus v und r 0 ist |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 08. Nov 2017 19:38 Titel: index_razor Verfasst am: 08. Nov 2017 19:38 Titel: |
 |
|
| Wassergeist hat Folgendes geschrieben: | Ja sicher, aber wenn ich die Grundlagen noch nicht hatte, kann ich es auch nicht verstehen :(
|
Und was hindert dich nun an der Anwendung der Kettenregel? |
|
 |
Wassergeist
Gast
|
 Wassergeist Verfasst am: 08. Nov 2017 19:44 Titel: Wassergeist Verfasst am: 08. Nov 2017 19:44 Titel: |
 |
|
Das ich sie nicht wirklich verstanden habe 
Wenn ich jetzt nur x² * t betrachte, ist das doch nur eine Funktion mit Faktor  |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 08. Nov 2017 19:50 Titel: index_razor Verfasst am: 08. Nov 2017 19:50 Titel: |
 |
|
| Wassergeist hat Folgendes geschrieben: |
Wenn ich jetzt nur x² * t betrachte, ist das doch nur eine Funktion mit Faktor :haue: |
Was willst du immer noch mit x^2*t? Davon hat außer dir niemand gesprochen.
Wir reden von der Ableitung von ]^2 + [y(t)]^2) nach t. Nun hast du selbst gesagt, daß du hier jeweils die äußere Ableitung und die innere Ableitung bilden und anschließend beides multiplizieren mußt. Was ist jetzt das Problem: die äußere Ableitung? die innere Ableitung? ... nach t. Nun hast du selbst gesagt, daß du hier jeweils die äußere Ableitung und die innere Ableitung bilden und anschließend beides multiplizieren mußt. Was ist jetzt das Problem: die äußere Ableitung? die innere Ableitung? ... |
|
 |
Wassergeist
Gast
|
 Wassergeist Verfasst am: 08. Nov 2017 20:04 Titel: Wassergeist Verfasst am: 08. Nov 2017 20:04 Titel: |
 |
|
|
Wenn ich (x[t])² habe, dann leite ich erstmal außen ab und hab dann: 2(x[t]) ... wenn ich jetzt aber noch die inner dranpacke, dann bleibt das doch gleich, weil die ableitung von x ist 1, oder? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 08. Nov 2017 20:07 Titel: index_razor Verfasst am: 08. Nov 2017 20:07 Titel: |
 |
|
| Wassergeist hat Folgendes geschrieben: | | Wenn ich (x[t])² habe, dann leite ich erstmal außen ab und hab dann: 2(x[t]) ... wenn ich jetzt aber noch die inner dranpacke, dann bleibt das doch gleich, weil die ableitung von x ist 1, oder? |
x(t) ist die x-Komponente des Ortsvektors zur Zeit t. Deren Ableitung nach t ist nicht 1, sondern die x-Komponente der Geschwindigkeit zur Zeit t. |
|
 |
Wassergeist
Gast
|
 Wassergeist Verfasst am: 08. Nov 2017 20:12 Titel: Wassergeist Verfasst am: 08. Nov 2017 20:12 Titel: |
 |
|
|
also ist die gesamte Ableitung : 2[x(t)]*v(t)+2[y(t)]2+v(t) ??? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 08. Nov 2017 20:15 Titel: index_razor Verfasst am: 08. Nov 2017 20:15 Titel: |
 |
|
| Wassergeist hat Folgendes geschrieben: | | also ist die gesamte Ableitung : 2[x(t)]*v(t)+2[y(t)]2+v(t) ??? |
Ich vermute mal das letzte "+" ist ein Tippfehler. Nun mußt du nur noch vermeiden, für die x- und y-Komponente der Geschwindigkeit denselben Buchstaben v zu verwenden. Gebräuchlich sind Bezeichnungen wie 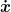 oder oder 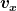 für die x-Komponente (und analog für die y-Komponente) der Geschwindigkeit. für die x-Komponente (und analog für die y-Komponente) der Geschwindigkeit.
Wie lautet dann alles zusammengenommen? |
|
 |
Wassergeist
Gast
|
 Wassergeist Verfasst am: 08. Nov 2017 20:18 Titel: Wassergeist Verfasst am: 08. Nov 2017 20:18 Titel: |
 |
|
|
2[x(t)]*vx(t) + 2[y(t)]*vy(t) |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 08. Nov 2017 20:22 Titel: index_razor Verfasst am: 08. Nov 2017 20:22 Titel: |
 |
|
Richtig. Nun nochmal zur Erinnerung: dies war die Zeitableitung von |r|^2, welches wiederum zeitunabhängig war, da die Bewegung auf einem Kreis erfolgt.
Was folgt nun daraus? |
|
 |
Wassergeist
Gast
|
 Wassergeist Verfasst am: 08. Nov 2017 20:24 Titel: Wassergeist Verfasst am: 08. Nov 2017 20:24 Titel: |
 |
|
Bevor wir weitermachen ... kannst du mir nochmal bitter erklären, warum die Ableitung von x(t) v(t) ist?  |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 08. Nov 2017 20:28 Titel: index_razor Verfasst am: 08. Nov 2017 20:28 Titel: |
 |
|
|
Die meisten würden das als die Definition der (momentanen) Geschwindigkeit ansehen. Was verstehst du denn unter Geschwindigkeit? |
|
 |
Wassergeist
Gast
|
 Wassergeist Verfasst am: 08. Nov 2017 20:34 Titel: Wassergeist Verfasst am: 08. Nov 2017 20:34 Titel: |
 |
|
|
Also ist das die Geschwindigkeit in dem Punkt P ... ok, weil die erste Ableitung des Weges nach der zeit die Geschwindigkeit ist, richtig? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 08. Nov 2017 20:37 Titel: index_razor Verfasst am: 08. Nov 2017 20:37 Titel: |
 |
|
| Wassergeist hat Folgendes geschrieben: | | Also ist das die Geschwindigkeit in dem Punkt P ... ok, weil die erste Ableitung des Weges nach der zeit die Geschwindigkeit ist, richtig? |
Ja, wir haben ja  = x(t)\vec{e}_x + y(t)\vec{e}_y.) Die Ableitung davon ist Die Ableitung davon ist
 = \dot x(t)\vec{e}_x + \dot y(t)\vec{e}_y= v_x(t)\vec{e}_x + v_y(t)\vec{e}_y) |
|
 |
Wassergeist
Gast
|
 Wassergeist Verfasst am: 08. Nov 2017 20:40 Titel: Wassergeist Verfasst am: 08. Nov 2017 20:40 Titel: |
 |
|
|
Ok, gut, das habe ich soweit verstanden, wie gehts jetzt weiter? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 08. Nov 2017 20:47 Titel: index_razor Verfasst am: 08. Nov 2017 20:47 Titel: |
 |
|
|
Hier steht der nächste Hinweis. |
|
 |
Wassergeist
Gast
|
 Wassergeist Verfasst am: 08. Nov 2017 20:52 Titel: Wassergeist Verfasst am: 08. Nov 2017 20:52 Titel: |
 |
|
Fällt mir gerade nichts ein ... kannst du mir einen tipp geben, ist schon ziemlich spät  |
|
 |
Wassergeist
Gast
|
 Wassergeist Verfasst am: 09. Nov 2017 15:53 Titel: Wassergeist Verfasst am: 09. Nov 2017 15:53 Titel: |
 |
|
Wie gehts weiter? Mir fällt es echt nicht ein  |
|
 |
Wassergeist
Gast
|
 Wassergeist Verfasst am: 09. Nov 2017 18:54 Titel: Wassergeist Verfasst am: 09. Nov 2017 18:54 Titel: |
 |
|
?  |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 09. Nov 2017 20:17 Titel: index_razor Verfasst am: 09. Nov 2017 20:17 Titel: |
 |
|
|
Wie geläufig ist dir denn der Begriff der Ableitung überhaupt? Was ergibt die Ableitung einer zeitlich konstanten Größe nach der Zeit? |
|
 |
|




















