| Autor |
Nachricht |
Silencium92
Anmeldungsdatum: 24.01.2017
Beiträge: 59
|
 Silencium92 Verfasst am: 14. Mai 2017 16:23 Titel: Quantenzahlen Silencium92 Verfasst am: 14. Mai 2017 16:23 Titel: Quantenzahlen |
 |
|
Guten Tag,
ist unserer Experimentalphysik Vorlesung zu Quantenmechanik haben wir "grob" die Schrödingerglg. für das Wasserstoffatom gelöst und dabei die ganzen Quantenzahlen eingeführt, wobei ich l,m noch nicht so wirklich verstanden habe.
Für verschiedene Hauptquantenzahlen n mit l=0 ist die Aufenhaltswahrscheinlichkeit im Kern maximal (siehe Lösungen der Radialschrödingerglg.) und für l ungleich 0 minimal.
Kann mir das bitte mal jemand erklären?
Ich weiß, dass das Effektive Potential für l=0 nur aus der Coulombpotential bestehen und bei l ungleich 0 kommt ein Potenial ~ 1/r^2 hinzu.
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 14. Mai 2017 17:11 Titel: Myon Verfasst am: 14. Mai 2017 17:11 Titel: |
 |
|
Für l=0 ist zwar die Radialfunktion 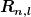 maximal. Die Wahrscheinlichkeit für einen Aufenthalt zwischen r und r+dr ist aber maximal. Die Wahrscheinlichkeit für einen Aufenthalt zwischen r und r+dr ist aber
dr=r^2|R_{n,l}|^2dr)
W(r) geht für 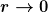 gegen 0, d.h. die Wahrscheinlichkeit für einen Aufenthalt im Kern ist immer gleich null. gegen 0, d.h. die Wahrscheinlichkeit für einen Aufenthalt im Kern ist immer gleich null.
|
|
 |
Silencium92
Anmeldungsdatum: 24.01.2017
Beiträge: 59
|
 Silencium92 Verfasst am: 14. Mai 2017 17:41 Titel: Silencium92 Verfasst am: 14. Mai 2017 17:41 Titel: |
 |
|
Okay, könntest du mir aber erklären warum die Radialfunktion für l=0 maximal ist und l ungleich minimal?
Hat es was mit dem Effektiven Potential zu tuen?
|
|
 |
gnt
Gast
|
 gnt Verfasst am: 14. Mai 2017 18:10 Titel: gnt Verfasst am: 14. Mai 2017 18:10 Titel: |
 |
|
Bei l>0 ist Drehimpuls vorhanden; das "effektive Potential" ist soz. die Fliehkraft. Von daher liegen die Maxima der Aufenthaltswahrscheinlichkeitsdichte weiter draussen.
Die Aufenthaltswahrscheinlichkeitsdichte würde ich nicht auf diese Weise betrachten. - Bei l=0 liegt das Maximum von R bei r=0, aber man kann nicht einfach mit 1/r² multiplizieren, um die Aufenthaltswahrscheinlichkeitsdichte bei einem Punkt r, theta, phi zu erhalten; bei einer einfachen Multiplikation erhält man die Summe der Dichte für eine Kugelschale.
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 14. Mai 2017 18:28 Titel: Myon Verfasst am: 14. Mai 2017 18:28 Titel: |
 |
|
Die Radialfunktionen ergeben sich als Lösungen der Radialgleichung - nach ziemlich viel Rechnen. Wieso sie genau so verlaufen, habe ich mir bis jetzt nicht überlegt und kann ich auch nicht sagen, sorry.
@gnt: Wegen der radialen Aufenthaltswahrscheinlichkeitsdichte - das habe ich doch genau so geschrieben. Natürlich ist Wahrscheinlichkeitsdichte bei ) gleich gleich |^2) . .
|
|
 |
gnt
Gast
|
 gnt Verfasst am: 14. Mai 2017 18:58 Titel: gnt Verfasst am: 14. Mai 2017 18:58 Titel: |
 |
|
|
@Myon: Das habe ich nicht korrekt formuliert. Was mich an Deinem Beitrag irritiert hat, war "...die Wahrscheinlichkeit für einen Aufenthalt im Kern ist immer gleich null.". Das kann man so nicht sagen, weil diese Aussage nur für eine abstrakte Funktion bei r=0 gültig ist. Diese Funktion ist in der Tat abhängig von r², sagt aber nichts über die Wellenfunktion oder |psi|² bei r=0 aus.
|
|
 |
gnt
Gast
|
 gnt Verfasst am: 14. Mai 2017 19:17 Titel: gnt Verfasst am: 14. Mai 2017 19:17 Titel: |
 |
|
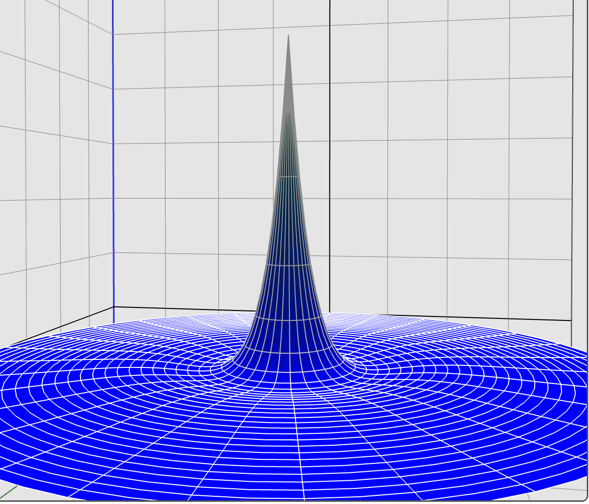
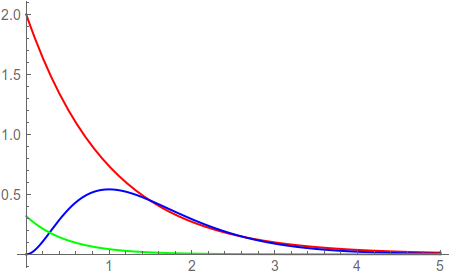
Hab' schnell ein Photo gemacht.
Rot=R
Blau=|R|²r²
Grün=|psi|²
|R|²r² zeigt nicht den Wert real existierender Punkte. Soweit sind wir uns ja einig. Deshalb darf man nicht sagen: "...die Wahrscheinlichkeit für einen Aufenthalt im Kern ist immer gleich null."
| Beschreibung: |
|
| Dateigröße: |
12.98 KB |
| Angeschaut: |
1704 mal |
|
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 14. Mai 2017 19:18 Titel: Myon Verfasst am: 14. Mai 2017 19:18 Titel: |
 |
|
|
@gnt: OK, Du hast recht... da muss man in der Tat aufpassen. Die obige Folgerung, dass wegen W(r) gegen 0 für r gegen 0 die Aufenthaltswahrscheinlichkeit beim Kern =0 ist, ist nicht richtig.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 15. Mai 2017 08:11 Titel: TomS Verfasst am: 15. Mai 2017 08:11 Titel: |
 |
|
Ich denke, das wesentliche Problem ist die sprachlich unpräzise Formulierung, nicht die Mathematik.
Zunächst ist die Wahrscheinlichkeitsdichte gegeben; die kann man für einen Punkt berechnen. Dann ist nach der Wahrscheinlichkeit gefragt; die kann man jedoch nur für einen Bereich betrachten. Um nun nicht Äpfel mit Birnen zu vergleichen, muss man z.B. die Wahrscheinlichkeit innerhalb verschiedener Kugelschalen (eine davon mit Innenradius Null für den Kern) mit identischem Volumen vergleichen.
Andernfalls vergleicht man mathematische Funktionen, ohne deren Bedeutung zu verstehen.
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
|
 |
gnt
Gast
|
 gnt Verfasst am: 15. Mai 2017 13:05 Titel: gnt Verfasst am: 15. Mai 2017 13:05 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | | PS: Was mich einfach schon etwas irritiert: dann ist es doch so, dass zumindest bei den Zuständen 1s, 2s, 3s die Aufenthaltswahrscheinlichkeit pro Volumeneinheit beim Kern am höchsten ist? |
Ja, je weiter man Richtung r=0 kommt, desto grösser ist die Aufenthaltswahrscheinlichkeitsdichte, also einmal von den Wellen abgesehen. Das liegt daran, dass dort die potentielle Energie niedriger als weiter weg ist, und weil der Energieeigenwert konstant ist, muss die Krümmung(=kin. Energie) stärker sein.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 16. Mai 2017 07:14 Titel: TomS Verfasst am: 16. Mai 2017 07:14 Titel: |
 |
|
Wie wär's, das mal zu berechnen? Also
 = 4\pi \int_R^{R+\dd r} \dd r \, r^2)
 = 4\pi \int_R^{R+\dd r} \dd r \, r^2 \, |\psi_{n00}(r)|^2)
für kleines, variables dr, so dass dV = const.
Was kommt da raus?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
|
 |
gnt
Gast
|
|
 |
|