Quantenzahlen

falcon_1 · Gast

Meine Frage:
Bei der Atomphysik verwirrt mich momentan die Vielzahl von Quantenzahlen und ähnlichen Bezeichnungen. Ich habe das Thema auch schon in verschiedenen Büchern und Webseiten nachgelesen, aber da die Bezeichnungen dort unterschiedlich verwendet wurden, hat mir das kaum geholfen.
Vielleicht kann mir ja hier jemand weiterhelfen!

Meine Ideen:
Also, für ein Elektron gibt es diese Quantenzahlen:

- Hauptquantenzahl n=0,1,2,... (Energieniveau)
- Drehimpulsquantenzahl l=0,1,...,n-1 (Form des Orbitals)
- Magnetische Quantenzahl m_l=-l,...,l (z-Komponente des Drehimpulses)
- Spinquantenzahl s=1/2
- Magnetische Spinquantenzahl m_s=-1/2,+1/2.

Soweit ist mir das noch klar. Dann kann man ja bei Mehrelektronensystemen "Gesamtdrehimpuls" bzw. "Gesamtspin" bilden:

Mit den Quantenzahlen J (Gesamtdrehimpuls), L (Gesamtbahndrehimpuls) und S (Gesamtspin).
Nun lese ich immer wieder, dass L und S durch die Summe der einzelnen Drehimpulse/Spins gebildet werden.

Da stellt sich mir die Frage: Welche Quantenzahlen werden hier summiert? "Der Spin" z.B. ist für mich die Quantenzahl s=1/2. Aber die wird hier doch nicht summiert, denn wie könnte dann der Gesamtspin S=0 zustande kommen?

Werden also die z-Komponenten summiert, also die m_l bzw. m_s, um auf Gesamtdrehimpuls bzw. Gesamtspin zu kommen? Gilt also z.B. die Formel

Gelesen habe ich das so aber noch nirgends!

Was mich weiter verwirrt: L scheint nicht nur die Gesamtdrehimpulsquantenzahl zu bezeichnen, sondern auch den Betrag des Drehimpulses mit

.

Dabei handelt es sich doch um ein völlig anderes Objekt, oder? Manchmal wird in der letzten Formel auch ein Vektorpfeil über dem L geschrieben, manchmal nicht.

Vielleicht könnte hier jemand etwas Licht ins Dunkel bringen?

Danke!!

Beste Grüße
Falcon

ScoreMagnet · Anmeldungsdatum: 25.05.2019 Beiträge: 8

Hallo.

Zunächst einmal: n = Energieniveau stimmt zwar, aber ist doch nicht ganz richtig. Denn die Energieniveaus können sich je nach ihren anderen Quantenzahlen noch weiter aufspalten.

Beim Gesamtspin addierst du schon die Spins, die können als Spin Up oder Spin Down auftauchen ,wenn du Fermionen mit s=1/2 hast, also + und - als Vorzeichen.

Das L in deiner Formel unten ist nicht die Gesamtdrehimpulsquantenzahl, sondern der Drehimpulsoperator und das auf der rechten Seite des Gleichheitszeichens ist sein Eigenwert, wenn du ihn auf eine Wellenfunktion anwendest.

TomS · Moderator Anmeldungsdatum: 20.03.2009 Beiträge: 18067

Zur Frage der Drehimpulsaddition:

Operatoren zu verschiedenen und daher kommutierenden Einzeldrehimpulsen oder Einzelspins werden ganz einfach addiert. Nehmen wir zwei Einzeldrehimpulse i=1,2 sowie jeweils die entsprechendem Eigenzustände

Die Operatoren für das selbe i erfüllen die üblichen Vertauschungsrelationen für a=x,y,z; b=x,y,z und c=x,y,z

Die Operatoren für verschiedene i,k vertauschen

Kompakt mittels Kronecker-Symbol

Eine gemeinsame Eigenbasis stammt aus dem Produkthilbertraum; rechts die übliche kompakte Schreibweise

Die Operatoren auf diesem Produkthilbertraum werden wie folgt gebildet:

Analog für die Drehimpulsquadrate.

Die Anwendung auf die Zustände erfolgt gemäß

Damit erkennt man, dass diese Basis für dem Produkthilbertraum wieder eine Eigenbasis ist. Die beiden Dehimpulse können in dieser Basis isoliert betrachtet werden, der jeweils andere Drehimpuls stört nicht. Das oben Gesagte gilt für beliebige unabhängige Drehimpulse, also insbs.
a) Bahndrehimpuls und Spin eines Teilchens
b) die Bahndrehimpulse zweier Teilchen
Beispiele für (b) wären die Drehimpulse zweier Elektronen der Atomhülle oder Drehimpulse eines Elektrons sowie des Kerns.

Wenn dir diese Voraussetzungen klar sind, dann können wir mit der Addition der Drehimpulse weitermachen. Diese Addition - die etwas verwickelter ist - wird z.B. dann benötigt, wenn man
a) den Gesamtdrehimpuls als Summe von Bahndrehimpuls und Spin eines Teilchens
b) den Gesamtbahndrehimpuls zweier Teilchen als Summe der einzelnen Bahndrehimpulse
betrachten möchte.

falcon_1 · Gast

Vielen vielen Dank erstmal für eure Antworten. Teilweise habe ich aber noch Fragen:

@ ScoreMagnet: Was sind denn "die Spins"? Die Spinquantenzahl s ist doch für Elektronen immer s=1/2, also ohne Minus!
Oder meinst du die z-Komponente, mit der Quantenzahl m_s?

Stimmt also diese Formel hier:

oder nicht?
Bzw. analog

?

@ TomS: Leider kann ich dir nicht folgen, weil mir die (mathematischen) Grundlagen fehlen. Ich bin auch nicht in der theoretischen Physik, sondern in der Experimentalphysik unterwegs. Sorry!
Ich hatte gehofft, dass es einen "einfachen" praktischen Weg gibt, den Gesamtspin aus den Quantenzahlen der einzelnen Elektronen zu bestimmen?

TomS · Moderator Anmeldungsdatum: 20.03.2009 Beiträge: 18067

Für zwei Drehimpulse ist die Formel zur Additon der z-Komponengen richtig.

Aber für den Gesamtdrehimpuls bzw. dessen Quadrat existiert im Allgemeinen keine vergleichbar einfache Formel zur Addition.

Und sorry, du wirst die Notation zumindest lesen und verstehen müssen ...

falcon_1 · Gast

Danke für die Rückmeldung!

TomS · Moderator Anmeldungsdatum: 20.03.2009 Beiträge: 18067

Moment, du verwechselst die Hundschen Regeln *) zur Besetzung von Schalen mit den allgemeinen Regeln zur Drehimpulsaddition. Die Hundschen Regeln gelten lediglich in Spezialfällen.

Das Problem ist folgendes - leider wieder in der vorliegen Notation.

Wir betrachten zwei Teilsysteme wie oben, die zu einem Gesamtsystem mit einem definierten Gesamtdrehimpuls gekoppelt werden sollen. Für den Gesamtdrehimpulsoperator gilt

Gesucht sind dessen Eigenzustände

mit

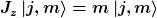
Nun kann man diese Eigenzustände nach der im letzten Beitrag konstruierten Eigenbasis des Gesamtsystems entwickeln.

Die Entwicklungskoeffizienten werden Clebsch–Gordan-Koeffizienten genannt.

Nun stellt man folgendes fest: um einen Eigenzustand |jm> zu erhalten, kann man - abhängig von der Orientierung d.h. abhängig von den beiden m-Werten - nicht einfach zwei beliebige Zustände rechts addieren; man muss rechts entsprechend der Clebsch–Gordan-Koeffizienten addieren, sonst ist das Ergebnis links kein Eigenzustand.

D.h. weder zerfällt der neue Eigenzustand |jm> immer in eine Summe genau zweier Eigenzustände rechts, noch ergibt eine Summe genau zweier Eigenzustände rechts immer einen Eigenzustand |jm>.

Einfach ist es eigentlich immer nur dann, wenn beiden Drehimpulse „parallel“ oder „antiparallel“ sind, d.h. wenn für i=1,2

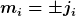
gilt, und insbs. dann, wenn sich beide m-Werte zu Null addieren, also

Das ist aber bei Spins in Orbitalen oft der Fall: Die beiden Spins in einem Orbital koppeln gerade zu Null (antiparallel), der Gesamtspin eines Orbitals verschwindet, und damit hast du für diesen zwei-Elektronen-Zustand speziell

Bzw. die beiden Spins in zwei verschiedenen Orbitalen der selben Schale koppeln gerade zu Eins (parallel).

Darüberhinaus spielt es bei mehr als zwei Teilsystemen eine Rolle, in welcher Reihenfolge du die Drehimpulse koppelst. Bei zwei Elektronen hast du vier zu koppelnde Drehimpulse, nämlich zwei Bahndrehimpulse und zwei Spins; es ist ein Unterschied, ob du die LS-Kopplung oder die JJ-Kopplung betrachtest. LS: erst beide Bahndrehimpulse zu L sowie beide Spins zu S, dann J = L+S; JJ: erst jeweils Spin- und Bahndrehimpuls je eines Elektrons zu je einem Gesamtdrehimpuls, dann beide Gesamtdrehimpulse der beiden Elektronen.

Hier ist der wesentliche Punkt, dass bei wechselwirkenden Elektronen gar nicht klar ist, welche Drehimpulse überhaupt „gute“ Quantenzahlen sind. Das einzige, was wir sicher wissen ist, dass man das gesamte Atom als in einem Gesamt-Eigenzustand des Drehimpulses über alle Elektronen befindlich ansetzen darf; die Bahndrehimpulse der einzelnen Elektronen müssen überhaupt keine guten Quantenzahlen sein.

Die Hundschen Regeln sind demnach gerade Spezialfälle der LS-Kopplung in (insbs. leichten) Atomen.

*) Achtung: in diesem Artikel werden die Werte der Drehimpulse mit Großbuchstaben bezeichnet.