| Autor |
Nachricht |
Zombiepriester
Anmeldungsdatum: 05.12.2016
Beiträge: 62
|
|
 |
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8578
|
 jh8979 Verfasst am: 12. Mai 2017 19:44 Titel: |
 |
|
|
Da das alles Dummy-Indizes sind, über die summiert wird, kannst Du die einfach umbenennen wie Du lustig bist.
|
|
|
Zombiepriester
Anmeldungsdatum: 05.12.2016
Beiträge: 62
|
| Zombiepriester Verfasst am: 12. Mai 2017 19:50 Titel: |
|
|
Wirklich? Wenn ich in der Mitte dieses  einfach in  umbenennen würde, würden die Summanden in ihrer Zusammensetzung bei Ausführung der Summenkonvention doch was Anderes ergeben.
 x^\lambda) ungleich  oder?
|
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8578
|
| jh8979 Verfasst am: 12. Mai 2017 20:11 Titel: |
|
|
| Zombiepriester hat Folgendes geschrieben: |
ungleich oder? |
Ja, aber der erste Ausdruck macht auch gar keinen Sinn mit diesen Indizes.
(Du musst natürlich alle Indizes konsistent umbenennen. So kannst Du natürlich keinen Namen wählen, den schon andere Summationsindizes im selben Term haben. Es sei denn Du benennst diese auch um.)
|
|
|
Zombiepriester
Anmeldungsdatum: 05.12.2016
Beiträge: 62
|
| Zombiepriester Verfasst am: 12. Mai 2017 20:16 Titel: |
|
|
|
Ja der Ausdruck macht keinen Sinn, das war nur ein Beispiel. Aber um das h mit dem Lambda und das h mit dem my unter einen Index zu bringen hilft es mir ja nix, die umzubenennen, weil sie ja trotzdem immer unterschiedliche Indezies haben werden, egal wie ich die nenne.
|
|
|
APWBDumbledore
Gast
|
| APWBDumbledore Verfasst am: 12. Mai 2017 20:19 Titel: |
|
|
|
Wie würdest Du es finden, einfach die Euler-Lagrange-Gleichung zu verwenden, anstatt die Variationen von Hand zu berechnen? So solltest Du die Geodätengleichung mit den korrekten Christoffelsymbolen recht schnell bekommen.
|
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8578
|
| jh8979 Verfasst am: 12. Mai 2017 20:20 Titel: |
|
|
| APWBDumbledore hat Folgendes geschrieben: | | Wie würdest Du es finden, einfach die Euler-Lagrange-Gleichung zu verwenden, anstatt die Variationen von Hand zu berechnen? So solltest Du die Geodätengleichung mit den korrekten Christoffelsymbolen recht schnell bekommen. |
Da man die Euler-Lagrange-Gleichung durch Variation erhält, kommt offensichtlich dasselbe raus.
|
|
|
APWBDumbledore
Gast
|
| APWBDumbledore Verfasst am: 12. Mai 2017 21:57 Titel: |
|
|
Ich wollte auch nichts Gegenteiliges behaupten. Die Rechnung fällt allerdings wesentlich kürzer aus:
 = g_{\mu \nu} (x) \dot x^\mu \dot x^\nu)
Und fertig (man muss nur beim Koeffizientenvergleich beachten, dass die Koeffizientenmatrix einer quadratischen Form bloß bis auf einen antisymmetrischen Anteil eindeutig ist, d.h. man muss symmetrisieren, um Eindeutigkeit zu erreichen).
Mir tat einfach der OP leid, dass er so eine lange Rechnung ohne Ergebnis hatte. Deswegen wollte ich einen kürzeren Weg vorschlagen, der es ermöglicht, die wesentlichen Schritte im Blick zu behalten.
|
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8578
|
| jh8979 Verfasst am: 12. Mai 2017 22:14 Titel: |
|
|
| APWBDumbledore hat Folgendes geschrieben: | Ich wollte auch nichts Gegenteiliges behaupten. Die Rechnung fällt allerdings wesentlich kürzer aus:
|
Sicher, weil man die Rechnung ja schon ausgeführt hat...
|
|
|
Zombiepriester
Anmeldungsdatum: 05.12.2016
Beiträge: 62
|
| Zombiepriester Verfasst am: 12. Mai 2017 23:27 Titel: |
|
|
|
Ich hab den Weg über die Larangegleichung auch schon angesehen, aber ich wollte halt den Weg "pur" direkt über die Variation gehen. Wie gesagt, ich dachte es wär interessant und vor allem auch eine gute Übung.
|
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8578
|
| jh8979 Verfasst am: 13. Mai 2017 04:25 Titel: |
|
|
| Zombiepriester hat Folgendes geschrieben: | | Ich hab den Weg über die Larangegleichung auch schon angesehen, aber ich wollte halt den Weg "pur" direkt über die Variation gehen. Wie gesagt, ich dachte es wär interessant und vor allem auch eine gute Übung. |
Ist es ja auch 
|
|
|
Zombiepriester
Anmeldungsdatum: 05.12.2016
Beiträge: 62
|
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8578
|
| jh8979 Verfasst am: 14. Mai 2017 11:52 Titel: |
|
|
| Zombiepriester hat Folgendes geschrieben: | Ok, ich hab jetzt diese Umsortierungstechnik angewandt, hat auch echt lange gedauert, sah zuerst gut aus, aber ich bin irgendwie ganz knapp dran vorbei  |
Dann hast Du Dich wohl verrechnet 
|
|
|
Zombiepriester
Anmeldungsdatum: 05.12.2016
Beiträge: 62
|
| Zombiepriester Verfasst am: 14. Mai 2017 19:17 Titel: |
|
|
|
Ach was Ich hatte gehofft, jemand könnte mir beim Errorspotting helfen, aber eigentlich kann ich sehr gut nachvollziehen, wenn man sich da als Fremder nicht reinbegeben will...
|
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8578
|
| jh8979 Verfasst am: 14. Mai 2017 20:00 Titel: |
|
|
| Zombiepriester hat Folgendes geschrieben: | | Ach was Ich hatte gehofft, jemand könnte mir beim Errorspotting helfen, aber eigentlich kann ich sehr gut nachvollziehen, wenn man sich da als Fremder nicht reinbegeben will... |
In der Tat
Selbst wenn das meine eigene Rechnung wäre, würde ich mir das nicht durchlesen Ich denke Du solltest nochmal von vorne anfangen und es auch per Hand machen (also nicht am Computer), das reduziert copy-paste-Fehler, die hier gerne auftreten.
|
|
|
Zombiepriester
Anmeldungsdatum: 05.12.2016
Beiträge: 62
|
| Zombiepriester Verfasst am: 15. Mai 2017 11:52 Titel: |
|
|
Ok, aber mir ist grad eine potentielle Fehlerquelle aufgefallen: Eine grundlegende Frage: wie indiziert man die Ableitung der Metrik? Ich hab ja eine Metrik, die ich auch mal ableiten muss. ich hab für jede Ableitung lambda als Index benutzt, weil die Metrik davon abhängt.
)
Aber dieser Index ist ja eher symbolischer Natur um eben hervorzuheben, dass g von der Position abhängt. Ist es also richtig in der Ableitung Lambda zu übernehmen, oder ist es sogar sinnvoller für jede Ableitung einen anderen Index zu nutzen?
|
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8578
|
| jh8979 Verfasst am: 15. Mai 2017 11:57 Titel: |
|
|
| Zombiepriester hat Folgendes geschrieben: | | Ist es also richtig in der Ableitung Lambda zu übernehmen, oder ist es sogar sinnvoller für jede Ableitung einen anderen Index zu nutzen? |
Solange Du es richtig machst, kannst Du das halten wie Du willst. Du wirst wahrscheinlich eh Indizes umbenennen müssen, um am Ende auf die gewünschte Form zu kommen.
|
|
|
APWBDumbledore
Gast
|
| APWBDumbledore Verfasst am: 15. Mai 2017 13:11 Titel: |
|
|
Nur um sicher zu gehen: War die Frage, was günstig ist, oder was richtig ist?
Die Ableitung des metrischen Tensors hat keine geometrische Bedeutung, sie ist kein Tensor. Allerdings sind die Ableitungen jeder Komponente des metrischen Tensors selbst Tensorfelder von kovariantem Rang 1, und so ist es richtig, wenn man im Bereich einer Karte
als Tensorfeld von kovariantem Rang 3 auffasst (der abhängig von der Karte definiert ist, d.h. er "transformiert sich nicht wie ein Tensor"). Insofern ist aber der Index alpha nicht symbolisch, im Gegensatz zum Index lambda in ) , der lediglich andeutet, dass x Koordinaten hat.
Entscheidend ist, dass du eine Variation berechnest, also
 = \frac{\partial g_{\mu \nu}}{\partial x^\alpha} \delta h^\alpha (x)
<br />
+ \dots) ,
das heißt der Index alpha (bei dir lambda) tritt paarweise in einer Einstein-Summe auf. Du benennst also entweder beide Indizes um oder gar keinen, das ist deiner Freiheit überlassen.
|
|
|
Zombiepriester
Anmeldungsdatum: 05.12.2016
Beiträge: 62
|
| Zombiepriester Verfasst am: 15. Mai 2017 19:33 Titel: |
|
|
Ok, was ich meinte: Ist es legitim den ganzen Term so zu schreiben?
 + irgendwas + \partial_\beta g_{\mu \nu}(x^\lambda) + irgendwas2 + \partial_\alpha g_{\mu \nu}(x^\lambda) ...)
Und bei der Variation muss man ja schon auf den Index achten, also:
 = \partial_{\beta} g_{\mu \nu}(x^{\lambda} + \epsilon h^{\lambda}) h^{\beta})
Ist das dann so auch legitim, obwohl der Index links ja Lambda ist?
|
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8578
|
| jh8979 Verfasst am: 15. Mai 2017 19:36 Titel: |
|
|
Ich würde das Argument einfach x nennen und den Index lambda weglassen. Der ist nicht nötig für die Rechnung, er mach das Rechnen nur unübersichtlicher. Da sind schon genug Indizes.
PS: Ich würde sogar das ganze Argument weglassen der Übersichtlichkeit halber. Es ist klar, welche der Objekte Funktionen von x sind.
|
|
|
Zombiepriester
Anmeldungsdatum: 05.12.2016
Beiträge: 62
|
| Zombiepriester Verfasst am: 19. Mai 2017 20:02 Titel: |
|
|
|
Ok, ich hab jetzt nochmal ganz neu angefangen und für alles was "neu dazukam" einen neuen Index eingeführt. Hört sich zuerst dumm an, allerdings war der Hintergedanke dann Indexe gleichzusetzen damit es aufgeht. Hat aber auch nicht funktioniert. Jetzt steh ich mit einem riesigen unvereinfachbaren komplizierten Term da. Ich denke ich hör auf das zu probieren, es geht anscheinend einfach nicht. Trotzdem danke für eure Hilfe.
|
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8578
|
| jh8979 Verfasst am: 19. Mai 2017 20:44 Titel: |
|
|
Jetzt wollte ich mich selber hinsetzen und es Dir aufschreiben, und da fiel mir das Problem, das auftaucht, auf. Sorry, hatte ich wohl schon verdrängt Vermutlich, weil ich an die Rechnung dachte, wenn das Integral über Vierergeschwindigkeit im Quadrat geht und nicht mit der Wurzel.
(Was zum selben Ergebnis führt... cum grano salis)
Man erhält die Geodaetengleichung nämlich nur, wenn man die Kurve mit einem affinen Parameter parametrisiert (wie z.B. der Eigenzeit). Das kann man von unterschiedlichen Punkten angehen.. im Endeffekt bedeutet es, dass du beim partiellen Integrieren, die Ableitung auf das 1/√ ignorieren kannst(und dann lösen sich in Deiner Rechnung sicherlich alle Probleme in Wohlgefallen auf).
Details dazu findest Du z.B. hier
https://physics.stackexchange.com/questions/94348/geodesics-equations-via-variational-principle
Hier wird das geschickt benutzt (und nicht wirklich explizit erwähnt)
http://people.uncw.edu/hermanr/GR/geodesic.pdf
Sorry, dass Du da jetzt ne Woche lang dran rumgerechnet hast wie irre... Aber naja, sollte ja eine Übung sein und bin sicher im Indizes rumschubsen bist Du jetzt sehr geübte
|
|
|
Zombiepriester
Anmeldungsdatum: 05.12.2016
Beiträge: 62
|
| Zombiepriester Verfasst am: 20. Mai 2017 19:50 Titel: |
|
|
Ja ok, diese Transformation von in meinem Fall s zurück zu 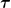 zurechnen und dadurch die Wurzeln loszuwerden ist natürlich schon praktisch. Also wenn ich das richtig verstehe, ist meine Rechnung an sich nicht falsch (bis auf einen Ableitungsfehler der mir grad aufgefallen ist, fällt aber nicht ins Gewicht), bloß führt die nicht auf die gängige Form der Geodätengleichung, weil ich den allgemeinen Kurvenparameter nicht zur Eigenzeit transformiere.
|
|
|
Zombiepriester
Anmeldungsdatum: 05.12.2016
Beiträge: 62
|
| Zombiepriester Verfasst am: 20. Mai 2017 21:30 Titel: |
|
|
|
Also gilt die Geodätengleichung in der Form nur mit Ableitungen nach der Eigenzeit. Allerdings hab ich in Skripts auch schon Die Geodätengleichung mit Ableitung nach s oder eben lambda gesehen. Ist das dann eine Ungenauigkeit ("künstlerische Freiheit")?
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18047
|
| TomS Verfasst am: 20. Mai 2017 23:23 Titel: |
|
|
| Zombiepriester hat Folgendes geschrieben: | | Also gilt die Geodätengleichung in der Form nur mit Ableitungen nach der Eigenzeit. Allerdings hab ich in Skripts auch schon Die Geodätengleichung mit Ableitung nach s oder eben lambda gesehen. Ist das dann eine Ungenauigkeit ("künstlerische Freiheit")? |
Du kannst die Kurvenlänge s durch eine streng monotone, jedoch ansonsten beliebige Funktion f(s) ersetzen; du musst nur die Kettenregel anwenden.
Im Falle lichtartiger Geodäten entspricht der Parameter nie der Eigenzeit bzw. Länge, da diese konstant Null sind.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8578
|
| jh8979 Verfasst am: 21. Mai 2017 00:04 Titel: |
|
|
| Zombiepriester hat Folgendes geschrieben: | | Also gilt die Geodätengleichung in der Form nur mit Ableitungen nach der Eigenzeit. Allerdings hab ich in Skripts auch schon Die Geodätengleichung mit Ableitung nach s oder eben lambda gesehen. Ist das dann eine Ungenauigkeit ("künstlerische Freiheit")? |
Na ja, die Eigenzit ist nicht die einzige Parametrisierung, die funktioniert. Aber die physikalisch voll meist sinnvollste.*
*alles natürlich nur für zeitartige Geodäten wie Tom schon anmerkte.
|
|
|
APWBDumbledore
Gast
|
| APWBDumbledore Verfasst am: 21. Mai 2017 02:20 Titel: |
|
|
| Zombiepriester hat Folgendes geschrieben: | | Also gilt die Geodätengleichung in der Form nur mit Ableitungen nach der Eigenzeit. Allerdings hab ich in Skripts auch schon Die Geodätengleichung mit Ableitung nach s oder eben lambda gesehen. Ist das dann eine Ungenauigkeit ("künstlerische Freiheit")? |
Nein, viel besser. Eine Kurve, die die Geodätengleichung erfüllt, ist automatisch nach einem affinen Parameter parametrisiert.
Im Gegensatz zur Lagrangefunktion  ist die Wirkung bzgl. der Lagrangefunktion  nicht vom Kurvenparameter unabhängig. Sie führt allerdings in jedem Fall zur Geodätengleichung (auch für lichtartige und zeitartige Geodäten, nebenbei). Und eine Version des Noethertheorems garantiert dir für jeden Extrempunkt des Wirkungsfunktionals die Konstanz von  entlang der Kurve (analog der Energieerhaltung in der klassischen Mechanik, bloß dass die Symmetrie hier nicht die Homogenität der Zeit, sondern die Homogenität des Kurvenparameters ist).
|
|
|
APWBDumbledore
Gast
|
| APWBDumbledore Verfasst am: 21. Mai 2017 23:48 Titel: |
|
|
PS: Also ob die Geodätengleichung nur Geodäten in Parametrisierung nach einem affinen Parameter beschreibt, hängt davon ab, wie Du eine Geodäte definierst...
- Extrempunkt des Längenfunktionals: ja, nur dann.
- Extrempunkt des Energiefunktionals: immer, denn das ist automatisch der Fall.
- Kurve, die  erfüllt: immer, denn das ist automatisch der Fall, denn
 , \dot \gamma (t) \rangle = \frac{\nabla}{\mathrm d t} \langle \dot \gamma (t) , \dot \gamma (t) \rangle = 2 \langle \frac{\nabla}{\mathrm d t} \dot \gamma (t) , \dot \gamma (t) \rangle = 0)
|
|
|
|
Registrieren
Login
FAQ
Suchen
