| Autor |
Nachricht |
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
 Amateurphysiker Verfasst am: 01. Apr 2017 16:45 Titel: Spezifische Wärme von Gasen (Legendre Transformation) Amateurphysiker Verfasst am: 01. Apr 2017 16:45 Titel: Spezifische Wärme von Gasen (Legendre Transformation) |
 |
|
Hi,
kann mir vielleicht jemand etwas auf die Sprünge helfen bei der Aufgabe (Anhang)?
Zur a): Es gilt offensichtlich
 und und 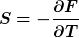 . .
Aber woran erkennt man nun wovon p und S abhängen?
zur c): Hier fehlt mir leider der Ansatz, kann mir jemand einen Tip geben wie ich vorgehen kann?
zur d): Siehe Anhang 2, ist das so richtig? Kommt mir irgendwie zu einfach vor..
Danke!
| Beschreibung: |
|

Download |
| Dateiname: |
4d Ansatz.png |
| Dateigröße: |
430.36 KB |
| Heruntergeladen: |
187 mal |
| Beschreibung: |
|

Download |
| Dateiname: |
Waerme.png |
| Dateigröße: |
589.47 KB |
| Heruntergeladen: |
202 mal |
|
|
 |
Neutrinowind
Anmeldungsdatum: 01.04.2017
Beiträge: 29
|
 Neutrinowind Verfasst am: 01. Apr 2017 19:35 Titel: Neutrinowind Verfasst am: 01. Apr 2017 19:35 Titel: |
 |
|
zu a)
Von welchen Größen hängt denn die freie Energie ab?
zu c)
Betrachte mal das totale Differential von
)
zu d)
Betrachte nochmal den Ausdruck aus der Aufgabe c). Wo steht dort ein Minuszeichen?
|
|
 |
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
|
 |
Neutrinowind
Anmeldungsdatum: 01.04.2017
Beiträge: 29
|
 Neutrinowind Verfasst am: 01. Apr 2017 23:27 Titel: Neutrinowind Verfasst am: 01. Apr 2017 23:27 Titel: |
 |
|
| Amateurphysiker hat Folgendes geschrieben: | Hi, danke!
zu a) also F hängt von T und V ab, aber was impliziert das für S und p?
|
Wenn du eine Funktion von T und V hast, von welchen Variablen hängt dann die Ableitung dieser Funktion nach T bei konstantem V bzw. nach V bei konstantem T ab?
| Zitat: |
zu b) Ich hänge leider immer noch. Also das Totale Differenzial wäre ja
=\frac{\partial S}{\partial T}dt+\frac{\partial S}{\partial V}dV )
Aber wie komme ich damit weiter?
|
Überlege dir mal wie man ausgehend von diesem Differential auf

kommt. Das ist ein wichtiger Zwischenschritt und damit bist du schon fast am Ziel.
| Zitat: |
zu c) Ups ok da hab ich was vertauscht. Stimmt es so? (Anhang) |
Ja. Du kannst aber dein Ergebnis noch vereinfachen.
|
|
 |
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
 Amateurphysiker Verfasst am: 02. Apr 2017 15:46 Titel: Amateurphysiker Verfasst am: 02. Apr 2017 15:46 Titel: |
 |
|
Danke! :-)
Also zu a) d.h. p=p(T) und S=S(V) oder?
zu c) ok danke, also dann c_p-c_V=nR?
zu b) ok aber dann muss ich erstmal irgendwie an S(T,p) rankommen oder? D.h. ich müsste S(T,V) nach p legendre-transformieren?
Aber es ist ja }{\partial V} ) . Mir fehlt der Zusammenhang von S und p um zu transformieren!? . Mir fehlt der Zusammenhang von S und p um zu transformieren!?
Danke!
|
|
 |
Neutrinowind
Anmeldungsdatum: 01.04.2017
Beiträge: 29
|
 Neutrinowind Verfasst am: 02. Apr 2017 16:38 Titel: Neutrinowind Verfasst am: 02. Apr 2017 16:38 Titel: |
 |
|
| Amateurphysiker hat Folgendes geschrieben: | Danke! :-)
Also zu a) d.h. p=p(T) und S=S(V) oder?
|
Betrachten wir als Beispiel die Funktion =x^2y^3) . .
Von welchen Variablen hängt die Ableitung dieser Funktion nach x bei konstantem y ab?
| Zitat: |
zu c) ok danke, also dann c_p-c_V=nR?
|
Ja das ist richtig.
| Zitat: | zu b) ok aber dann muss ich erstmal irgendwie an S(T,p) rankommen oder? D.h. ich müsste S(T,V) nach p legendre-transformieren?
Aber es ist ja }{\partial V} ) . Mir fehlt der Zusammenhang von S und p um zu transformieren!? . Mir fehlt der Zusammenhang von S und p um zu transformieren!? |
Wenn du ) einer legendre-transformation unterziehst, hast du nicht mehr die Entropie, sondern ein anderes thermodynamisches Potential. einer legendre-transformation unterziehst, hast du nicht mehr die Entropie, sondern ein anderes thermodynamisches Potential.
Mir ist im Moment nicht klar woran es bei dir hapert. Hast du die Gleichung, die ich hingeschrieben habe, verstanden und wenn ja weißt du wie man darauf kommt?
|
|
 |
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
 Amateurphysiker Verfasst am: 02. Apr 2017 17:22 Titel: Amateurphysiker Verfasst am: 02. Apr 2017 17:22 Titel: |
 |
|
| Neutrinowind hat Folgendes geschrieben: |
Betrachten wir als Beispiel die Funktion =x^2y^3) . .
Von welchen Variablen hängt die Ableitung dieser Funktion nach x bei konstantem y ab? |
Ups :-) Ok also die Ableitung nach x hängt immer noch von x und y ab!?
| Zitat: | Wenn du ) einer legendre-transformation unterziehst, hast du nicht mehr die Entropie, sondern ein anderes thermodynamisches Potential. einer legendre-transformation unterziehst, hast du nicht mehr die Entropie, sondern ein anderes thermodynamisches Potential.
Mir ist im Moment nicht klar woran es bei dir hapert. Hast du die Gleichung, die ich hingeschrieben habe, verstanden und wenn ja weißt du wie man darauf kommt? |
Also ich verstehe, dass
(Gleichung 2) 
die Gleichung ist, die gezeigt werden soll (da del S/del V = del p/del T).
Was ich nicht verstehe ist a) wie ich von
(Gleichung 1) =\frac{\partial S}{\partial T}dt+\frac{\partial S}{\partial V}dV )
auf

komme und b) wie ich S(T,p) bestimme (um dann davon die partielle Ableitung zu bilden).
Danke!
|
|
 |
Neutrinowind
Anmeldungsdatum: 01.04.2017
Beiträge: 29
|
 Neutrinowind Verfasst am: 02. Apr 2017 18:19 Titel: Neutrinowind Verfasst am: 02. Apr 2017 18:19 Titel: |
 |
|
| Amateurphysiker hat Folgendes geschrieben: |
Ups :-) Ok also die Ableitung nach x hängt immer noch von x und y ab!?
|
genau und was bedeutet das jetzt für die Aufgabe?
| Zitat: |
Was ich nicht verstehe ist a) wie ich von
(Gleichung 1) =\frac{\partial S}{\partial T}dt+\frac{\partial S}{\partial V}dV )
auf

komme und b) wie ich S(T,p) bestimme (um dann davon die partielle Ableitung zu bilden).
Danke! |
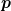 ist eine Funktion von ist eine Funktion von 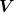 . Das heißt du kannst die Funktion nach V auflösen und in S(T, V) einsetzen, um S(T, p) zu erhalten. Es ist S(T, V)=S(T, p). Einmal drückst du die Entropie mit der Temperatur und dem Volumen aus und ein andermal mit der Temperatur und dem Druck, dennoch ist es in beiden Situationen dieselbe Funktion. . Das heißt du kannst die Funktion nach V auflösen und in S(T, V) einsetzen, um S(T, p) zu erhalten. Es ist S(T, V)=S(T, p). Einmal drückst du die Entropie mit der Temperatur und dem Volumen aus und ein andermal mit der Temperatur und dem Druck, dennoch ist es in beiden Situationen dieselbe Funktion.
|
|
 |
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
 Amateurphysiker Verfasst am: 02. Apr 2017 18:35 Titel: Amateurphysiker Verfasst am: 02. Apr 2017 18:35 Titel: |
 |
|
| Neutrinowind hat Folgendes geschrieben: |
genau und was bedeutet das jetzt für die Aufgabe? |
Ok dann ist es klar :-) p und S hängen (genauso wie F) von T und V ab.
| Zitat: | 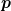 ist eine Funktion von ist eine Funktion von 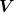 . Das heißt du kannst die Funktion nach V auflösen und in S(T, V) einsetzen, um S(T, p) zu erhalten. Es ist S(T, V)=S(T, p). Einmal drückst du die Entropie mit der Temperatur und dem Volumen aus und ein andermal mit der Temperatur und dem Druck, dennoch ist es in beiden Situationen dieselbe Funktion. . Das heißt du kannst die Funktion nach V auflösen und in S(T, V) einsetzen, um S(T, p) zu erhalten. Es ist S(T, V)=S(T, p). Einmal drückst du die Entropie mit der Temperatur und dem Volumen aus und ein andermal mit der Temperatur und dem Druck, dennoch ist es in beiden Situationen dieselbe Funktion. |
Ähm sorry, ich sitz auf dem Schlauch. Was kann ich nach V auflösen? Gleichung 1??
|
|
 |
Neutrinowind
Anmeldungsdatum: 01.04.2017
Beiträge: 29
|
 Neutrinowind Verfasst am: 02. Apr 2017 23:21 Titel: Neutrinowind Verfasst am: 02. Apr 2017 23:21 Titel: |
 |
|
| Amateurphysiker hat Folgendes geschrieben: |
Ähm sorry, ich sitz auf dem Schlauch. Was kann ich nach V auflösen? Gleichung 1?? |
p ist eine Funktion von V, als es ist p=p(V). den genauen funktionalen Zusammenhang kennst du nicht, bzw musst du nicht kennen. Wichtig ist nur, dass es diese Abhängigkeit gibt. Ein Beispiel wäre das ideale Gas. In dem Fall wäre der Zusammenhang durch p(V)=nRT/V gegeben.
Weiterhin betrachtest du eine Funktion S(T, V), aber du willst die Funktion in Abhängigkeit von T und p haben, also S(T, p). Da jedoch p=p(V), ist auch V=V(p).
Also S(T, V)=S(T, V(p))= S(T, p). Wenn V von p abhängt, hängt S(T, V) logischerweise bereits von p ab. Du musst also lediglich V durch p ersetzen.
Ist es jetzt klarer geworden?
|
|
 |
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
 Amateurphysiker Verfasst am: 03. Apr 2017 15:02 Titel: Amateurphysiker Verfasst am: 03. Apr 2017 15:02 Titel: |
 |
|
Hey vielen Dank, dass du dir die Zeit nimmst mir das zu erklären! Leider hab ich es immer noch nicht ganz kapiert.
| Neutrinowind hat Folgendes geschrieben: |
p ist eine Funktion von V, als es ist p=p(V). den genauen funktionalen Zusammenhang kennst du nicht, bzw musst du nicht kennen. Wichtig ist nur, dass es diese Abhängigkeit gibt. Ein Beispiel wäre das ideale Gas. In dem Fall wäre der Zusammenhang durch p(V)=nRT/V gegeben.
Weiterhin betrachtest du eine Funktion S(T, V), aber du willst die Funktion in Abhängigkeit von T und p haben, also S(T, p). Da jedoch p=p(V), ist auch V=V(p). |
Ok soweit kann ich folgen.
| Zitat: |
Also S(T, V)=S(T, V(p))= S(T, p). |
Was bedeutet diese Gleichung genau? Dass S sowohl eine Funktion von T und V als auch von T und p ist (ohne genauer auf den Zusammenhang einzugehen)?
| Zitat: |
Wenn V von p abhängt, hängt S(T, V) logischerweise bereits von p ab. Du musst also lediglich V durch p ersetzen.
|
Also dann kann ich
=\frac{\partial S}{\partial T}\bigg |_VdT+\frac{\partial S}{\partial V}\bigg |_TdV ) (Gleichung 1) (Gleichung 1)
schreiben als
=\frac{\partial S}{\partial T}\bigg |_pdT+\frac{\partial S}{\partial p}\bigg |_Tdp ) (Gleichung 2) (Gleichung 2)
Aber wie komme ich damit auf
 (Gleichung 3) (Gleichung 3)
? Das ist mir leider noch nicht klar..
Gilt denn (1)=(2)?
Falls ja, dann würde folgen, dass
 (Gleichung 4) (Gleichung 4)
Stimmt das? Und falls ja, wie komme ich von (4) auf (3)?
Danke!!
|
|
 |
|















