| Autor |
Nachricht |
gnt
Gast
|
 gnt Verfasst am: 16. Jan 2017 18:48 Titel: Spin und Pauli-Gleichung gnt Verfasst am: 16. Jan 2017 18:48 Titel: Spin und Pauli-Gleichung |
 |
|
Hallo allerseits,
beim Lesen und Verstehen versuchen der Pauli-Gleichung habe ich ein Problem; evtl. nur mit der Notation. Ich schaue gerade auf Wikipedia https://de.wikipedia.org/wiki/Pauli-Gleichung die erste Gleichung an.
Wenn ich das richtig sehe, ist auf der rechten Seite der Gleichung der erste Term skalar, aber im zweiten Term wirkt eine Matrix auf die beiden Wellenfunktionen für spin-up und spin-down und dadurch werden die beiden Funktionen gekoppelt. Richtig?
Wenn aber 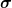 für für  steht, dann würde diese Kopplung nur bei Magnetfeldern mit x- und y-Anteil wirken. Bei Feldern rein in z-Richtung findet keine Kopplung statt. Fehlt in der Gleichung ein Vektor für die Spinrichtung? steht, dann würde diese Kopplung nur bei Magnetfeldern mit x- und y-Anteil wirken. Bei Feldern rein in z-Richtung findet keine Kopplung statt. Fehlt in der Gleichung ein Vektor für die Spinrichtung?
Kann man die beiden Gleichungen auch entkoppeln?
Schon 'mal Vielen Dank für die Erklärung!
Gruss
gnt |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 16. Jan 2017 19:34 Titel: TomS Verfasst am: 16. Jan 2017 19:34 Titel: |
 |
|
Der linke bzw. der rechte Term sind wie folgt zu lesen:
^2 \right] + q\Phi\right)\,(1)_{ab}\,\phi_b)
_{ab}\right] \,\phi_b )
Verstehst du diese Indexstruktur?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
gnt
Gast
|
 gnt Verfasst am: 16. Jan 2017 21:28 Titel: gnt Verfasst am: 16. Jan 2017 21:28 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Verstehst du diese Indexstruktur? |
Ja.
Wenn a=1=spin-up und a=2=spin-down bedeutet, habe ich das so gelesen.
Aber dann trifft doch das zu, was ich oben vermutet habe, nämlich, dass die Spin-Richtung in der Gleichung fehlt. Der Spin hat doch wie der Drehimpuls eine Richtung. Oder ist das vom Prinzip her das gleiche Problem, das ich mit der Schrödingergleichung hatte, also dass die Pauli-Gleichung die Spinausrichtung gar nicht festlegt, sondern nur allgemeine Lösungen liefert? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 16. Jan 2017 21:57 Titel: TomS Verfasst am: 16. Jan 2017 21:57 Titel: |
 |
|
Genauso ist das.
Die Spinausrichtung steckt nicht in der Gleichung sondern in der Lösung phi.
Wenn kein Magnetfeld herrscht, also B = 0, dann ist der Kopplungsterm Null. Damit entkoppeln die beiden Spinkomponenten und entwickeln sich unabhängig voneinander. Wenn ein Magnetfeled herrscht, dann gilt dies nicht mehr.
Eine eindeutige Spinausrichtung liegt dann vor, wenn phi ein Eigenzustand zu einem Spinoperator ist. Dieser ist allgemein definiert als Linearkombination
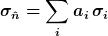
wobei die Koeffizienten a mit dem Vektor n zusammenhängen, der eine allgemeine Richtung im Raum definiert. Dies entspricht im wesentlichen einer Drehung der räumlichen Einheitsvektoren, die gleichzeitig eine Drehung der Spinmatrizen induziert.
Eine eindeutige Spinausrichtung bzgl. der Richtung n liegt vor, wenn man ein derartiges n finden kann, so dass
 \, \phi_\pm = 0)
gilt.
Wählt man die z-Richtung geeignet parallel zu n, dann ist dies einfach
 \, \phi_\pm = 0)
mit
 |
|
 |
gnt
Gast
|
 gnt Verfasst am: 16. Jan 2017 23:31 Titel: gnt Verfasst am: 16. Jan 2017 23:31 Titel: |
 |
|
Gut, Danke!
Aber was bedeutet diese Kopplung? Ist das nur ein Rechentrick, der etwas vereinfacht, oder bedeutet das, dass (bei B!=0) die beiden Funktionen für spin up und down nur gemeinsam sowohl existieren als auch zeitlich entwickeln können? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 17. Jan 2017 00:19 Titel: TomS Verfasst am: 17. Jan 2017 00:19 Titel: |
 |
|
Die Möglichkeit der Existenz von diesen Spinoren folgt aus der Geometrie der Raumzeit gem. SRT. Die Notwendigkeit folgt aus der Tatsache, dass Spin nur so mathematisch beschrieben werden kann.
Die Pauli-Gleichung ist lediglich eine nicht-rel. Näherung der Dirac-Gleichung und verschleiert deren zugrundeliegende mathematische Struktur
\,\psi = 0)

Der Diracgleichung-Spinor psi ist eine 4-komponentiger Bispinor. Man erkennt dass im nicht-rel. Grenzfall zwei Komponenten "klein" sind und kann eine systematische Entwicklung durchführen. Daraus resultiert dann die Pauli-Gleichung für den verbleibenden 2-komponentigen Spinor phi.
Diese Spinoren müssen für Teilchen mit Spin immer verwendet werden; für B = 0 ist die resultierende Gleichung jedoch einfach, da die beiden Komponenten unabhängig sind und letztlich zwei ungekoppelte Gleichungen für die beiden Komponenten von phi resultieren. |
|
 |
gnt
Gast
|
 gnt Verfasst am: 17. Jan 2017 11:43 Titel: gnt Verfasst am: 17. Jan 2017 11:43 Titel: |
 |
|
Bedeutet das letztlich, dass ein Teilchen in einem Spinzustand, das nur durch eine einzige Wellenfunktion beschrieben wird, stets auch von den Funktionen der anderen drei Teilchen, die existieren könnten, beeinflusst wird? - Das gefällt mir nicht. ;-)
| TomS hat Folgendes geschrieben: | | Die Pauli-Gleichung ist lediglich eine nicht-rel. Näherung der Dirac-Gleichung und verschleiert deren zugrundeliegende mathematische Struktur |
Ist es also eher sinnlos zu versuchen, die Pauli-Gleichung zu verstehen? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 17. Jan 2017 12:17 Titel: TomS Verfasst am: 17. Jan 2017 12:17 Titel: |
 |
|
| gnt hat Folgendes geschrieben: | | Bedeutet das letztlich, dass ein Teilchen in einem Spinzustand, das nur durch eine einzige Wellenfunktion beschrieben wird, stets auch von den Funktionen der anderen drei Teilchen, die existieren könnten, beeinflusst wird? - Das gefällt mir nicht. ;-) |
Hast du ein Glück, so ist es nämlich auch nicht :-)
Es gibt nur genau ein Teilchen mit einer Wellenfunktion, aber die hat zwei Komponenten (vgl. el.-mag. Feld; da reicht auch nicht eine Komponente aus) Und wie kommst du auf drei?
| gnt hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Die Pauli-Gleichung ist lediglich eine nicht-rel. Näherung der Dirac-Gleichung und verschleiert deren zugrundeliegende mathematische Struktur |
Ist es also eher sinnlos zu versuchen, die Pauli-Gleichung zu verstehen? |
Nein, ist es nicht. Die Frage ist, was du tun möchtest.
Wenn du einen Einstieg in die Spinalgebra suchst und konkrete physikalische Anwendungen diskutieren möchtest, dann ist die Pauli-Gleichung sehr gut geeignet. Ein interessanter erster Ansatz ist, den kinetischen Term für sehr große m also für sehr kleine 1/2m zu vernachlässigen und lediglich
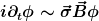
für homogenens und konstantes

zu betrachten.
Wenn du dagene lernen möchtest, wie der Spin mit der Lorentzgruppe und der Raumzeit zusammenhängt, dann solltest du die Dirac-Gleichung betrachten. |
|
 |
gnt
Gast
|
 gnt Verfasst am: 17. Jan 2017 13:40 Titel: gnt Verfasst am: 17. Jan 2017 13:40 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Hast du ein Glück, so ist es nämlich auch nicht :-) |
Jetzt bin ich beruhigt.
| TomS hat Folgendes geschrieben: | | Es gibt nur genau ein Teilchen mit einer Wellenfunktion, aber die hat zwei Komponenten (vgl. el.-mag. Feld; da reicht auch nicht eine Komponente aus) |
Gut.
Demnach war Diracs Erkenntnis bzgl. der Existenz von Antiteilchen kein einfaches Abzählen der Gleichungen...
| TomS hat Folgendes geschrieben: | | Und wie kommst du auf drei? |
Ich habe mich auf die Dirac-Gleichung bezogen, also Antiteilchen mitgerechnet - eine Funktion des Teilchens plus drei andere.
| TomS hat Folgendes geschrieben: | | Die Frage ist, was du tun möchtest. |
Eigentlich würde ich gerne die Struktur der QED verstehen, weil wohl nur so der ganze Apparat mit Relativität, geladenen Teilchen incl. Spin und Photonen ein schlüssiges System ergibt. Dabei liegt die Betonung auf "Struktur" und "verstehen". Dass konkrete Rechnung extrem kompliziert sind, ist mir klar, aber "nur" rechnen, oder "nur" Feynman-Regeln abzuarbeiten empfinde ich als eher unbefriedigend.
Die Pauli-Gleichung habe ich angesehen, weil der Sprung von der Schrödingergleichung nicht so gross ist, und die Dirac-Gleichung schon recht unübersichtlich ist. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 17. Jan 2017 15:09 Titel: TomS Verfasst am: 17. Jan 2017 15:09 Titel: |
 |
|
| gnt hat Folgendes geschrieben: | | Ich habe mich auf die Dirac-Gleichung bezogen, also Antiteilchen mitgerechnet - eine Funktion des Teilchens plus drei andere. |
Nach moderner Lesart kommt man auf die Antiteilchen, in dem man den die Ladungskonjugation anwendet und
| gnt hat Folgendes geschrieben: | | Eigentlich würde ich gerne die Struktur der QED verstehen, weil wohl nur so der ganze Apparat mit Relativität, geladenen Teilchen incl. Spin und Photonen ein schlüssiges System ergibt. Dabei liegt die Betonung auf "Struktur" und "verstehen". Dass konkrete Rechnung extrem kompliziert sind, ist mir klar, aber "nur" rechnen, oder "nur" Feynman-Regeln abzuarbeiten empfinde ich als eher unbefriedigend. |
Verstehe ich, aber auch "nur die Struktur verstehen" ist ein haufen Arbeit.
| gnt hat Folgendes geschrieben: | | Die Pauli-Gleichung habe ich angesehen, weil der Sprung von der Schrödingergleichung nicht so gross ist, und die Dirac-Gleichung schon recht unübersichtlich ist. |
Die Dirac-Gleichung wäre aber der Einstieg in die QED ... |
|
 |
|
|















