| Autor |
Nachricht |
merlot0001
Gast
|
 merlot0001 Verfasst am: 06. Feb 2016 17:17 Titel: Lagrangefunktion - Gewicht am Seil merlot0001 Verfasst am: 06. Feb 2016 17:17 Titel: Lagrangefunktion - Gewicht am Seil |
 |
|
Meine Frage:
Hallo,
ich möchte die Lagrange-Funktion zu folgendem Problem aufstellen. Außerdem soll die L-Funktion nur von einer generalisierten Koordinate abhängen:
http://i.imgur.com/yE6pjCH.jpg?1
Zu der kinetischen Energie des Gewichts kommt außerdem noch die kinetische Energie  hinzu. hinzu.
Meine Ideen:
Die Rotationsachse der Kugel lege ich in z-Richtung. Das Seil velräuft parallel zur y-Achse.
Also wäre die potentielle Energie des Gewichtes:
U = m g y
Da die Rotationsenergie den Winkel  enthält und die Aufgabe fordert, dass allein eine generalisierte Koordiante eingeführt wird, würde ich enthält und die Aufgabe fordert, dass allein eine generalisierte Koordiante eingeführt wird, würde ich 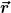 des Gewichts irgendwie über den Winkel des Gewichts irgendwie über den Winkel 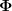 ausdrücken. ausdrücken.
Weiß aber nicht wie....
Danke! |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 06. Feb 2016 17:28 Titel: franz Verfasst am: 06. Feb 2016 17:28 Titel: |
 |
|
Eine andere Möglichkeit wäre die Höhe.
Vielleicht aber erstmal den Kugelradius r (über m und J). |
|
 |
Duncan
Gast
|
 Duncan Verfasst am: 06. Feb 2016 17:32 Titel: Re: Lagrangefunktion - Gewicht am Seil Duncan Verfasst am: 06. Feb 2016 17:32 Titel: Re: Lagrangefunktion - Gewicht am Seil |
 |
|
| merlot0001 hat Folgendes geschrieben: | 
|
Allein schon die Betrachtung der Einheiten zeigt, dass diese Gleichung keinen Sinn ergibt. |
|
 |
merlot0001
Gast
|
 merlot0001 Verfasst am: 06. Feb 2016 17:33 Titel: merlot0001 Verfasst am: 06. Feb 2016 17:33 Titel: |
 |
|
Das verstehe ich nicht..
Der Kugelradius wird konstant sein.
Und ich will die Lagrange-Funktion zu diesem System aufstellen.

Und diese Lagrange-Funktion soll durch eine einzige generalisierte Koordinate ausgedrückt werden!
Ich hätte aber für die Masse m sowas wie ^T) gewählt... gewählt...
Und wie ich y über den Winkel (falls das überhaupt die generalisierte Koordinate sein soll) ausdrucken soll, ist mir schleierhaft.
Hättest du Lust deine Idee etwas auszuführen? Vielen Dank |
|
 |
merlot0001
Gast
|
 merlot0001 Verfasst am: 06. Feb 2016 17:36 Titel: merlot0001 Verfasst am: 06. Feb 2016 17:36 Titel: |
 |
|
Es steht nichts näher dabei; aber ich denke, dass es die Winkelgeschwindigkeit ist.
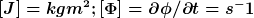
Also passt das schon so.. |
|
 |
merlot0001
Gast
|
 merlot0001 Verfasst am: 06. Feb 2016 17:39 Titel: merlot0001 Verfasst am: 06. Feb 2016 17:39 Titel: |
 |
|
Hier nochmal die Aufgabe inklusive Aufgabenteile:
i.imgur.com/HflSCRa.jpg |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 06. Feb 2016 17:43 Titel: franz Verfasst am: 06. Feb 2016 17:43 Titel: |
 |
|
|
Für den Zusammenhang zwischen Höhe und Drehwinkel benötigst Du den Kugelradius r = r(m,J). |
|
 |
Duncan
Gast
|
 Duncan Verfasst am: 06. Feb 2016 17:58 Titel: Duncan Verfasst am: 06. Feb 2016 17:58 Titel: |
 |
|
| merlot0001 hat Folgendes geschrieben: |
 Also passt das schon so.. Also passt das schon so.. |
Ja das ist richtig.
Aber 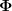 ist dann aber kein Winkel, wie behauptet. ist dann aber kein Winkel, wie behauptet.
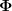 ist die Winkelgeschwindigkeit! ist die Winkelgeschwindigkeit!
Üblich ist es, sie mit  zu bezeichnen. zu bezeichnen. |
|
 |
merlot0001
Gast
|
 merlot0001 Verfasst am: 06. Feb 2016 18:03 Titel: merlot0001 Verfasst am: 06. Feb 2016 18:03 Titel: |
 |
|
@Duncan: Sorry, die Kopie ist leider etwas schlecht; evtl. steht dort auch sowas wie 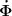 . Kann es leider nicht sehen . Kann es leider nicht sehen
@franz: Kugel: 
Aber wie soll ich denn so die Höhe des Gewichtes über den KUGELRADIUS r bestimmen und dessen Drehwinkel? |
|
 |
merlot0001
Gast
|
 merlot0001 Verfasst am: 06. Feb 2016 18:10 Titel: merlot0001 Verfasst am: 06. Feb 2016 18:10 Titel: |
 |
|

Das Stück "y" das hinzukommt, ist genau die Länge des Kreisbogens b.

Also 
somit wäre der Ortsvektor des MP ^T)
Macht das.. Sinn...? |
|
 |
Duncan
Gast
|
 Duncan Verfasst am: 06. Feb 2016 18:13 Titel: Duncan Verfasst am: 06. Feb 2016 18:13 Titel: |
 |
|
Du musst zuerst festlegen, was deine generalisierte Koordinate ist.
Es bietet sich an
entweder x, der Weg, den das Gewicht zurücklegt
oder  , der Winkel um den sich die Kugel dreht. , der Winkel um den sich die Kugel dreht.
Dann stellst du kinetische und potentielle Energie als Funktion dieser Koordinate auf. |
|
 |
Duncan
Gast
|
 Duncan Verfasst am: 06. Feb 2016 18:16 Titel: Duncan Verfasst am: 06. Feb 2016 18:16 Titel: |
 |
|
| merlot0001 hat Folgendes geschrieben: | 
Macht das.. Sinn...? |
Nein.
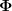 ist doch die Winkelgeschwindigkeit. ist doch die Winkelgeschwindigkeit. |
|
 |
merlot0001
Gast
|
 merlot0001 Verfasst am: 06. Feb 2016 18:20 Titel: merlot0001 Verfasst am: 06. Feb 2016 18:20 Titel: |
 |
|
dann revidiere ich das von vorhin und definiere es jetzt so


Macht es dann so Sinn?
L würde dann nur noch von $\Phi$ bzw. $\dot{\Phi}$ abhängen |
|
 |
Duncan
Gast
|
 Duncan Verfasst am: 06. Feb 2016 18:38 Titel: Duncan Verfasst am: 06. Feb 2016 18:38 Titel: |
 |
|
| merlot0001 hat Folgendes geschrieben: |

Macht es dann so Sinn?
L würde dann nur noch von $\Phi$ bzw. $\dot{\Phi}$ abhängen |
Also für mich ergibt dies keinen Sinn.
Was ist L ? |
|
 |
merlot0001
Gast
|
 merlot0001 Verfasst am: 06. Feb 2016 18:56 Titel: merlot0001 Verfasst am: 06. Feb 2016 18:56 Titel: |
 |
|
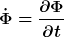
L soll die Lagrange-Funktion sein.

Hierbei ist T die kinetische Energie und U die potentielle Energie!
Könntest Du mir den Term für die kinetische Energie T aufschreiben? Du würdest mir damit wirklich gewaltig helfen. Da ich nicht weiß, wie ich dieses Problem soll.
Und danke auch, dass du wirklich jeden Fehler einzeln kommentierst und ihn mich korrigieren lässt. Nur so werde ich es wirklich lernen. Diese Hilfsbereitschaft ist nicht selbstverständlich. |
|
 |
merlot0001
Gast
|
 merlot0001 Verfasst am: 06. Feb 2016 19:04 Titel: merlot0001 Verfasst am: 06. Feb 2016 19:04 Titel: |
 |
|
Ups! Wahrscheinlich zu ungenau :-).
Den Term für die kinetische Energie auf diese Aufgabe bezogen (s. 1. Posting bzw. weiter unten ein zweiter Upload der Aufgabenstellung).
Des Weiteren sollte die Funktion L (s. Posting 06. Feb 2016 18:56) nur von einer generalisierten Koordinate abhängen.
Wenn ich die Potentielle Energie U so definiere 
(Ja, ich weiß: Ich habe es vorhin anders definiert, aber ab diesem Posting(!) liegt die x-Achse parallel zum Seil und zeigt in Richtung Gewicht m. Grund: Aufgabenteil c) suggeriert mir, dass es sich so ohne Änderung der Achsen weiterrechnen ließe.)
Du und franz hatten angedeutet, dass man das ganze Probleme auch über die generalisierte Koordinate "x" ausdrücken kann. Wie sähe die Funktion L (L=Lagrange-Fkt.) dann aus? |
|
 |
Duncan
Gast
|
 Duncan Verfasst am: 06. Feb 2016 19:27 Titel: Duncan Verfasst am: 06. Feb 2016 19:27 Titel: |
 |
|
Gewählte Koordinate = x, der Weg, den das Gewicht zurücklegt.
(positiv nach unten).
dann ist
Gewicht:


Kugel:
U = 0

wobei
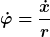
r ist ja bekannt (Kugelradius) |
|
 |
merlot0001
Gast
|
 merlot0001 Verfasst am: 06. Feb 2016 19:43 Titel: merlot0001 Verfasst am: 06. Feb 2016 19:43 Titel: |
 |
|
Habe in einem Lehrbuch eine vergleichbare Aufgabe gefunden.
Mit der Zwangsbedingung  kommt man schnell zur Lösung. kommt man schnell zur Lösung.
Damit folgt 
Das eingesetzt in die Rotationsenergie liefert:
 \right)\dot{x}^2)
und )
Danke für deine Mühe Duncan.. und.. ach, vergiss es.
btw: "Mal-Punkt": $\cdot$
oder: Leertaste "\," bzw. (größere) "\;"
(diese Trennungen mit . sehen ja doch etwas verwirrend aus - ich wusste anfangs überhaupt nicht, was du meinst  ) )
Und wieso jetzt plötzlich  ? Ist das ein anderer Winkel? Aber ich bin (mit normalem Menschenverstand) davon ausgegangen, dass du ? Ist das ein anderer Winkel? Aber ich bin (mit normalem Menschenverstand) davon ausgegangen, dass du 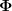 meintest! Einfach krass... diese... Transferleistung.... meintest! Einfach krass... diese... Transferleistung.... |
|
 |
|
















 )
)