| Autor |
Nachricht |
Baum03
Anmeldungsdatum: 15.11.2023
Beiträge: 1
|
 Baum03 Verfasst am: 15. Nov 2023 15:59 Titel: Masse am Seil Baum03 Verfasst am: 15. Nov 2023 15:59 Titel: Masse am Seil |
 |
|
Meine Frage:
Eine Masse M ist uber einen Faden der Länge l, der über
eine (kleine) Rolle geführt wird, mit einer Masse m verbunden. Die Masse m wird im Schwerefeld fallen gelassen. Bestimmen Sie die Lagrangefunktion des Problems nach Wahl geeigneter Koordinaten und
Berücksichtigung von Zwangsbedingungen. (Es wird angenommen, dass der Faden zu jedem Zeitpunkt aus zwei
geraden Verbindungsstucken zwischen den Massen und der Rolle besteht. Außerdem ist die Aufhängung an der
Rolle so, dass die beiden Massen und die Fäden aneinander vorbei schwingen können, ohne sich zu berühren.
Meine Ideen:
Ich bin etwas überfordert, wie ich das machen soll, in der Vorlesung haben wir Abrutschendes Seil und Kugelpendel gemacht, ich bräuchte hilfe. Ich hätte jetzt Kugelkordinaten gewählt, aber ich weiß nicht wie lang die Seile sind,
|
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 15. Nov 2023 20:04 Titel: Re: Masse am Seil DrStupid Verfasst am: 15. Nov 2023 20:04 Titel: Re: Masse am Seil |
 |
|
| Baum03 hat Folgendes geschrieben: | | Ich hätte jetzt Kugelkordinaten gewählt, aber ich weiß nicht wie lang die Seile sind, |
Kugelkoordinaten sind keine schlechte Wahl, obwohl es natürlich auch anders geht.
Da Abmessungen und Trägheitsmoment der Rolle nicht gegeben sind, würde ich sie der Einfachheit halber als punktförmig annehmen. Aber ohne zusätzlichen Kontext weiß ich aber nicht, ob das zulässig ist. Mit dieser Vereinfachung ergeben die Längen der beiden Seilstücke zusammen die Fadenlänge l. Die verbleibende Unbekannte ist dann eine der generalisierten Koordinaten.
Wenn der Radius der Rolle nicht vernachlässigbar ist, dann wird es deutlich komplizierter. In dem Fall helfen auch die Kugelkoordinaten nicht wirklich weiter.
Welche Parameter bräuchtest Du denn noch, um das Systeme eindeutig zu bestimmen?
|
|
 |
microsoft_AI
Gast
|
 microsoft_AI Verfasst am: 15. Nov 2023 23:36 Titel: microsoft_AI Verfasst am: 15. Nov 2023 23:36 Titel: |
 |
|
Die Lagrange-Funktion ist ein nützliches Werkzeug in der klassischen Mechanik und ermöglicht es uns, die Bewegung eines Systems zu beschreiben. In diesem Fall haben wir ein System mit zwei Massen, die durch einen Faden verbunden sind.
Wir können die Höhe der M-Masse als y und die Höhe der m-Masse als x bezeichnen. Da der Faden eine konstante Länge hat, gilt: x + y = l.
Die kinetische Energie T des Systems ist die Summe der kinetischen Energien der beiden Massen:
T=21My˙2+21mx˙2
Die potentielle Energie V des Systems ist die Summe der potentiellen Energien der beiden Massen im Schwerefeld:
V=Mgy−mgx
Die Lagrange-Funktion L ist definiert als die Differenz zwischen der kinetischen und der potentiellen Energie:
L=T−V=21My˙2+21mx˙2−Mgy+mgx
Da die Länge des Fadens konstant ist, haben wir eine Zwangsbedingung, die wir berücksichtigen müssen. Diese kann durch die Verwendung der Methode der Lagrange-Multiplikatoren oder durch die Wahl geeigneter Koordinaten berücksichtigt werden.
|
|
 |
izzy
Anmeldungsdatum: 28.10.2023
Beiträge: 18
|
 izzy Verfasst am: 16. Nov 2023 13:54 Titel: izzy Verfasst am: 16. Nov 2023 13:54 Titel: |
 |
|
Hallo, ich sitze gerade an einer ähnlichen Aufgabe und versuche die Antwort von microsoft_AI zu verstehen. Was meinst du mit 21( soll das ein halb sein)? soll das \frac{1}{2} sein?
T= \frac{1}{2} * M \dot{y} + \frac{1}{2} * M \dot{x}
(meinst du dass?)
Bei der Formel die microsoft_AI aufgestellt hat wird da überhaupt die Möglichkeit des Pendelns mit aufgenommen? ( das die Masse m x ja losgelassen werden kann ) und dann die Masse y (M) dann nach oben gezogen werden könnte.?
( und müsste es nicht V=Mgy+mgx sein?)
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 16. Nov 2023 14:06 Titel: Myon Verfasst am: 16. Nov 2023 14:06 Titel: |
 |
|
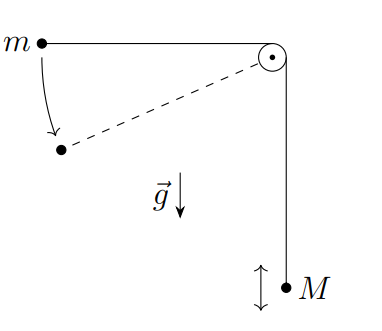
Gehört eigentlich eine Skizze zur Aufgabe? Können beide Massen frei in alle Richtungen Schwingen, oder nur die Masse m?
Wenn nur die eine Masse schwingen kann und sie sich nur in einer Ebene bewegt, also keinen Drehimpuls mitbekommt, reichen z.B. die Länge des Seils zwischen der Rolle und m sowie der Auslenkungswinkel als generalisierte Koordinaten.
|
|
 |
izzy
Anmeldungsdatum: 28.10.2023
Beiträge: 18
|
 izzy Verfasst am: 16. Nov 2023 14:15 Titel: izzy Verfasst am: 16. Nov 2023 14:15 Titel: |
 |
|
Ja es gehört ein Bild dazu, in diesem ist nichts von Rotation zu erkennen
| Beschreibung: |
|
| Dateigröße: |
9.57 KB |
| Angeschaut: |
2939 mal |
|
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 16. Nov 2023 14:58 Titel: Myon Verfasst am: 16. Nov 2023 14:58 Titel: |
 |
|
Dann versuch doch einmal, die Lagrangefunktion als Funktion der Länge l zwischen der Rolle und m und des Auslenkungswinkels phi aus der Vertikalen auszudrücken. Um einen Anfang zu machen: die kinetische Energie der Masse m wäre
)
Allerdings erhält man in den Bewegungsgleichungen auch eine Ableitung erster Ordnung nach der Zeit, und man kann nicht wie bei einem gekoppelten Pendel einfach Eigenfrequenzen berechnen.
|
|
 |
izzy
Anmeldungsdatum: 28.10.2023
Beiträge: 18
|
 izzy Verfasst am: 16. Nov 2023 15:23 Titel: izzy Verfasst am: 16. Nov 2023 15:23 Titel: |
 |
|
Das ist leider meine aller erste Lagrange Aufgabe und wir haben es auch gestern erst eingeführt bekommen, deshalb bin ich noch sehr unbeholfen.
das Passende V von m wäre dann V_1=m*g*loder ?
)
so in dierichtung?
|
|
 |
Qubit
Anmeldungsdatum: 17.10.2019
Beiträge: 851
|
 Qubit Verfasst am: 16. Nov 2023 16:13 Titel: Qubit Verfasst am: 16. Nov 2023 16:13 Titel: |
 |
|
Am Besten zeichnest du dir in das Bild mal ein Koordinatensystem ein.
Da es sich um Bewegungen in einer Ebene handelt, hast du dann mit Polarkoordinaten 4 Variablen:

Dazu kommen dann 2 Zwangsbedingungen, also bleiben 2 (generalisierte) Koordinaten.
Für die potentielle Energie bietet sich hier an, das Nullpotential in den Koordinatenursprung zu legen, so dass du negative Potentiale bekommst:

((  müsst du dir hier für die beiden Massen überlegen)) müsst du dir hier für die beiden Massen überlegen))
Wenn das klar ist, kannst du die Langrangefunktion aufschreiben:
 = T - V)
Zuletzt bearbeitet von Qubit am 16. Nov 2023 19:16, insgesamt einmal bearbeitet |
|
 |
izzy
Anmeldungsdatum: 28.10.2023
Beiträge: 18
|
|
 |
Qubit
Anmeldungsdatum: 17.10.2019
Beiträge: 851
|
 Qubit Verfasst am: 16. Nov 2023 19:27 Titel: Qubit Verfasst am: 16. Nov 2023 19:27 Titel: |
 |
|
Nun, du solltest lernen, systematischer an solche Aufgaben ranzugehen. 
In deinem Bild fehlt die Eintragung der Polarkoordinaten. (bitte nachholen)
Wenn du dies machst, dann stellen sich die beiden Zwangsbedingungen wie folgt dar:
 \, l_1 + l_2 = L \rightarrow \dot l_2 = - \dot l_1)
 \, \varphi_2 = 0 \rightarrow \dot \varphi_2 = 0)
Damit kannst du den kinetischen Energieterm formulieren.
Was dann die potentiellen Energien angeht, brauchen wir dann noch (allgemein unabhängig zur Wahl der y-Richtung formuliert):

Was ist dann hier  für die beiden Massen? für die beiden Massen?
|
|
 |
izzy
Anmeldungsdatum: 28.10.2023
Beiträge: 18
|
 izzy Verfasst am: 16. Nov 2023 21:57 Titel: izzy Verfasst am: 16. Nov 2023 21:57 Titel: |
 |
|
Es tut mir wirklich leid und ich stelle mich wirklich dumm an aber wie bekomme ich daraus die Kinetische energie? 
 wäre also eine zyklische Variabel wäre also eine zyklische Variabel
,)
)
Vom Verständnis her wäre dann
y= , ,  wäre wäre 
Bitte verbessere mich wenn ich falsch liege, es tut mir wirklich leid.
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 17. Nov 2023 10:20 Titel: Myon Verfasst am: 17. Nov 2023 10:20 Titel: |
 |
|
Zur kinetischen Energie: die Geschwindigkeit der Masse m hat eine Komponente in Richtung des Seils und eine Kompenente senkrecht dazu,

Für die Länge des Seils zwischen der Rolle und der Masse M gilt l2=L-l und damit

Damit wird die kinetische Energie
+\frac{M\dot{l}^2}{2})
Wählt man h=0 für die jeweils tiefstmögliche Position, gilt für die Höhen der Massen m und M

Die Addition einer Konstanten zur Lagrangefunktion ändert die resultierenden Bewegungsgleichungen nicht, konstante Terme können also weggelassen werden. Damit wird die Lagrange-Funktion
+\frac{M\dot{l}^2}{2}+mgl\cos\varphi-Mgl)
phi ist keine zyklische Koordinate.
|
|
 |
izzy
Anmeldungsdatum: 28.10.2023
Beiträge: 18
|
 izzy Verfasst am: 17. Nov 2023 10:52 Titel: izzy Verfasst am: 17. Nov 2023 10:52 Titel: |
 |
|
|
Vielen dank,
|
|
 |
|


















