| Autor |
Nachricht |
stk
Gast
|
 stk Verfasst am: 18. Feb 2006 12:50 Titel: Federpendel |
 |
|
Hi
Habe letzte woche einen test geschrieben und den total verhauen. Das dumme ist, dass ich kommende woche ne klausur über genau den gleichen mist schreibe.
Ich kann das wirklich überhaupt nicht, mein problem dabei sind vor allem die formeln.
Hier die Aufgabe aus dem Test:
Ein federpendel der masse m=600g wird aus seiner gleichgewichtslage um 8cm angehoben und dann losgelassen. Beim loslassen liegt der zeitnullpunkt. Die federkonstante beträgt D=1,20N/cm.
a) berechnen sie die auslenkung zum zeitpunkt t=0,15s
b) berechnen sie die maximale geschwindigkeit des federpendels
----
Gut, dazu habe ich 3 fragen erstmal zu der aufgabenstellung.
Was ist die gleichgewichtslage ? Es ist doch der punkt an dem das federpendel quasi stehen bleibt, gleichen sich da die kraft die nach unten wirkt und die kraft die vom federpendel ausgeht und nach oben wirkt aus ?
wenn das pendel um 8cm angehoben wird, ist das dann schon meine amplitude ?
Zeitnullpunkt - was hat das für mich zu bedeuten ?
---
Die rechnung habe ich natürlich total versaut... ich weiss nichtmal mehr wie ich auf den ganzen schrott gekommen bin, den ich da geschrieben habe.
Kann mir vielleicht jemand diese aufgabe ausrechnen und erläutern warum er was und wie einsetzt ? Wäre echt eine super hilfeleistung, ich muss erst immer einmal sehen wie es geht um das dann übertragen zu können.
vielen dank im voraus !
stk
|
|
 |
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
| as_string Verfasst am: 18. Feb 2006 13:36 Titel: |
|
|
Hallo!
Alles dreht sich ja um die Bewegungsgleichungen für einen harmonischen Oszillator:
 = A \sin{\left(\omega t + \varphi\right)})
 = A \omega \cos{\left(\omega t + \varphi\right)})
 = - A \omega^2 \sin{\left(\omega t + \varphi\right)})
mit
Das nur mal als Basis. Das ist sicher auch in Deinem Physikbuch drin, etc.
Jetzt zu Deinen speziellen Fragen:
Gleichgewichtslage: Das ist der Punkt, an dem keine (effektive) Kraft auf die Masse wirkt, an der Stelle wird die Masse also nicht beschleunigt. Allerdings: Das bedeutet nicht, dass sie sich da nicht bewegt! Sie kann ja eine Geschwindigkeit schon vorher haben, die sich in dem Punkt dann nicht ändert, weil ja ohne Kraft auch keine Beschleunigung existiert. Bei einer Schwingung ist die Masse an dem Punkt sogar am schnellsten! Die Geschwindigkeit wird nur =0 in den beiden Umkehrpunkten.
Wenn das Pendel allerdings nicht pendelt/schwingt, dann befindet es sich genau in dieser Position im Gleichgewicht und in Ruhe.
Die 8cm sind in diesem Fall Deine Amplitude, weil es dort, so wie ich die Aufgabe verstehe, aus der Ruhe losgelassen wird. Ich habe auch schon Aufgaben gesehen, bei dem es nicht aus der Ruhe, sondern mit einer Anfangsgeschwindigkeit anfängt. Dann wird das alles etwas komplizierter, weil man dann zu Beginn noch nicht mal die Amplitude direkt gegeben hat!
Für Deine Aufgabe ist also schon mal die Amplitude gegeben und  hast Du auch schon, weil ja die Masse m und die Federhärte D auch schon gegeben ist. Jetzt fehlt nur noch der Phasenwinkel  . Den kannst Du z. B. rausbekommen, wenn Du die Gleichung für s(t) nimmst und erstmal einsetzt. Ach ja, da wird vielleicht auch klar, warum da was mit t=0 in der Aufgabe steht, weil ich kann dann das hier schreiben:
 = 8\text{cm} = A \sin{\left(\sqrt{\frac{D}{m}} \cdot t + \varphi \right)} = 8\text{cm} \sin{\left(\sqrt{\frac{D}{m}} \cdot 0 \text{s} + \varphi\right)})
So, jetzt hast Du die kompletten Bewegungsgleichungen fertig und mußt nur noch für t die Zeitpunkte einsetzen, die Dich "interessieren". Du bekommst jetzt für jeden Zeitpunkt eine Auslenkung (s(t)), eine Geschwindigkeit (v(t)) und eine Beschleunigung (a(t)) raus. Das ist doch schonmal eine tolle Sache, oder?
Gruß
Marco
|
|
|
para
Moderator
Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
| para Verfasst am: 18. Feb 2006 13:47 Titel: Re: Federpendel |
|
|
Okay, gehen wir das ganze am besten mal schrittweise an ...
| Code: | | Ein federpendel der masse m=600g wird aus seiner gleichgewichtslage um 8cm angehoben und dann losgelassen. Beim loslassen liegt der zeitnullpunkt. Die federkonstante beträgt D=1,20N/cm. |
| stk hat Folgendes geschrieben: | | Was ist die gleichgewichtslage ? Es ist doch der punkt an dem das federpendel quasi stehen bleibt, gleichen sich da die kraft die nach unten wirkt und die kraft die vom federpendel ausgeht und nach oben wirkt aus ? |
Wie ein Federpendel aussieht weißt du, oder? Im wesentlichen handelt es sich dabei ja um eine Feder, an die ein Gewicht gehängt wird. Hängst du das Gewicht ruhig an (also ohne Schwingung), wird die Feder auf Grund der Gewichtskraft etwas gedehnt. In der Lage die das Gewicht dann einnimmt sind Gewichtskraft und Federspannkraft gleich groß. Diese Lage wird als Gleichgewichtslage bezeichnet und stellt immer den Mittelpunkt einer (harmonischen) Schwingung des Federschwingers dar. Die Aussage dass sich die Kräfte ausgleichen stimmt also. Allerdings bleibt das Gewicht bei einer Schwingung in dieser Lage nicht stehen, sondern hat dort sogar seine maximale Geschwindigkeit.
| stk hat Folgendes geschrieben: | | wenn das pendel um 8cm angehoben wird, ist das dann schon meine amplitude ? |
Ja, genau.
| stk hat Folgendes geschrieben: | | Zeitnullpunkt - was hat das für mich zu bedeuten? |
Das heißt nur, dass zu diesem Zeitpunkt die Zeitmessung gestartet wurde. Das heißt dass im Moment des Loslassens die Stoppuhr bei t=0s gedrückt wurde und von da an die Zeit zählt. Der Nullpunkt der Zeitmessung ist für die erste Teilaufgabe entscheidend.
| Code: | | a) berechnen sie die auslenkung zum zeitpunkt t=0,15s |
Kennst du die allgemeine Formel für die Auslenkung bei einem harmonischen Federschwinger?
 = \hat{x} \cdot \cos( \omega \cdot t + \varphi)) oder  = \hat{x} \cdot \sin( \omega \cdot t + \varphi))
Wobei das x-Dach die Amplitude, das Omega die Kreisfrequenz und das Phi die Phase ist. Die Amplitude hast du schon. Das Phi trifft jetzt eine Aussage darüber, wo sich das Pendel zum Zeitpunkt t=0 befindet. Dabei unterscheiden sich natürlich die Sinus- und die Cosinusform der Gleichung. Wie man sich anhand des Verlaufs der Winkelfunktionen verdeutlichen kann gilt z.B. für die Cosinusform für t=0:
 = \hat{x} \rightarrow \text{maximale positive Auslenkung zu Beginn der Zeitmessung})
 = 0 \rightarrow \text{Durchgang durch die GG-Lage auf dem Weg zur negativen Auslenkung zu Beginn der Zeitmessung})
 = -\hat{x} \rightarrow \text{maximale negative Auslenkung zu Beginn der Zeitmessung})
 = 0 \rightarrow \text{Durchgang durch die GG-Lage auf dem Weg zur positiven Auslenkung zu Beginn der Zeitmessung})
Was wäre also in diesem Fall dein Phi?
Für die Kreisfrequenz solltest man die Formel kennen, sonst kommt man nicht weit. Der Zusammenhang zwischen Kreisfrequenz, Masse und Federkonstante ist:
Wie sieht also jetzt deine Schwingungsgleichung insgesamt aus? Wenn du dort t=0,15s einsetzt kommst du auf deine Auslenkung die gefragt ist. Auf was kommst du da?
| Code: | | b) berechnen sie die maximale geschwindigkeit des federpendels |
Wie ich oben schonmal gesagt hatte: bei einer harmonischen Schwingung ist die Geschwindigkeit immer beim Durchlauf durch die GG-Lage maximal. Am einfachsten gehst du dabei wohl mit dem Energieerhaltungssatz ran. Beim Federschwinger wird ja beständig Federspannenergie in kinetische Energie umgewandelt und umgekehrt. An den Umkehrpunkten (maximale positive und negative Auslenkung) steckt die gesamte Energie in der Feder, in der Gleichgewichtslage liegt die Gesamtenergie als kinetische Energie vor. Du berechnest also am besten die Energie die du in die Schwingung reingesteckt hast, als du den Körper um 8cm aus seiner GG-Lage ausgelenkt hat. Wird diese in kinetische Energie umgewandelt, kannst du auf die Geschwindigkeit des Pendelkörpers schließen. Die Formeln für kinetische Energie und Federspannenergie kennst du, oder?
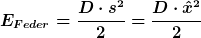
Was erhältst du also für die kinetische Energie?
Versuch' mal meinen Erläuterungen zu folgen, frag' wenn was unklar ist und poste anschließend mal deine Ergebnisse (bzw. die Zwischenergebnisse auf meine Fragen). Man lernt immer noch am besten, wenn man es selbst machen muss.
//edit: hm, jetzt war der marco schneller, naja ... doppelt hält besser, poste trotzdem mal deine Ergebnisse.
_________________
Formeln mit LaTeX
Zuletzt bearbeitet von para am 18. Feb 2006 14:03, insgesamt einmal bearbeitet |
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
| as_string Verfasst am: 18. Feb 2006 13:54 Titel: |
|
|
LOL!
In der Zwischenzeit hatte sogar Toxman schon gepostet (wenn ich das richtig gesehen habe), dann aber gleich wieder zurück gezogen. Schade eigentlich! Ich finde es immer gut, wenn es mehrere ähnliche Antworten gibt, weil die das ganze ja immer auch aus unterschiedlichen Blickwinkeln und auf unterschiedliche Art darstellen! Und die von Toxman hatte nochmal ein paar andere Punkte genannt, die nicht schlecht waren, finde ich.
Mir passiert es auch ständig, dass ich beim Abschicken eines Posts feststelle, dass fast genau das selbe schon jemand vorher geschrieben hat. Diesmal war ich sogar erster!  sonst ist das eher die Ausnahme.
Gruß
Marco
|
|
|
stk
Gast
|
| stk Verfasst am: 18. Feb 2006 14:07 Titel: |
|
|
ihr jungs seid klasse !
Danke für die antworten und die ausführungen ! Das hilft mir echt weiter, eine solche detailreiche erklärung fehlt mir im unterricht meistens, bzw ich kann sowas besser nachlesen als direkt vom lehrer aufgreifen. Im buch sind die erklärungen eher bescheiden.
Ich werde das ganze nochmal neu rechnen und dann später meine lösungen hier reinschreiben.
In der klausur gehts auch noch um fadenpendel und differentialgleichung, ich werd fragen dazu dann auch hier reinposten, dann habe ich nicht 3 unterschiedliche threads
gruß
stk
|
|
|
stk
Gast
|
| stk Verfasst am: 18. Feb 2006 18:26 Titel: |
|
|
ich habe es nun nach as_strings anleitung angefangen.
Ich komme jedoch nicht auf 1=sinPhi
bei mir steht da:
s(0) = 8cm * sin (14,14*1/s *0s +Phi)
wie soll ich denn dann auf 1 = sinPhi kommen ?
|
|
|
stk
Gast
|
| stk Verfasst am: 18. Feb 2006 18:32 Titel: |
|
|
sorry, als gast kann ich meinen beitrag nicht editieren 
nach paras beschreibung würde ich für phi natürlich = 0 wählen, weil meine 8cm ja die maximale positive auslenkung sind !
und bei meiner "rechnung" würde doch auch 0 = sinPhi rauskommen, oder ?
|
|
|
Nikolas
Ehrenmitglied
Anmeldungsdatum: 14.03.2004
Beiträge: 1873
Wohnort: Freiburg im Brsg.
|
| Nikolas Verfasst am: 18. Feb 2006 18:58 Titel: |
|
|
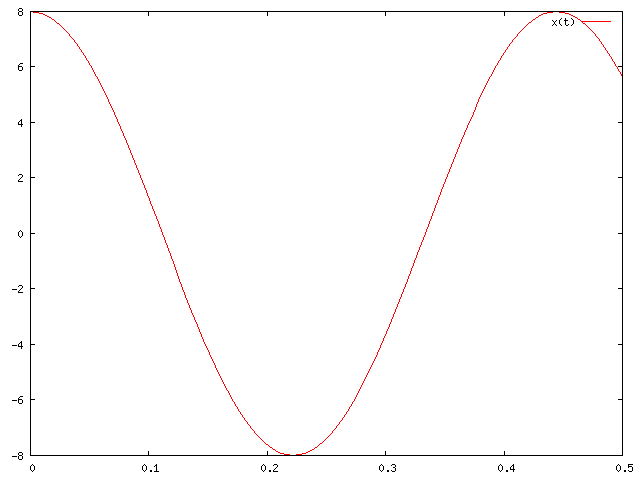
Das phi kann man bei diesen ANfangsbedingungen einfach auf 0 setzen, wenn du als Gleichung x(t)=x_max*cos(wt) wählst.
Zur Maximalgeschwindigkeit: Man braucht hier den EES nicht unbedingt:
wenn gilt: =x*cos(\omega t) \ gilt \ x'(t)=v(t)=-\omega * x* sin( \omega t)) Also schwankt die Geschwindigkeit zwischen 
Da du omega schon ausgerechnet hast und x gegeben, kommst du so schneller an die maximale Geschwindigkeit.
_________________
Nikolas, the mod formerly known as Toxman.
Erwarte das Beste und sei auf das Schlimmste vorbereitet. |
|
|
stk
Gast
|
| stk Verfasst am: 18. Feb 2006 23:24 Titel: |
|
|
| Toxman hat Folgendes geschrieben: | Das phi kann man bei diesen ANfangsbedingungen einfach auf 0 setzen, wenn du als Gleichung x(t)=x_max*cos(wt) wählst.
Zur Maximalgeschwindigkeit: Man braucht hier den EES nicht unbedingt:
wenn gilt: Also schwankt die Geschwindigkeit zwischen
Da du omega schon ausgerechnet hast und x gegeben, kommst du so schneller an die maximale Geschwindigkeit. |
hab ich denn jetzt irgendwas falsch gemacht in meiner gleichung, oder wie ?
|
|
|
stk
Gast
|
| stk Verfasst am: 19. Feb 2006 00:16 Titel: |
|
|
ist folgende annahme richtig:
Wenn wir das federpendel um 8cm anheben haben wir somit das maximum im positen bereich, das ist ja klar.
Wenn man sich das ganze auf einem einheitskreis vorstellt, bedeutet dass dann, dass wir bei 0° stehen ? Bei 90° kommen wir in die gleichgewichtslage, bei 180° haben wir das negative maximum und bei 360° bzw 0° eben wieder das positive maximum. Kann ich mir das so vorstellen ?
|
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 19. Feb 2006 00:34 Titel: |
|
|
| stk hat Folgendes geschrieben: | ist folgende annahme richtig:
Wenn wir das federpendel um 8cm anheben haben wir somit das maximum im positen bereich, das ist ja klar.
Wenn man sich das ganze auf einem einheitskreis vorstellt, bedeutet dass dann, dass wir bei 0° stehen ? Bei 90° kommen wir in die gleichgewichtslage, bei 180° haben wir das negative maximum und bei 360° bzw 0° eben wieder das positive maximum. Kann ich mir das so vorstellen ? |
Ja, das stimmt.
Allerdings nur wenn du einen cos betrachtest. Der ist ja bei 0° maximal, also gleich 1.
Wenn du einen sin betrachtest, wie as_string das in seinen Formeln macht, dann ist der Sinus natürlich maximal (nämlich gleich 1) für 90°. 1 ist also der Wert des Sinus für den Anfangszeitpunkt t=0. Mit dieser Überlegung kommt man auf sin(phi) = 1 und phi = 90° .
|
|
|
Nikolas
Ehrenmitglied
Anmeldungsdatum: 14.03.2004
Beiträge: 1873
Wohnort: Freiburg im Brsg.
|
| Nikolas Verfasst am: 19. Feb 2006 10:10 Titel: |
|
|
| stk hat Folgendes geschrieben: | | hab ich denn jetzt irgendwas falsch gemacht in meiner gleichung, oder wie ? |
Nein. Man geht hier ja von der DGL  aus.
Sowohl x=cos(wt+phi) als auch x= sin(wt+phi) löst diese Gleichung. Welchen Ansatz man jetzt wählt ist einem bei einem Start aus der Ruhe egal. Ich hab einfach den gewählt, bei dem ich mich um das Phi nicht kümmern muss.
_________________
Nikolas, the mod formerly known as Toxman.
Erwarte das Beste und sei auf das Schlimmste vorbereitet. |
|
|
Gast
|
| Gast Verfasst am: 19. Feb 2006 11:43 Titel: stk |
|
|
hi
für s(0,15) habe ich 6,819cm raus.
Für die maximale geschwindigkeit bin ich mit paras weg nicht auf ne gescheite lösung gekommen, ich denke es liegt daran, dass ich falsch umgeformt habe.
habe dann die v(t) formel genommen, das t habe ich einfach ausser acht gelassen.
Meine lösung war dann gerundet 8cm/s.
|
|
|
stk
Gast
|
| stk Verfasst am: 19. Feb 2006 12:05 Titel: |
|
|
eine weitere aufgabe ausm buch
Der Körper eines federpendels hat die masse m=200g, er schwingt mit T=1,25s und der amplitude s = 5,0cm. Mit welcher geschwindigkeit geht er durch die gleichgewichtslage ?
habe dann halt über T=2pi/w mein w gekriegt, dann über w=wurzel von d/m mein D (5,021kg/s²) und dann in den energieerhaltungssatz eingesetzt.
Habe 25,12cm/s raus. Kann das?
|
|
|
stk
Gast
|
| stk Verfasst am: 19. Feb 2006 12:44 Titel: |
|
|
ich sollte mich langsam echt mal anmelden...
Ich hoffe mal meine Federpendel berechnungen waren soweit richtig. Zum Fadenpendel habe ich keine fragen, hab damit gott sei dank keine solchen probleme 
Allerdings gibt es aber eine weitere nuss, die es zu knacken gilt.Erstmal die herleitung der differentialfunktion und weiterhin die herleitung der lösungsfunktion eines harmonischen oszillators... Ich weiss echt nicht, wie ich das verstehen soll. Man nimmt verschiedene formeln und wurschtelt die alle zusammen, aber irgendwie steig ich da nicht dahinter.
|
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
| as_string Verfasst am: 19. Feb 2006 14:00 Titel: |
|
|
Hallo!
Zum Fadenpendel:
Erstmal ja... Dein Ergebnis stimmt! Ich bin mir aber nicht so sicher, ob Dein Physiklehrer das mit D ausrechnen beim Fadenpendel so gut findet, wenn es auch nicht wirklich falsch ist... Eigentlich gibt es kein richtiges D bei einem Fadenpendel. Immerhin ist D ja die "Federkonstante". Allerdings hat man in der "kleine Winkel Näherung" auch sowas wie eine Federhärte, weshalb das eigentlich schon einigermaßen richtig ist.
Aber insgesamt finde ich den Weg bei dieser Aufgabe über die Energieerhaltung etwas ungeschickt. Wenn Du Dir nochmal meine drei Bewegungsgleichungen anschaust, dann stellst Du vielleicht fest, dass sowohl der Sinus als auch der cos immer maximal =1 werden können, einmal bei 90° beim Sinus und bei 0° beim Kosinus. Wenn Du jetzt nach der Maximalen Auslenkung (Amplitude) oder Geschwindigkeit oder Beschleunigung gefragt wirst, kannst Du dieses Wissen einsetzen und bekommst für die Werte (wie in diesem Thread auch schon geschrieben wurde...):
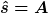
Ich habe also das mit sin/cos was ursprünglich noch hintendran kam einfach auf 1 gesetzt und schon kam ich auf die Maximalwerte.
Wir müssen bei der Aufgabe also einfach nur  ausrechnen, wobei A schon gegeben ist und von T ausgerechnet werden kann, wie Du das ja schon getan hast:
Gruß
Marco
|
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
| as_string Verfasst am: 19. Feb 2006 14:56 Titel: |
|
|
Hallo!
Ich bekomme übrigens für die maximale Geschwindigkeit beim Federpendel 1,13 m/s raus. Wahrscheinlich hast Du wirklich das Omega falsch, oder?
Gruß
Marco
|
|
|
stk
Gast
|
| stk Verfasst am: 19. Feb 2006 15:09 Titel: |
|
|
nein, für omega hatte ich auch 14,14 raus. Komisch...
mein letzter schritt war
s(0,15)=8cm*sin(14,14*0,15)
dann hab ich halt 8cm*sin(2,121) sind 6,819.
Komisch.
für die geschwindigkeit hatte ich folgendes:
(120kg*m*64cm²)/(2*m*s²).
da hab ich dann 51200cm²/s² = v² raus.
|
|
|
stk
Gast
|
| stk Verfasst am: 19. Feb 2006 15:19 Titel: |
|
|
hier nun eine etwas schwierigere aufgabe:
hängt man einen körper der masse 400g an eine schraubenfeder, so wird sie um 10cm verlängert. Aus dieser gleichgewichtslage hebt man den körper um 5cm an und lässt ihn los.
a) mit welcher frequenz schwingt dieses federpendel?
b) wie viel schwingungsenergie enthält es?
wie würde man da rangehen, wenn man auch noch wissen wollte zu welcher zeit und mit welcher geschwindigkeit die gleichgewichtslage "durchfahren" werden würde ?
|
|
|
Nikolas
Ehrenmitglied
Anmeldungsdatum: 14.03.2004
Beiträge: 1873
Wohnort: Freiburg im Brsg.
|
| Nikolas Verfasst am: 19. Feb 2006 15:25 Titel: |
|
|
| Zitat: | | a) mit welcher frequenz schwingt dieses federpendel? |
Aus der Masse und der Verlängerung kannst du die Federkonstante ausrechnen und aus der Zusammen mit der Masse, das omega.
Mit omega=2 pi f, hast du dann die Frequenz.
| Zitat: | | wie würde man da rangehen, wenn man auch noch wissen wollte zu welcher zeit und mit welcher geschwindigkeit die gleichgewichtslage "durchfahren" werden würde ? |
Überleg mal, wie sich das Pendel während einer Periode bewegt.
Bei t=0 ist es ganz oben, bei t=T/2 ganz unten. Wann ist es dementsprechend in der Mitte?
| Zitat: | | mit welcher geschwindigkeit |
Die Frage wurde schon ein paar mal in diesem Thread exakt beantwortet.
_________________
Nikolas, the mod formerly known as Toxman.
Erwarte das Beste und sei auf das Schlimmste vorbereitet. |
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
| as_string Verfasst am: 19. Feb 2006 15:47 Titel: Differentialgleichung eines harmonischen Oszillators |
|
|
Hallo!
So, jetzt kommt die "weitere Nuss"!
Differentialgleichung eines harmonischen Oszillators
Ein harmonischer Oszillator zeichnet sich dadurch aus, dass es ein harmonisches Potential gibt, in dem sich ein Körper mit einer Masse bewegt. Das harmonische Potential führt zu einer rücktreibenden Kraft, die bei einer Auslenkung des Oszillators um die Strecke  auf den Körper entgegen der Auslenkungsrichtung wirkt und betragsmäßig proportional zu der Auslenkung ist:
Da aus der Kraft eine Beschleunigung resultiert kann man weiter schreiben:
Wir wollen das jetzt mal nur eindimensional betrachten, was hier ja auch Sinn macht, weil die Bewegung sich nur auf einer Dimension abspielen wird. Selbst beim Fadenpendel kann man eine "generalisierte Koordinate" einführen, die einfach nur die Postition des Körpers auf der durch den Faden aufgezwungenen Kreisbahn beschreibt. Oder anders ausgedrückt: Es genügt auch beim Fadenpendel nur einen Wert an zu geben, um die Auslenkung fest zu legen, obwohl sich der Körper natürlich schon in mehreren Dimensionen bewegen kann.
Also kann man die Gleichung eindimensional auch so schreiben:
Jetzt kommt aber der große Trick, der diese Gleichung gleich zu einer Differentialgleichung macht: Die Ableitung einer Position (Strecke, Ort x oder wie man das sonst noch nennt...) nach der Zeit ist eine Geschwindigkeit und die Ableitung einer Geschwindigkeit nach der Zeit ist eine Beschleunigung. Den Punkt mußt Du verstehen! Darauf basiert so vieles! Wenn Du nicht weißt, was das bedeutet, dann frag' nochmal nach!
Ableitungen nach der Zeit macht man ja gerne mit Pünktchen auf den Größen, so wie man Ableitungen nach dem Ort mit dem Strich dran macht. Deshalb schreibt man dann:
Wenn man das noch auf eine Seite bringt, dann hat man schon die Differenzialgleichung in der bekannt Form (manche multiplizieren das ganze auch nochmal mit m, um nicht die Beschleunigungen, sondern die Kräfte dastehen zu haben, aber das ist jetzt mal wurscht!)
Diese DGL muß jetzt also gelöst werden. Eigentlich haben wir die Lösung schon die ganze Zeit verwendet, aber naja...
Wenn man sich die Gleichung anschaut, stellt man sofort fest: Das ist ja eine lineare Differentialgleichung 2. Grades! 
Eigentlich mußt Du nicht wirklich wissen, wie man solche DGLs lösen kann. In Wirklichkeit ist das auch eine Wissenschaft für sich. Es gibt nur wenige Spezialfälle, wo man wirklich Methoden hat, mit denen man so was systematisch lösen kann. Es gibt aber auch unheimlich viele Methoden zur Lösung von DGLs, bei denen man oft nicht weiß, welche man denn jetzt wirklich zum Ziel führt. Die allermeisten Probleme in der Physik führen auf jeden Fall auf irgendeine Art von DGL und deshalb ist es eigentlich für einen Physiker besonders wichtig, solche Dinger lösen zu können.
Lineare DGLs sind aber besonders leicht! Man hat da mal einen Lösungsansatz gefunden, der die alle löst und man muß nur noch einsetzen um ein paar Konstanten zu bestimmen... fertig. Normalerweise macht man allerdings diesen Ansatz mit komplexen Zahlen:
 = A e^{Bt+C})
wobei zumindest B auch komplex sein kann und damit die ganze Funktion. Das will ich DIr jetzt hier nicht zumuten, weshalb ich den einfacheren sin/cos Ansatz nehme. Das ist in diesem Fall dann zwar schon fast die Lösung, aber naja... Der Trick dabei ist, dass man ja weiß, dass, wenn man Sinus oder Kosinus zweimal ableitet, schon wieder ein Sinus/Kosinus rauskommt. Wenn Du Dir die Gleichung anschaust, siehst Du vielleicht, dass das von Vorteil sein könnte, weil sich mit etwas Geschick die beiden Summanden dann wirklich wegheben könnten und das ganze zu 0 werden könnte. Also machen wir einfach mal "auf gut Glück" einen Ansatz:
 = A\cdot \sin{\left(\omega t + \varphi\right)})
Wahrscheinlich kommt Dir das bekannt vor... Aber ich kann's leider nicht ändern! Es ist wirklich so eine "ratemal Sache"...
Aber was wir an dieser Stelle noch nicht wissen ist Omega! Das müssen wir schon noch ausrechnen. Dafür mache ich zweimal die Ableitung nach der Zeit und setze in die ursprüngliche DGL ein. Das Einsetzen muß man so wie so noch machen, weil man ja sehen will, ob unser Ansatz denn überhaupt auch die DGL erfüllt. Übrigens: Der Ansatz funktioniert genau so auch mit Kosinus statt Sinus.
Also hier die Ableitungen:
 = A \omega \cdot \cos{\left(\omega t + \varphi\right)})
 = -A \omega^2 \cdot \sin{\left(\omega t + \varphi\right)})
Du siehst also: Aus der inneren Funktion kommt immer ein Omega raus, so dass in der zweiten Ableitung dann ein Omega zum Quadrat da ist. Das sin wird nach einmal ableiten zum cos und dann zum -sin. Das ist schon alles, also etwas Kettenregel und wissen, wie man sin/cos ableitet... fertig!
Das setzen wir jetzt in unsere ursprüngliche DGL ein:
} + \frac{D}{m}\cdot A\cdot \sin{\left(\omega t + \varphi\right)} = 0)
Wenn man das jetzt durch den Sinus teilt und auch durch A dann steht das hier schon da:
Was hat uns das ganze also jetzt gebracht? Erstens hab ich mit dem Einsetzen bewiesen, dass unser Ansatz die DGL löst. Das ist schonmal sehr wichtig! Sonst bräuchten wir ja nicht weiter rechnen. Zweitens konnte ich eine Konstante vom Ansatz, nämlich schon mal bestimmen. Das ist sehr wichtig, um überhaupt etwas berechnen zu können.
Allerdings blieben zwei Konstanten unbestimmt, nämlich die Amplitude A und der Phasenwinkel . Das ist aber auch gut so! Bei solchen DGL ist nämlich auch immer wichtig: Es gibt Anfangsbedingungen, die irgendwie in der Aufgabe drin stehen müssen. Bei uns war z. B. für t=0 das hier gegeben: v0 = 0 und x0 = 8cm. Das sind zwei Angaben, mit denen ich die zwei Konstanten bestimmen kann und schon habe ich meine fertigen Bewegungsgleichungen!
Übrigens ist es gut, dass zwei freie Konstanten noch drin stehen. Das muß bei einer DGL 2. Ordnung nämlich immer so sein! Sonst wäre unser Ansatz zwar immer noch richtig, aber nicht vollständig gewesen. Wir hätten dann nur eine spezielle Lösung und keine allgemeine gefunden. So ist aber alles wunderbar!
Gruß
Marco
|
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
| as_string Verfasst am: 19. Feb 2006 18:31 Titel: |
|
|
| stk hat Folgendes geschrieben: | nein, für omega hatte ich auch 14,14 raus. Komisch...
mein letzter schritt war
s(0,15)=8cm*sin(14,14*0,15)
dann hab ich halt 8cm*sin(2,121) sind 6,819. |
OK. Da haben wir das Problem! Das war dann wohl doch noch nicht ganz klar mit dem Phasenwinkel.
Ich versuche mal das nochmal zusammen zu fassen, obwohl schon alles in diesem Thread dazu gesagt wurde:
Du hast als Lösung für die DGL diese Funktion:
 = A \sin{\left(\omega t + \varphi\right)})
Wenn man will, kann man auch mit Kosinus arbeiten und bekommt dann ebenso die Lösung:
 = A \cos{\left(\omega t + \varphi\right)})
ABER VORSICHT!!! Das Phi von der ersten Gleichung ist jetzt ein anderes als von der zweiten! Das nicht durcheinander bringen!
Die beiden Parameter A und Phi mußt Du jetzt aus den Anfangsbedingungen bestimmen. Die schreib ich hier nochmal etwas abgewandelt hin:
 = 8\text{cm})
und als Geschwindigkeit hast Du am Anfang 0:
 = 0\frac{\text{m}}{\text{s}})
Ich nehme jetzt mal wieder meinen Ansatz mit Sinus, aber mit Kosinus funktioniert das genau so gut. Nur eben, dass Phi anders ist.
 = A \sin{\left(\omega t + \varphi\right)} = 8\text{cm})
Ich habe also nur t = 0 gesetzt. So jetzt aber die Geschwindigkeit:
 = A\omega \cos{\varphi} = 0\frac{\text{m}}{\text{s}})
Wenn ich davon ausgehe, dass weder A noch Omega null ist, muss der cos null sein. Wann ist der Kosinus aber = 0? Genau! Bei:
 und bei:
Man könnte jetzt mit beiden Winkeln weiter rechnen, aber da mir es so besser gefällt, nehme ich den pi/2 (das sind 90°) Winkel. Das setze ich wieder in die erste Gleichung, also die mit x(0) ein und bekommen:
Da der Sinus von Pi/2 aber =1 ist, bekomme ich die Gleichung:
Damit habe ich meine beiden freien Konstanten bestimmt und ich kann die Bewegungsgleichungen aufstellen. Und da ist Dein Fehler: Wenn Du Sinus nimmst, dann mußt Du auch immer noch den Phi = Pi/2 addieren, bevor Du auf dem Taschenrechner die Sinus-Taste drückst! Wenn Du von Anfang an mit Kosinus los gegangen wärst, dann würdest Du 0 für Phi rausbekommen und könntest den dann ganz weg lassen. Das liegt aber nur an der Aufgabenstellung, bzw. wann bei der Aufgabe die Zeit t = 0 ist. Dadurch würde die Rechnung aber etwas einfach werden, das ist schon alles.
Gruß
Marco
Zuletzt bearbeitet von as_string am 18. Dez 2006 03:45, insgesamt einmal bearbeitet |
|
|
nepton
Anmeldungsdatum: 02.12.2006
Beiträge: 24
|
| nepton Verfasst am: 03. Dez 2006 14:57 Titel: |
|
|
Hallo,
ich habe eine ähnliche Aufgabe, die ich nicht alleine rechnen kann :
Ein horizontales, ungedämpftes Federpendel (Masse=0,15 kg) wird zur zeit t=0 um 5 cm ausgelenkt und wird dann losgelassen . Für die Auslenkung von 5 cm muß eine Spannarbeit von 0,25 J geleistet werden. Berechnen Sie
a) die maximale Geschwindigkeit des Pendels
b)die Auslenkung zur Zeit t1= 0,05 s
c) die kinetische Energie zur Zeit t2= 0,05
d) nun sei das Pendel gedämpft und die Amplitude nimmt vn einem Maximum zum nächsten um 10% ab. wie groß ist die Reibungskraft bei v= 1 m/s?
also ich habe zu a)
gerechnet :
w= wurzel aus (D/m)
v(t) = A w cos (w*t + phi)
A =0,05m
s= 0,05m ???
dafür solte man als erstes D rechnen dan w
Arbeit = F *s -->F= 0,25J / 0,05m = 5 N
D = F/S oder
D =mg /s ????
ich komme nicht weiter  , bitte helfen welchen wert soll ich für phi, s einsetzen???
Danke im vorraus
gruß nepton
|
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
| as_string Verfasst am: 04. Dez 2006 21:15 Titel: |
|
|
Hallo!
| nepton hat Folgendes geschrieben: |
also ich habe zu a)
gerechnet :
w= wurzel aus (D/m)
v(t) = A w cos (w*t + phi)
A =0,05m
s= 0,05m ???
|
Das sieht doch schon ganz gut aus! nur das mit dem s=... gefällt mir noch nicht so gut. s ist ja normalerweise die Auslenkung und die hängt auch von der Zeit ab, also:
 = A\cdot \sin(\omega t+\varphi))
Die Gleichung brauchst Du noch später, ich komme darauf nochmal zurück.
| nepton hat Folgendes geschrieben: | | Arbeit = F *s -->F= 0,25J / 0,05m = 5 N |
Diese Gleichung ist nur richtig, wenn die Kraft F über die gesamte Strecke s konstant ist (genauer, wenn das Skalarprodukt aus F und jedem kleinen Wegstückchen ds über den ganzen Weg konstant ist). Das ist hier leider nicht der Fall, weil die Kraft ja immer größer wird, je weiter die Feder(n) ausgelenkt wird (werden). Für die Arbeit bei der Feder (vielleicht auch Spannarbeit/-energie) habt Ihr wahrscheinlich eine eigene Formel gelernt, oder?
| nepton hat Folgendes geschrieben: |
D = F/S oder
D =mg /s ????
|
Eigentlich ist die zweite Formel ein Spezialfall der ersten, aber nur für ein senkrechtes Federpendel. Bei dem ungedämpften kannst Du einfach die erste nehmen und die beiden Werte für Auslenkung und Kraft einsetzen, die in der Aufgabe angegeben sind.
| nepton hat Folgendes geschrieben: | | ich komme nicht weiter , bitte helfen welchen wert soll ich für phi, s einsetzen??? |
Ja, jetzt zu :
Du hast die Formel für s(t) von oben. Wenn Du jetzt die Anfangsbedingungen direkt einsetzt, steht das hier da:
 = 0{,}05\text{m} = A\cdot\sin(\phi))
und für die Geschwindigkeit (soll ja am Anfang keine haben, weil es festgehalten wird):
 = 0 = A\omega\cdot \cos(\phi))
die Gleichung aus der Geschwindigkeit sagt Dir schon was über aus. Mal angenommen, dass weder A noch 0 sind, dann muss der Kosinus 0 sein. Und das ist er z. B. bei , aber auch bei 270°. Wenn man die Gleichung aus s(t) anschaut, dann sieht man aber, dass der Sinus besser positiv sein sollte und so bietet sich 90° eher an (obwohl es auch mit 270° ginge, aber ich will Dich nicht unnötig verwirren...).
Also haben wir den Phasenwinkel schon mal zu 90° bestimmt und können den auch dann in die erste Gleichung einsetzen:
 = 0{,}05\text{m} = A\cdot\sin(90°) = A)
Weil der Sinus von 90° gerade +1 ist, haben wir so direkt schon die Amplitude A bestimmt, und zwar zu 5cm.
Damit sind alle Konstanten bestimmt (Omega noch aus den Angaben) und Du hast eine Gleichung für die Auslenkung s und die Geschwindigkeit v zu jedem Zeitpunkt:
 = 0{,}05\text{m}\cdot \sin(\omega t+90°))
 = 0{,}05\text{m}\omega\cdot \cos(\omega t+90°))
Wobei Du aber natürlich erstmal A und in den Formeln drin stehen lassen solltest, damit es mit den Zahlen nachher nicht unübersichlicher wird, als es unbedingt sein muss. Damit kannst Du jetzt die Auslenkung und die Geschwindigkeit zu jedem beliebigen Zeitpunkt ausrechnen. Die kin. Energie kannst Du aus der Geschwindigkeit ausrechnen.
Soweit erstmal...
Gruß
Marco
|
|
|
nepton
Anmeldungsdatum: 02.12.2006
Beiträge: 24
|
| nepton Verfasst am: 07. Dez 2006 21:40 Titel: |
|
|
Hallo,
danke für die Erklärung
zu d) weiss ich nicht in welchen Formel eisetzen soll!!
(die mit der Reibungskraft)
Gruß
nepton
|
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 07. Dez 2006 22:15 Titel: |
|
|
Ich denke, die Formel für d) sollst du dir selbst herleiten (Außer du findest etwas in deinen Aufschrieben, was genau dazu passt).
Ich würde hier annehmen, dass die Reibungskraft proportional zur Geschwindigkeit v(t) ist,
und die verlorengegangene Energie mit einem Integral berechnen, das du aus "Reibungskraft (t) * Weg (t)" für eine Schwingungsperiode aufstellen kannst.
|
|
|
nepton
Anmeldungsdatum: 02.12.2006
Beiträge: 24
|
| nepton Verfasst am: 08. Dez 2006 12:31 Titel: |
|
|
Hi,
Reibungskraft F= -b*v kann man mit dieser formel rechnen?????????
ich suche eine einfachen Weg!!
könne Sie mir weiter erklären .
Gruß
nepton
|
|
|
nepton
Anmeldungsdatum: 02.12.2006
Beiträge: 24
|
| nepton Verfasst am: 10. Dez 2006 13:57 Titel: |
|
|
Hallo,
würden Sie mir bitte weiter helfen zu d)
Danke im voraus
Gruß
nepton
|
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 11. Dez 2006 01:19 Titel: |
|
|
| nepton hat Folgendes geschrieben: |
Reibungskraft F= -b*v kann man mit dieser formel rechnen?????????
|
So eine Formel kannst du verwenden, um dir eine Formel für die d) so herzuleiten, wie ich es oben angedeutet habe.
| Zitat: |
ich suche eine einfachen Weg!!
|
Der einfachste Weg könnte sein, wenn du es schaffst, in deinen Aufschrieben oder in den Quellen, die du zum Lösen der Aufgabe zur Verfügung hast, nachzuschlagen und Formeln zu finden, mit denen du so etwas berechnen kannst.
------------------------
Ich kann ehrlich gesagt noch nicht erraten, was du in dieser Aufgabe lernen und üben sollst. Ist das eine Schulaufgabe oder eine Uniaufgabe, und was habt ihr zu dem Thema bisher schon an Formeln hergeleitet und/ oder gelernt?
Ich kann bisher schwer einschätzen, auf was für einen Lösungsweg ich dich führen könnte, weil ich nicht weiß, welche fertigen Formeln oder welche Rechenmethoden du bereits kennst und kannst (oder kennen und können oder üben sollst).
Eine fertige Formel, die die Aufgabe d) löst, kenne ich nicht auswendig. Was hast du dir selbst schon dazu überlegt, und hast du schon etwas in deinen Aufschrieben gefunden, von dem du glaubst, dass es hier einen Ansatzpunkt darstellen könnte, der dir weiterhelfen kann?
|
|
|
nepton
Anmeldungsdatum: 02.12.2006
Beiträge: 24
|
| nepton Verfasst am: 12. Dez 2006 12:43 Titel: |
|
|
Hallo,
also ich studiere Chemie und das ist eine Übungsaufgabe für die Prüfung Experimentalphysik .
zu d) habe viel nachgedach aber die formel kann ich icht herleiten!!
das Endergebnis soll 0,1836 kg/s sein ,aber was ich nicht verstehe ist die Einheit, denn hier auf dem Übungsaugaben steht das Endergebnis mit der Einheit kg/ s und nich N???
können Sie vielleicht mir helfen???
Danke im voraus
Gruß
nepton
|
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 12. Dez 2006 12:58 Titel: |
|
|
Die Einheit des Ergebnis, das man dir angegeben hat, ist die Einheit der Größe "Kraft pro Geschwindigkeit".
Das siehst du, wenn du berücksichtigst, dass 1 N = 1 kg * m / s^2 ist.
-------------------------------
Da das eine Uni-Aufgabe ist, halte ich es für wahrscheinlich, dass ihr euch die nötige Formel selbst herleiten sollt.
Dein Ansatz für die Reibungskraft  ist gut. Den kannst du nun verwenden, um die Energie zu berechnen, die während einder Schwingung verloren geht.
Kannst du ein Integral aufstellen, mit dem du das berechnen kannst? Kannst du dabei verwenden, dass Reibungskraft * Wegstück = verlorengegengene Energie ?
Versuche das mal, und schreibe hier auf, wie das Integral aussieht, auf das du kommst.
|
|
|
nepton
Anmeldungsdatum: 02.12.2006
Beiträge: 24
|
| nepton Verfasst am: 12. Dez 2006 14:32 Titel: |
|
|
also, ich bin im 1. semester.
f *s = verlorene Energie
Spannarbeit =0,25J
kinetische Energie =0,234J
erstmal wie soll ich verlorene energie rechnen?
F(t) = Energie/s
F(t)=E. /s *t+F0
mehr weiss ich nicht!!!!
gruß
nepton
|
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 12. Dez 2006 16:22 Titel: |
|
|
Beim Aufstellen einer Formel für die verlorene Energie musst du berücksichtigen, dass sich die Kraft F(t) ändert. Darum musst du das ganze hier stückweise rechnen, also ein Integral verwenden.
 \dd s)
Für das F(t) kannst du die Abhängigkeit von der Geschwindigkeit v(t) einsetzen, die du von oben kennst.
Das Integral geht über den gesamten während einer Schwingungsperiode zurückgelegten Weg.
Um das  in ein  umzuwandeln, brauchst du die Zeitabhängigkeit von s(t).
Dann bekommst du ein Integral über die Zeit t, das du ausrechnen kannst.
-----------------------------------------
Kannst du schon mit Integralen rechnen? Ich vermute, die hier benötigten mathematischen Grundlagen dürften die Haupthürde sein, die du überwinden musst, damit dieser Aufgabenteil für dich mach- und lösbar wird.
|
|
|
nepton
Anmeldungsdatum: 02.12.2006
Beiträge: 24
|
| nepton Verfasst am: 13. Dez 2006 12:07 Titel: |
|
|
gibt es kein anderen weg
ich verstehe das nicht !!!!!!!!!!!
bitte erklären Sie mir weiter!
Gruß
nepton
|
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 13. Dez 2006 20:38 Titel: |
|
|
Entschuldige, wenn du das bisherige noch nicht verstanden hast, dann kann ich nicht weitererklären, sondern dann müssen wir uns mit dem bisherigen Anfang der Erklärung auseinandersetzen. Die einzige Chance, dass du das nachvollziehen kannst, was ich hier erzähle, ist, wenn du auch den Anfang schon verstehen kannst, oder konkreter sagst, was du schon weißt und wo du glaubst, dass es bei dir noch hakt.
Einfach nur immer weitererklären, bis ich dir die ganze Lösung erzählt habe, macht hier keinen Sinn. Denn ich kann die Aufgabe ja nicht für dich lösen, sondern es macht nur Sinn, wenn wir dir helfen können, diese Aufgabe selbst zu lösen.
----------------------------------------
Um dir etwas zu erklären, muss ich wissen oder zumindest raten können, was du schon weißt und kannst und an was ich anknüpfen kann, damit du selbst anfangen kannst, etwas zu rechnen.
Deshalb frage ich dich noch einmal: Weißt du schon, was ein Integral ist? Kannst du schon mit Integralen rechnen? Was weißt du schon über Integrale?
|
|
|
|
|
Registrieren
Login
FAQ
Suchen
