| Autor |
Nachricht |
wasoren
Gast
|
 wasoren Verfasst am: 25. Nov 2015 15:47 Titel: Volumenintegral Kugelkoordinaten Kartesisches KOOS wasoren Verfasst am: 25. Nov 2015 15:47 Titel: Volumenintegral Kugelkoordinaten Kartesisches KOOS |
 |
|
Meine Frage:
Hi,
man nehme Kugelkoordinaten an:

Dann ist die Umrechnung in die kart. Koord.:



Wie kommt man auf

?
Btw: Es ist dV das infinitesimal kleine Volumenteilchen.
Meine Ideen:
Wohlwissend es ist

(per Definition)
Mithilfe der Umrechnung kann man schreiben

Dann ist

Wenn ich das für alle (x,y,z) mache, erhalte ich einen Term
dV = dxdydz = sin²...cos²sin usw etc mit ^3) noch am Ende. noch am Ende.
Aber wie komme ich auf einen Ausdruck, der Form

?
Viele Grüße |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8583
|
|
 |
wasoren
Gast
|
 wasoren Verfasst am: 25. Nov 2015 16:26 Titel: wasoren Verfasst am: 25. Nov 2015 16:26 Titel: |
 |
|
Geht das auch ohne Funktionaldeterminante ?
Wäre über einen einfachen Lösungsansatz erfreut (wenig Vorwissen)?
Was ich weiß, ist dass der Ansatz
dx/dr nach dx umstellen wohl zielführend sein soll.
dV ist dann das Produkt von dx * dy * dz
was ich als = dphi d theta dr darstellen möchte
Um das zu erreichen - fällt mir gerade auf - müsste ich ja z. B.
dx = .... dr
dy = .... dtheta
dz = .... dphi
umformen (sodass halt genau einmal je dr, dtheta dphi vorkommt)
Aber wie komme ich dann auf das kurze r²sin(theta), denn da sind so viele Faktoren drin? |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8583
|
 jh8979 Verfasst am: 25. Nov 2015 16:27 Titel: jh8979 Verfasst am: 25. Nov 2015 16:27 Titel: |
 |
|
| wasoren hat Folgendes geschrieben: | | Geht das auch ohne Funktionaldeterminante ? |
Nein, da dort die Funktionaldeterminante eben auftritt.
Die Berechnung geht zB über das Spatprodukt (siehe zweiter Link oben).
Zuletzt bearbeitet von jh8979 am 25. Nov 2015 18:02, insgesamt einmal bearbeitet |
|
 |
hansguckindieluft

Anmeldungsdatum: 23.12.2014
Beiträge: 1212
|
|
 |
wasoren
Gast
|
 wasoren Verfasst am: 25. Nov 2015 17:01 Titel: wasoren Verfasst am: 25. Nov 2015 17:01 Titel: |
 |
|
Danke, hat ganz gut geholfen.
Die geometische Erklärung ist sehr gut.
Dennoch wäre ich über einen Ansatz über die folgenden Gleichungen dankbar.
x = r sin theta cos phi
y = r sin theta sin phi
z = r cos theta
dx/dr = sin theta cos phi
dx = sin theta cos phi * dr
dy/dr = sin theta sin phi
dy = sin theta sin phi * dr
dz/dr = cos theta
dz = cos theta * dr
dV = dx dy dz
= sin theta cos phi sin theta sin phi cos theta * (dr)^3
Aber es soll dr dphi dtheta stehen (jeweils eine Kugelkoordinate statt drei mal eine Kugelkoord wie hier r)
Das geht doch bestimmt? (auch ohne viel mehr Vorwissen, 1 Semester) |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 25. Nov 2015 20:20 Titel: index_razor Verfasst am: 25. Nov 2015 20:20 Titel: |
 |
|
| wasoren hat Folgendes geschrieben: | Geht das auch ohne Funktionaldeterminante ?
Wäre über einen einfachen Lösungsansatz erfreut (wenig Vorwissen)?
|
In diesem Spezialfall geht es schon. Natürlich steckt letztendlich doch die Funktionaldeterminante dahinter, aber es gibt eine recht anschauliche Abkürzung für die Rechnung.
Die Formel  gilt für alle orthonormalen Koordiantensysteme, also solche, deren Basisvektoren in jedem Punkt senkrecht aufeinander stehen und auf die Länge Eins normiert sind. Anschaulich gesprochen ist ja das Volumenelement das Produkt aus drei Längeneinheiten in senkrecht aufeinander stehende Richtungen. Die sphärischen Koordinaten sind schon orthogonal, aber nicht normiert. Zwei der Koordinaten messen ja auch Winkel und keine Länge. Du mußt also nur geeignete Normierungsfaktoren für die Koordinatendifferentiale finden, d.h. in diesem Fall einfach statt der infinitesimalen Winkelzuwächse die zugehörigen infinitesimalen Bogenlängen betrachten, sagen wir gilt für alle orthonormalen Koordiantensysteme, also solche, deren Basisvektoren in jedem Punkt senkrecht aufeinander stehen und auf die Länge Eins normiert sind. Anschaulich gesprochen ist ja das Volumenelement das Produkt aus drei Längeneinheiten in senkrecht aufeinander stehende Richtungen. Die sphärischen Koordinaten sind schon orthogonal, aber nicht normiert. Zwei der Koordinaten messen ja auch Winkel und keine Länge. Du mußt also nur geeignete Normierungsfaktoren für die Koordinatendifferentiale finden, d.h. in diesem Fall einfach statt der infinitesimalen Winkelzuwächse die zugehörigen infinitesimalen Bogenlängen betrachten, sagen wir  und und  . Dann ist einfach . Dann ist einfach  (denn (denn  mißt ja, wie gesagt bereits eine Länge.) Die Bogenlängen rauszufinden ist aber ganz einfach über die Formel mißt ja, wie gesagt bereits eine Länge.) Die Bogenlängen rauszufinden ist aber ganz einfach über die Formel  . . 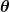 beschreibt einen Großkreis auf der Sphäre r=const., es gilt also beschreibt einen Großkreis auf der Sphäre r=const., es gilt also  . .  beschreibt einen Breitenkreis mit Radius beschreibt einen Breitenkreis mit Radius  . Das bedeutet . Das bedeutet  . Daraus ergibt sich sofort die gesuchte Formel . Daraus ergibt sich sofort die gesuchte Formel

| Zitat: |
Was ich weiß, ist dass der Ansatz
dx/dr nach dx umstellen wohl zielführend sein soll.
|
Du mußt eigentlich nichts umstellen. In deiner Überlegung steckt aber noch ein anderer Denkfehler: jede der kartesischen Koordinaten x,y,z hängt nicht nur von einer, sondern von mehreren sphärischen Koordinaten ab:

z.B. von  und und 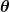 . Die Kordinatendifferentiale drücken lediglich diese Abhängigkeit in linearer Näherung aus. Es gilt also . Die Kordinatendifferentiale drücken lediglich diese Abhängigkeit in linearer Näherung aus. Es gilt also
 . (Bei dir fehlt der zweite Term.) Zusammen mit den entsprechenden Beziehungen für x und y ergibt dies ein lineares Gleichungssystem, dessen Koeffizientendeterminante die Volumenverzerrung bei der Transformation von kartesische in sphärische Koordinaten angibt und deren Wert eben gleich . (Bei dir fehlt der zweite Term.) Zusammen mit den entsprechenden Beziehungen für x und y ergibt dies ein lineares Gleichungssystem, dessen Koeffizientendeterminante die Volumenverzerrung bei der Transformation von kartesische in sphärische Koordinaten angibt und deren Wert eben gleich  ist. ist.
Man kann diese Determinante, bzw. das Volumenelement im Prinzip also als Produkt von drei Größen

\dd r + (...)\dd\phi + (...)\dd\theta,)
\dd r + (...)\dd\phi + (...)\dd\theta)
auffassen, so wie es dir offenbar vorschwebt. Dieses Produkt ist allerdings Antikommutativ, was der Grund ist, weshalb keine Potenzen wie ^3) im Resultat vorkommen, sondern jedes Differential nur einmal. Das ganze läuft unter der Bezeichnung "äußere Algebra" oder Graßmann-Algebra. Die wird einem aber im 1. Semester wahrscheinlich nicht begegnen. im Resultat vorkommen, sondern jedes Differential nur einmal. Das ganze läuft unter der Bezeichnung "äußere Algebra" oder Graßmann-Algebra. Die wird einem aber im 1. Semester wahrscheinlich nicht begegnen. |
|
 |
wasoren
Gast
|
 wasoren Verfasst am: 25. Nov 2015 22:11 Titel: wasoren Verfasst am: 25. Nov 2015 22:11 Titel: |
 |
|
Erst mal danke für die hilfreiche und ausführliche Antwort!
| index_razor hat Folgendes geschrieben: | | Die sphärischen Koordinaten sind schon orthogonal, aber nicht normiert. |
Wenn ich es richtig kenne, gibt es auch im sphärischen KOOS die Möglichkeit an einem Punkt P eine neue lokale Basis zu definieren, die dann eine ONB ist mit normierten Einheits-Vektoren, die in r, phi, theta Richtung zeigen. (tangential zu den Koordinatenlinien, die sie beschreiben; also phi beschreibt einen Kreis, dann ist einheitsvektor_phi die Tangente an diesem Kreis vom Punkt P)
Zum Verständnis: Stimmt das soweit?
Aber wieso sind die sphärischen Koord. denn orthogonal?
Wenn ich mir einen Punkt auf der Erde (z.B. geografisch in Deutschland) vorstelle, verstehe ich, dass R senkrecht zum von theta beschriebenen Großkreis steht (Normale am Kreis geht durch den Ursprung = das ist gerade der Radius). Aber: der kleinere zum Äquator parallele Kreis, der von phi beschrieben wird, da sehe ich keine Rechtwinkligkeit, sondern gerade den Winkel theta zum theta-Kreis bzw pi/2-theta zur R-Linie... , z.B. am Äquator ... oder ich verstehe: der phi-Kreis zeigt auf einen zu bzw. weg und damit ist er rechtwinklig zu den anderen beiden? Also bilden die Einheitsvektoren e_r, e_phi, e_theta eine (lokale, am Pkt P) ONB.
Zu den weiteren Überlegungen habe ich folgendes berechnet:

Nun sagst du, dass Produkt ist antikommutativ, also wenn ich recht verstehe gilt a*b = -b*a (warum?)
Wenn ich mir dxdydz als kleinen Quader vorstelle, ergibt antikommutativität für mich keinen Sinn, also versehe nicht, warum dx*dy*dz nicht gleich dV ?
Für die Berechnung zu dV = dxdydz hätte ich somit als ersten Summanden
^2\ +\ ...)
Viele Grüße |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 26. Nov 2015 09:29 Titel: index_razor Verfasst am: 26. Nov 2015 09:29 Titel: |
 |
|
| wasoren hat Folgendes geschrieben: | Erst mal danke für die hilfreiche und ausführliche Antwort!
| index_razor hat Folgendes geschrieben: | | Die sphärischen Koordinaten sind schon orthogonal, aber nicht normiert. |
Wenn ich es richtig kenne, gibt es auch im sphärischen KOOS die Möglichkeit an einem Punkt P eine neue lokale Basis zu definieren, die dann eine ONB ist mit normierten Einheits-Vektoren, die in r, phi, theta Richtung zeigen. (tangential zu den Koordinatenlinien, die sie beschreiben; also phi beschreibt einen Kreis, dann ist einheitsvektor_phi die Tangente an diesem Kreis vom Punkt P)
Zum Verständnis: Stimmt das soweit?
|
Ja. Du beschreibst also eine orthonormale Basis, deren Vektoren tangential zu den sphärischen Koordinatenlinien liegen. Wieso wunderst du dich dann darüber, daß die sphärischen Koordinaten orthogonal sind?
| Zitat: |
Aber wieso sind die sphärischen Koord. denn orthogonal?
Wenn ich mir einen Punkt auf der Erde (z.B. geografisch in Deutschland) vorstelle, verstehe ich, dass R senkrecht zum von theta beschriebenen Großkreis steht (Normale am Kreis geht durch den Ursprung = das ist gerade der Radius). Aber: der kleinere zum Äquator parallele Kreis, der von phi beschrieben wird, da sehe ich keine Rechtwinkligkeit, sondern gerade den Winkel theta zum theta-Kreis bzw pi/2-theta zur R-Linie... , z.B. am Äquator ... oder ich verstehe: der phi-Kreis zeigt auf einen zu bzw. weg und damit ist er rechtwinklig zu den anderen beiden?
|
Der Beschreibung kann ich nicht ganz folgen. (Was bedeutet es, daß "ein Kreis auf einen zu bzw. wegzeigt"?)
phi und theta beschreiben Längen- und Breitenkreise auf der Sphäre r=const. Diese Kreise schneiden sich im rechten Winkel auf der Kugeloberfläche. Die zugehörigen Basisvektoren sind die Tangenten an diese Koordinatenlinien und stehen folglich senkrecht aufeinander. r steht senkrecht auf der gesamten Fläche, also insbesondere senkrecht zur Längen- und Breitenrichtung.
| Zitat: |
Zu den weiteren Überlegungen habe ich folgendes berechnet:

|
Ja, das stimmt.
| Zitat: |
Nun sagst du, dass Produkt ist antikommutativ, also wenn ich recht verstehe gilt a*b = -b*a (warum?)
|
Aus demselben Grund, aus dem eine Determinante beim Vertauschen zweier Spalten das Vorzeichen wechselt. Eine Determinante kannst du dir vorstellen als ein antisymmetrisches Produkt aus n Vektoren.
Der Sinn dieses Produkts ist aus linearen Größen wie  durch Multiplikation Flächen- und Volumenmaße herzustellen. Diese linearen Größen sind aber gerichtet und durch Multiplikation Flächen- und Volumenmaße herzustellen. Diese linearen Größen sind aber gerichtet und 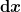 ist nicht gleich ist nicht gleich  . Das Produkt von zwei dieser Größen liefert also ebenfalls ein gerichtetes (oder orientiertes) Flächenmaß und das Produkt eines solchen Flächenmaßes mit einem weiteren Vektor liefert ein orientiertes Volumenmaß. Die Orientierung ist durch die Reihenfolge der Faktoren bestimmt. . Das Produkt von zwei dieser Größen liefert also ebenfalls ein gerichtetes (oder orientiertes) Flächenmaß und das Produkt eines solchen Flächenmaßes mit einem weiteren Vektor liefert ein orientiertes Volumenmaß. Die Orientierung ist durch die Reihenfolge der Faktoren bestimmt.
| Zitat: |
Wenn ich mir dxdydz als kleinen Quader vorstelle, ergibt antikommutativität für mich keinen Sinn, also versehe nicht, warum dx*dy*dz nicht gleich dV ?
|
Doch, dV=dx dy dz=dy dz dx = -dy dx dz = - dx dz dy = .....
Warum ergibt das keinen Sinn? Denke daran, daß alle Größen -- Richtungen, Flächen, Volumina -- eine Orientierung aufweisen.
| Zitat: |
Für die Berechnung zu dV = dxdydz hätte ich somit als ersten Summanden
^2\ +\ ...)
|
Das ist falsch gerechnet. In dem Produkt dx dy dz kommen nur Produkte aus drei Differentialen vor. Im ersten Summand fehlt noch dz.
Ein Volumen kannst du außerdem nur aus drei unabhängigen Richtungen wie Länge, Breite und Höhe zusammensetzen. Drei Richtungen die innerhalb einer Ebene oder sogar auf derselben Gerade liegen, spannen kein Volumen auf, oder besser gesagt, spannen sie einen entarteten Quader vom Volumen null auf. Deshalb ist ^3 = (\dd r)^2\dd\phi = ... = 0.)
Noch ein Hinweis zur Notation: In diesem Zusammenhang ist es üblich das äußere Produkt durch das Symbol  zu Kennzeichnen also zu Kennzeichnen also  zu schreiben. Wir haben das bis jetzt nicht getan und es ist für orthogonale Größen, wie zu schreiben. Wir haben das bis jetzt nicht getan und es ist für orthogonale Größen, wie  auch nicht unbedingt notwendig, da das einzig geläufige alternative Produkt, das Skalarprodukt, für diese Größen sowieso verschwindet. auch nicht unbedingt notwendig, da das einzig geläufige alternative Produkt, das Skalarprodukt, für diese Größen sowieso verschwindet. |
|
 |
wasoren
Gast
|
 wasoren Verfasst am: 30. Nov 2015 00:28 Titel: wasoren Verfasst am: 30. Nov 2015 00:28 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Im ersten Summand fehlt noch dz. |
Stimmt, habe nur den ersten Summanden von dx mit dem ersten von dy multipliziert.
| index_razor hat Folgendes geschrieben: | Ein Volumen kannst du außerdem nur aus drei unabhängigen Richtungen wie Länge, Breite und Höhe zusammensetzen. Drei Richtungen die innerhalb einer Ebene oder sogar auf derselben Gerade liegen, spannen kein Volumen auf, oder besser gesagt, spannen sie einen entarteten Quader vom Volumen null auf. Deshalb ist ^3 = (\dd r)^2\dd\phi = ... = 0.) |
Heißt das, alle Terme wo eines der Differentiale dr,dphi,dtheta mehr als einmal vorkommt, verschwindet?
Also nehmen wir den Term mir dr bei dx, den Term mit dphi von dy und den Term mit dtheta von dz.
Dann gibt es aber folgende Möglichkeiten (denke mal, die muss man alle aufsummieren):
Wähle von dx einen beliebigen Summanden (also den mit dr, dphi oder dtheta) == 3 Möglichkeiten
Wähle von dy einen Summanden, dessen Differential noch nicht genutzt wurde == 2 Möglichkeiten
Wähle von dz den Summanden, dessen Differential noch nicht genutzt wurde (falls dr,dtheta schon genutzt wurde wäre das hier dphi, aber dann verschwidet der Ausdruck), also insgesamt 6 Möglichkeiten, von denen die mit dphi für den dz-Term wegfällt, also ein Term mit 5 Summanden. Ist zwar noch nicht der kurze Ausdruck, der am Ende rauskommen soll, vielleicht vereinfachen?!
Ich erhalte:
 + \cos ^2\theta\sin\theta( \cos^2\phi -\sin^2\phi )) \ \dd r\dd \phi\dd \theta)
Wie geht es weiter... Den Ausdruck, wo ich r² ausgeklammert habe, müsste ja einfach nur sin(theta) ergeben... |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8583
|
 jh8979 Verfasst am: 30. Nov 2015 00:36 Titel: jh8979 Verfasst am: 30. Nov 2015 00:36 Titel: |
 |
|
| wasoren hat Folgendes geschrieben: |
Ich erhalte:
 + \cos ^2\theta\sin\theta( \cos^2\phi -\sin^2\phi )) \ \dd r\dd \phi\dd \theta)
Wie geht es weiter... Den Ausdruck, wo ich r² ausgeklammert habe, müsste ja einfach nur sin(theta) ergeben... |
Das ist in der Tat nicht richtig (da kommt nicht sin(theta) raus).
Du hast Dich bei den Vorzeichen vertan. Denk dran dass dr^dtheta = - dtheta^dr.
(Ich bin zu faul Latex zu schreiben ^ ist das antisymmetrische wedge-Produkt von oben nicht "hoch".) |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 30. Nov 2015 09:47 Titel: index_razor Verfasst am: 30. Nov 2015 09:47 Titel: |
 |
|
| wasoren hat Folgendes geschrieben: |
| index_razor hat Folgendes geschrieben: | Ein Volumen kannst du außerdem nur aus drei unabhängigen Richtungen wie Länge, Breite und Höhe zusammensetzen. Drei Richtungen die innerhalb einer Ebene oder sogar auf derselben Gerade liegen, spannen kein Volumen auf, oder besser gesagt, spannen sie einen entarteten Quader vom Volumen null auf. Deshalb ist ^3 = (\dd r)^2\dd\phi = ... = 0.) |
Heißt das, alle Terme wo eines der Differentiale dr,dphi,dtheta mehr als einmal vorkommt, verschwindet?
|
Ja genau das heißt es. Ich hoffe es ist anschaulich klar geworden, warum das so sein muß. Algebraisch ist es eine direkte Folge der Antisymmetrie des Produktes aus zwei Koordinatendifferentialen.
| Zitat: |
Also nehmen wir den Term mir dr bei dx, den Term mit dphi von dy und den Term mit dtheta von dz.
Dann gibt es aber folgende Möglichkeiten (denke mal, die muss man alle aufsummieren):
|
Du mußt dieses Produkt nach dem Distributivgesetz entwickeln, ja. Dieses Gesetz gilt für ausnahmslos alle Operation, die man normalerweise als "Produkt" bezeichnet.
| Zitat: |
Wähle von dx einen beliebigen Summanden (also den mit dr, dphi oder dtheta) == 3 Möglichkeiten
Wähle von dy einen Summanden, dessen Differential noch nicht genutzt wurde == 2 Möglichkeiten
Wähle von dz den Summanden, dessen Differential noch nicht genutzt wurde (falls dr,dtheta schon genutzt wurde wäre das hier dphi, aber dann verschwidet der Ausdruck), also insgesamt 6 Möglichkeiten, von denen die mit dphi für den dz-Term wegfällt, also ein Term mit 5 Summanden. Ist zwar noch nicht der kurze Ausdruck, der am Ende rauskommen soll, vielleicht vereinfachen?!
|
Insgesamt müßten es vier Summanden sein: zwei Summanden mit jeweils einem Differential aus dx und dy für jedes der zwei, von denen dz selbst abhängt.
Die Regel, die du beschreibst ist aber im Prinzip richtig. (Auf einen Vorzeichenfehler wurdest du ja schon hingewiesen.) Vielleicht erkennst du darin dieselbe Art von Buchhaltung (inklusive der Vorzeichen), die man beim Berechnen von Determinanten nach dem Laplaceschen Entwicklungssatz anwendet. Das Resultat ist ja auch genau identisch mit der Jacobi-Determinante. |
|
 |
|
|















