| Autor |
Nachricht |
Decsis
Anmeldungsdatum: 22.10.2012
Beiträge: 12
|
 Decsis Verfasst am: 01. Nov 2014 17:44 Titel: Limes in der Formel der Winkelgeschwindigkeit |
 |
|
Hallo zusammen, in unserer Vorlesung wurde die Winkelgeschwindigkeit wie folgt definiert:
wobei  der Drehwinkel in rad ist.
Mir leuchtet soweit ein, dass die Winkelgeschwindigkeit die Änderung des Winkels durch die dabei verstrichene Zeit ist. Ich muss sagen, dass wir gerade erst mit der Infinitesimalrechnung angefangen haben, doch weshalb würde es Sinn machen, delta t gegen 0 gehen zu lassen? Ich meine, wenn keine Zeit verstreicht, kann sich doch auch der Winkel nicht ändern? |
|
 |
jumi
Gast
|
| jumi Verfasst am: 01. Nov 2014 18:39 Titel: |
|
|
Zuerst lernt man dies bei der geradlinigen Geschwindigkeit:
Durchschnittsgeschwindigkeit = 
Momentangeschwindigkeit = 
Wenn du das verstehst, dann bei Winkelgeschwindigkeit analog anwenden. |
|
|
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
| franz Verfasst am: 01. Nov 2014 20:27 Titel: Re: Limes in der Formel der Winkelgeschwindigkeit |
|
|
| Decsis hat Folgendes geschrieben: | |
 |
|
|
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
| Jayk Verfasst am: 02. Nov 2014 01:16 Titel: Re: Limes in der Formel der Winkelgeschwindigkeit |
|
|
| Decsis hat Folgendes geschrieben: | | Mir leuchtet soweit ein, dass die Winkelgeschwindigkeit die Änderung des Winkels durch die dabei verstrichene Zeit ist. Ich muss sagen, dass wir gerade erst mit der Infinitesimalrechnung angefangen haben, doch weshalb würde es Sinn machen, delta t gegen 0 gehen zu lassen? Ich meine, wenn keine Zeit verstreicht, kann sich doch auch der Winkel nicht ändern? |
Hattest du denn in der Schule Mathe? In der zehnten, spätestens in der elften Klasse lernt man doch, was ein Grenzwert ist. Aufbauend darauf wird in der Oberstufe (normalerweise in der elften Klasse) die Ableitung definiert, allgemein für eine Funktion f von x bei x0 durch eine oder beide der folgenden äquivalenten Definitionen
 = \lim_{x \to x_0} \frac{f(x)-f(x_0)}{x-x_0} = \lim_{h \to 0} \frac{f(x_0 + h ) - f(x_0 )}{h})
(letzteres wird anscheinend gerne als die "h-Methode" eingeführt^^)
Nichts Anderes liegt hier vor:
 = \dot \phi (t ) = \lim_{\tau \to t} \frac{\phi (\tau) - \phi (t)}{\tau - t} = \lim_{\Delta t \to 0} \frac{\phi (t + \Delta t) - \phi (t)}{\Delta t}) .
Der Zähler wird dann (nicht wirklich richtig, nicht wirklich falsch) als  notiert. So eine Definition versteht man auch nur, wenn man weiß, was gemeint ist. Wichtig ist, dass von 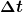 abhängt: Wenn das eine gegen null geht, geht auch das andere gegen null (Stetigkeit vorausgesetzt), aber das Verhältnis wird (Differenzierbarkeit vorausgesetzt) einem festen Wert entgegenstreben. Man kann sich die Ableitung auch als "beste Linearisierung" vorstellen (viele Physiker würden das sicher mit dem Verschwinden quadratischer und höherer Terme der Taylor-Entwicklung erklären, aber die Kausalität ist genau anders herum und diese Tatsache ist viel fundamentaler). Die Eigenschaft, dass der Restterm  - \phi (t) - \Delta t \cdot \omega (t)}{\Delta t}) gegen null geht, benutzt man auch in Analysis 2, um Differenzierbarkeit in mehreren Dimensionen und das (totale) Differential zu definieren, im Endimensionalen ist es natürlich genauso richtig (der Beweis ist auch nicht schwer). Das bedeutet, dass sich die Funktion ) in der Nähe von 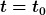 an eine Gerade mit dem Anstieg ) schmiegt.
Man hätte auch  schreiben können. Das wäre fast genauso richtig, aber dann müsste man zeigen, dass die Definition sinnvoll ist, was schon Analysis 2 Methoden erfordert (Satz von der impliziten/inversen Funktion). Eine Funktion ist so definiert, dass sie jedem Argument genau einen Funktionswert zuordnet (zu jedem Zeitpunkt gibt es genau einen Drehwinkel). Die Umkehrung gilt nicht: Ein Drehwinkel kann zu mehreren Zeitpunkten eingenommen werden. Katastrophal wird es für den Fall, dass  lokal konstant ist. Um solchen Problem zu entgehen, lässt man die Differenz des Arguments gegen null gehen. |
|
|
|
|
Registrieren
Login
FAQ
Suchen
