Startseite
 
 
Fragen
 
Suchen
 
Formeleditor
 
Über Uns
 
 
  RegistrierenRegistrieren   LoginLogin   FAQFAQ    SuchenSuchen   
Normalisierung Wellenfunktion Partikel
 
Neue Frage »
Antworten »
    Foren-Übersicht -> Quantenphysik
Autor Nachricht
Starborne



Anmeldungsdatum: 03.10.2014
Beiträge: 4
Beitrag Starborne Verfasst am: 03. Okt 2014 17:33    Titel: Normalisierung Wellenfunktion Partikel Antworten mit Zitat
Hallo zusammen!

Leider bin ich auf ein Problem bei der Normalisierung einer gegebenen Wellenfunktion gestossen.

Die Aufgabe lautet: Ein Partikel habe Wellenfunktion Psi (siehe unten), wobei r den Abstand des Partikels zum Mittelpunkt sei. Der Koeffizient A soll mithilfe der Normalisierungsbedingung gefunden werden.

Hinweis: dV soll mithilfe von dr und des Volumens einer Kugel ausgedrückt weden.



Mein Ansatz also:



Weiter:



Ich wandle dV In Kugelkoordinaten um:



und dann stehe ich vor einem Dreifachintegral mit Winkel Theta, Phi und r. Würde ich dieses Auflösen, erhielte ich eine von r-abhängige "Lösung" die mich mehr verwirrt als erfreut!

Habe ich mich hier schwer verlaufen bei der Transformation in Kugelkoordinaten, oder soll ich so weiterfahren? Wenn ja, kann mir jemand dabei weiterhelfen?

Danke bereits im voraus!

Gruss,

Starborne
index_razor



Anmeldungsdatum: 14.08.2014
Beiträge: 3259
Beitrag index_razor Verfasst am: 03. Okt 2014 18:27    Titel: Re: Normalisierung Wellenfunktion Partikel Antworten mit Zitat
Starborne hat Folgendes geschrieben:
Würde ich dieses Auflösen, erhielte ich eine von r-abhängige "Lösung" die mich mehr verwirrt als erfreut!


Warum? Wenn das Volumen, auf das 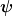normiert werden soll eine endliche Kugel ist, hängt die Normierungskonstante im allgemeinen vom Radius der Kugel ab. Allerdings vermute ich mal, die Wellenfunktion soll über den gesamten Raum normiert werden. Kann das sein? Dann mußt du nur noch den Grenzübergang ausführen.

Was hast du denn bisher raus?
Dirac
Gast
Beitrag Dirac Verfasst am: 03. Okt 2014 18:51    Titel: Antworten mit Zitat
Das Dreifach-Integral lautet doch



Jedes Integral ist einzeln lösbar.
Starborne



Anmeldungsdatum: 03.10.2014
Beiträge: 4
Beitrag Starborne Verfasst am: 03. Okt 2014 19:25    Titel: Antworten mit Zitat
Dirac hat Folgendes geschrieben:
Das Dreifach-Integral lautet doch



Jedes Integral ist einzeln lösbar.


Du wählst hier als Grenzen für r: 0 bis unendlich. Wenn ich das einsetze erhalte ich:



wobei sich dann 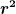wegstreicht und ich über die e-Funktion integriere. Dann erhalte ich für den ganzen Term aber unendlich, sobald ich die Grenzen einsetze?

Als Randbemerkung: Ich befasse mich erst seit knapp 3 Wochen mit der Quantenmechanik. Somit sind mir die meisten Konzepte noch nicht sehr vertraut.

Danke für eure Antworten!
index_razor



Anmeldungsdatum: 14.08.2014
Beiträge: 3259
Beitrag index_razor Verfasst am: 03. Okt 2014 19:35    Titel: Antworten mit Zitat
Starborne hat Folgendes geschrieben:

Du wählst hier als Grenzen für r: 0 bis unendlich. Wenn ich das einsetze erhalte ich:



wobei sich dann 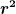wegstreicht und ich über die e-Funktion integriere. Dann erhalte ich für den ganzen Term aber unendlich, sobald ich die Grenzen einsetze?


Nein, da kommt was endliches raus.

P.S.:

Starborne



Anmeldungsdatum: 03.10.2014
Beiträge: 4
Beitrag Starborne Verfasst am: 03. Okt 2014 19:53    Titel: Antworten mit Zitat
Zitat:
Nein, da kommt was endliches raus.

P.S.:



Da hast du natürlich recht.

sollte das Ergebnis meiner Meinung nach sein.

Also zusammenfassend habe ich dann:



Bin ich bis hier hin korrekt vorgegangen?
index_razor



Anmeldungsdatum: 14.08.2014
Beiträge: 3259
Beitrag index_razor Verfasst am: 03. Okt 2014 20:10    Titel: Antworten mit Zitat
Das Winkelintegral sollte insgesamt eigentlich 4 pi ergeben. Das ist der gesamte Raumwinkel. Das heißt, es sollte



rauskommen. Ansonsten ist, denke ich, alles richtig.
Starborne



Anmeldungsdatum: 03.10.2014
Beiträge: 4
Beitrag Starborne Verfasst am: 03. Okt 2014 20:50    Titel: Antworten mit Zitat
index_razor hat Folgendes geschrieben:
Das Winkelintegral sollte insgesamt eigentlich 4 pi ergeben. Das ist der gesamte Raumwinkel. Das heißt, es sollte



rauskommen. Ansonsten ist, denke ich, alles richtig.


Alles klar, da muss ich wohl den sinus übersehen haben im Integral. Dann bedanke ich an diesem Punkt ganz herzlich bei euch für die tatkräftie Unterstützung.

Ein schönes Wochenende!

Starborne
Neue Frage »
Antworten »
    Foren-Übersicht -> Quantenphysik

Verwandte Themen - die Neuesten
 Themen   Antworten   Autor   Aufrufe   Letzter Beitrag 
Keine neuen Beiträge Kollaps der Wellenfunktion und Heisenberg-Unschärferelation 3 Daniel444 1705 07. Nov 2023 09:21
TomS Letzten Beitrag anzeigen
Keine neuen Beiträge Eine einzige Wellenfunktion? 96 Jupp_@ 8151 26. Jul 2023 16:19
Jupp_@ Letzten Beitrag anzeigen
Keine neuen Beiträge Radiale Wellenfunktion 2 frage1 1092 26. Sep 2022 22:08
frage1 Letzten Beitrag anzeigen
Keine neuen Beiträge Analyse der Wellenfunktion 17 frage1 1359 17. Sep 2022 07:22
frage1 Letzten Beitrag anzeigen
Keine neuen Beiträge Potential zur Wellenfunktion 1 liph27 771 04. Jul 2022 13:24
TomS Letzten Beitrag anzeigen
 

Verwandte Themen - die Größten
 Themen   Antworten   Autor   Aufrufe   Letzter Beitrag 
Dieses Thema ist gesperrt, du kannst keine Beiträge editieren oder beantworten. Wellenfunktion: Schreibweise 277 terminus 8885 29. Mai 2022 22:03
TomS Letzten Beitrag anzeigen
Keine neuen Beiträge Eine einzige Wellenfunktion? 96 Jupp_@ 8151 26. Jul 2023 16:19
Jupp_@ Letzten Beitrag anzeigen
Keine neuen Beiträge Kollaps der Wellenfunktion 42 bip 9817 02. Mai 2022 13:45
TomS Letzten Beitrag anzeigen
Keine neuen Beiträge Orthonormale Wellenfunktion 35 frage1 2031 10. Sep 2022 16:40
TomS Letzten Beitrag anzeigen
Keine neuen Beiträge Wellenlänge nach Kopenhagener Deutung, Wellenfunktion 26 Gast 6680 24. Jul 2012 17:20
TomS Letzten Beitrag anzeigen
 

Verwandte Themen - die Beliebtesten
 Themen   Antworten   Autor   Aufrufe   Letzter Beitrag 
Keine neuen Beiträge Herleitung der Wellenfunktion für stehende Wellen 7 Ardente04 16226 13. Jun 2011 21:16
schnudl Letzten Beitrag anzeigen
Keine neuen Beiträge Normierungskonstante einer Wellenfunktion berechnen 5 Rafael91 14235 19. Feb 2012 15:12
Rafael91 Letzten Beitrag anzeigen
Keine neuen Beiträge Einheit Wellenfunktion 15 mzh 9867 28. Jan 2011 14:09
Chillosaurus Letzten Beitrag anzeigen
Keine neuen Beiträge Kollaps der Wellenfunktion 42 bip 9817 02. Mai 2022 13:45
TomS Letzten Beitrag anzeigen
Dieses Thema ist gesperrt, du kannst keine Beiträge editieren oder beantworten. Wellenfunktion: Schreibweise 277 terminus 8885 29. Mai 2022 22:03
TomS Letzten Beitrag anzeigen
 




 
© 2004-2021 bei Physikerboard.de | Kontakt | Jugendschutz | Nutzungsbedingungen