| Autor |
Nachricht |
Winder
Anmeldungsdatum: 19.07.2012
Beiträge: 1
|
 Winder Verfasst am: 19. Jul 2012 20:56 Titel: Wellenlänge nach Kopenhagener Deutung, Wellenfunktion Winder Verfasst am: 19. Jul 2012 20:56 Titel: Wellenlänge nach Kopenhagener Deutung, Wellenfunktion |
 |
|
Meine Frage:
die Wellenfunktion (Psi) gibt in 3D eine Wahrscheinlichkeitverteilung möglicher Trefferpunkte entlang einer Bewegungslinie. Die Frage betrifft die dazu gehörende Wellenlänge: wird sie für Photonen nach relativistischem Dppler und für Ruhemasseteilchen (RmT) nach de Broggli berechnet und auf Psi angewendet? Oder gibt es eine unabhängige Methode in QM diese Wellenlänge zu berechnen?
Meine Ideen:
ich denke bislang, dass es wohl so ist |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 19. Jul 2012 21:05 Titel: TomS Verfasst am: 19. Jul 2012 21:05 Titel: |
 |
|
Die Wellenfunktion ergibt sich im Rahmen der nichtrelativistischen Quantenmechanik aus der Schrödingergleichung, üblicherweise für ein (oder mehrere) Teilchen in einem äußeren Feld (elektrisches Potential, Magnetfeld, ...). D.h. sie wird berechnet.
Im Rahmen der rel. QM kommt stattdessen die Diarc- oder die Klein-Gordon-Gleichung zur Anwendung, aber da ist die Interpretation nicht immer sinnvoll möglich.
Für Photonen kann man das nicht durchführen; Licht als el.-mag Welle genügt nur den klassischen Maxwellgleichungen; Photonen als quantisierte Schwingungen sind dagegen mittels der Quantenfeldtheorie zu beschreiben. Daher ist die "einfache" Gleichung E = hf nicht aus einer einfachen Theorie ableitbar, wie dies für nicht-rel. QM möglich ist.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
winter
Anmeldungsdatum: 19.07.2012
Beiträge: 70
Wohnort: Berlin
|
 winter Verfasst am: 19. Jul 2012 21:54 Titel: winter Verfasst am: 19. Jul 2012 21:54 Titel: |
 |
|
leider reicht es mir nicht als Antwort,
gut, trennen wir Photone für später ab, und reden von RmTs
relativistische de Broggli Wellenlänge aus V und m berechnen und in der Wellenfunktion einsetzen?
d.h. auch, in Bewegungsrichtung sagt die Wellenlänge schon mal die wichtigste Ortsverteilung aus, und Psi ergänzt es dazu noch mit der 3D Verteilung? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 19. Jul 2012 22:21 Titel: TomS Verfasst am: 19. Jul 2012 22:21 Titel: |
 |
|
| winter hat Folgendes geschrieben: | | relativistische de Broggli Wellenlänge aus V und m berechnen und in der Wellenfunktion einsetzen? |
Andersherum: Wellenfunktion berechnen und daraus die Wellenlänge ableiten
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Uriezzo
Anmeldungsdatum: 15.09.2011
Beiträge: 281
Wohnort: Großostheim
|
 Uriezzo Verfasst am: 20. Jul 2012 08:41 Titel: Re: Wellenlänge nach Kopenhagener Deutung, Wellenfunktion Uriezzo Verfasst am: 20. Jul 2012 08:41 Titel: Re: Wellenlänge nach Kopenhagener Deutung, Wellenfunktion |
 |
|
| Winder hat Folgendes geschrieben: | Meine Frage:
die Wellenfunktion (Psi) gibt in 3D eine Wahrscheinlichkeitverteilung möglicher Trefferpunkte entlang einer Bewegungslinie. Die Frage betrifft die dazu gehörende Wellenlänge: wird sie für Photonen nach relativistischem Dppler und für Ruhemasseteilchen (RmT) nach de Broggli berechnet und auf Psi angewendet? Oder gibt es eine unabhängige Methode in QM diese Wellenlänge zu berechnen? |
In der Regel lassen sich realistischen Zuständen für Teilchen, wie ich sie in der QM z.B. aus der Schrödingergleichung berechne, gar keine Wellenlänge eindeutig zuordnen.
Das kann man theoretisch nur, wenn das Teilchen sich in einem Impulseigenzustand . befindet, also einem Zustand bei dem der Impuls des Teilchens befindet, also einem Zustand bei dem der Impuls des Teilchens 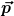 eindeutig bestimmt ist. Dann ergibt sich die Wellenlänge aus den bekannten Formeln. Ein Teilchen in einem Impulseigenzustand wäre über den gesamten Raum "verschmiert" (die Wellenfunktion, also der Zustand des Teilchens in Ortsdarstellung, entspräche einer unendlich ausgedehnten harmonischen Welle: eindeutig bestimmt ist. Dann ergibt sich die Wellenlänge aus den bekannten Formeln. Ein Teilchen in einem Impulseigenzustand wäre über den gesamten Raum "verschmiert" (die Wellenfunktion, also der Zustand des Teilchens in Ortsdarstellung, entspräche einer unendlich ausgedehnten harmonischen Welle:
 \sim e^{i\vec{k}\vec{x}}
<br />
)
).
Impulseigenzustände sind dementsprechend idealisierte Zustände, die in der Realität eigentlich nicht auftreten. Auch mathematisch bereiten sie Probleme, da man einen Impulseigenzustand nicht so ohne weiteres auf 1 normieren kann.
Realistische Zustände setzen sich aus einer Überlagerung von beliebig vielen Impulseigenzuständen zusammen:
 \left| \vec{p} \right>
<br />
)
Dementsprechend kann ich ihnen auch nicht eindeutig eine Wellenlänge zuordnen. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 20. Jul 2012 08:58 Titel: jh8979 Verfasst am: 20. Jul 2012 08:58 Titel: |
 |
|
|
Wenn man schon so klugscheissert, sollte man auch verstehen was man da eigentlich sagt: selbst wenn ich den Zustand nur als Wellenpaket abgeben kann, kann ich ja troztdem eine Wellenlaenge (in gewisser Genauigkeit) angeben.... |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 20. Jul 2012 09:08 Titel: Re: Wellenlänge nach Kopenhagener Deutung, Wellenfunktion TomS Verfasst am: 20. Jul 2012 09:08 Titel: Re: Wellenlänge nach Kopenhagener Deutung, Wellenfunktion |
 |
|
| Uriezzo hat Folgendes geschrieben: | In der Regel lassen sich realistischen Zuständen für Teilchen, wie ich sie in der QM z.B. aus der Schrödingergleichung berechne, gar keine Wellenlänge eindeutig zuordnen
...
Realistische Zustände setzen sich aus einer Überlagerung von beliebig vielen Impulseigenzuständen zusammen:
 \left| \vec{p} \right>
<br />
) |
Wenn nun A(p) eine Funktion mit einem sehr engen Peak ist, dann ist der Impuls und damit die Wellenlänge durch den Peak sehr genau (aber eben nicht exakt) definiert.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Uriezzo
Anmeldungsdatum: 15.09.2011
Beiträge: 281
Wohnort: Großostheim
|
 Uriezzo Verfasst am: 20. Jul 2012 09:20 Titel: Uriezzo Verfasst am: 20. Jul 2012 09:20 Titel: |
 |
|
| jh8979 hat Folgendes geschrieben: | | Wenn man schon so klugscheissert, sollte man auch verstehen was man da eigentlich sagt: selbst wenn ich den Zustand nur als Wellenpaket abgeben kann, kann ich ja troztdem eine Wellenlaenge (in gewisser Genauigkeit) angeben.... |
Es gibt keinen Grund, persönlich zu werden. Ich kann eben für ein Wellenpaket nicht mehr eindeutig eine Wellenlänge angeben, höchstens näherungsweise. Das weißt Du genauso gut wie ich. |
|
 |
winter
Anmeldungsdatum: 19.07.2012
Beiträge: 70
Wohnort: Berlin
|
 winter Verfasst am: 20. Jul 2012 11:45 Titel: keine Wellenlänge? winter Verfasst am: 20. Jul 2012 11:45 Titel: keine Wellenlänge? |
 |
|
das wäre eine Überraschung, denn dann ist uns die De Broglie Wellenlänge nutzlos?

es ist mir bewusst, dass die Wellenmathematik mit sich diese unendlichen Wellen bringt, aber das ist rein mathematisches Problem, physikalisch wiederlegbar... also muss interppretiert werden... die Wellenpackete ist ein Versuch, es zu "reparieren", mit dem Folgeproblem der eigentlich nicht existenten zusätzlich überlagerten Wellen und daher Wellenlängen (die alle existieren auch nicht)
also, nochmal, mit maximaler Einfachheit: es bewegt sich ein Elektron mit konstanter V durch den Raum (durch Trägheit), dazu gibt es De Broggli Wellenlänge, die jedoch nur den Abstand zwischen den Maxima der Welle angibt..
angenommen (was nicht möglich ist) ein Stoßpunkt wäre hinreichend genau bekannt, dann läuft nach dem Stoss die "Welle" nach De Broggli ab und man kann also einen Trefferpunkt statistisch vorhersagen: dieser wäre in der Nähe des Vielfachen der Wellenlänge + eine statistische Streuung um diesen Punkt dreidimensional verteilt. Je dichter an Wellenberg umso wahrscheinlicher der Treffer. Dann ist die De Broglie Wellenlänge von Nutzen... |
|
 |
winter
Anmeldungsdatum: 19.07.2012
Beiträge: 70
Wohnort: Berlin
|
 winter Verfasst am: 20. Jul 2012 11:50 Titel: winter Verfasst am: 20. Jul 2012 11:50 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | winter hat Folgendes geschrieben: | | relativistische de Broggli Wellenlänge aus V und m berechnen und in der Wellenfunktion einsetzen? |
Andersherum: Wellenfunktion berechnen und daraus die Wellenlänge ableiten |
ok, aber wie ist dann die Information in die Wellenfunktion hinein gelangt? m und V? |
|
 |
Uriezzo
Anmeldungsdatum: 15.09.2011
Beiträge: 281
Wohnort: Großostheim
|
 Uriezzo Verfasst am: 20. Jul 2012 12:12 Titel: Re: keine Wellenlänge? Uriezzo Verfasst am: 20. Jul 2012 12:12 Titel: Re: keine Wellenlänge? |
 |
|
| winter hat Folgendes geschrieben: | das wäre eine Überraschung, denn dann ist uns die De Broglie Wellenlänge nutzlos?
|
Nicht nutzlos, da es ja Zustände gibt, die näherungsweise Impulseigenzuständen gleichen, aber eben auch nicht so hilfreich wie einem in der Schule oft beigebracht wird.
Da lernt man nicht selten, dass man Teilchen eine Welle mit einer bestimmten Wellenlänge zuordnen kann und das ist meiner Meinung nach - auch wenn ich jetzt wieder Gefahr laufe der Klugscheißerei bezichtigt zu werden - nicht sehr hilfreich beim Verständnis der Quantenmechanik, sondern führt leider oft zu falschen Vorstellungen. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 20. Jul 2012 13:05 Titel: TomS Verfasst am: 20. Jul 2012 13:05 Titel: |
 |
|
| winter hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | winter hat Folgendes geschrieben: | | relativistische de Broggli Wellenlänge aus V und m berechnen und in der Wellenfunktion einsetzen? |
Andersherum: Wellenfunktion berechnen und daraus die Wellenlänge ableiten |
ok, aber wie ist dann die Information in die Wellenfunktion hinein gelangt? m und V? |
Durch Lösen der Wellengleichung.
Ganz allgemein gilt
 = 0)
In dem Operator H stecken Terme für eine "freie Wellengleichung" eines Quantenobjektes der Masse m sowie Wechselwirkungen mit äußeren el. und mag. Feldern. Dazu konstruiert man nun Lösung zu fester Energe E, d.h.
 )
sowie ggf. Wellenpakete als Überlagerung, d.h.
 = \int dE \,\phi(E)\,\psi_E(\vec{x},t) )
(bzw. noch weitere Summen und Integrale außer E, die ich hier der Einachheit halber weglasse)
Wenn diese Wellenpakete eine hinreichend scharf definierten Impuls haben, dann kann man dem Wellenpaket wiederum eine deBroglie-Wellenlänge zuordnen.
Zusammenfassend kann man derartige Wellenfunktionen also auf verschiedene Weise:
- durch Lösung der o.g. Gleichung
- durch Überlagerung, wobei dies i.A. keine Lösungen mehr sein werden
Letzteres entspricht der Realität, d.h. es gibt sicher keinen unendlich ausgedehnten Wellenzug exakt fester Frequenz, sondern nur mehr oder wneiger lokalisierte Wellenpakete, deren Frequenz sozusagen etwas unscharf ist.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 20. Jul 2012 15:53 Titel: jh8979 Verfasst am: 20. Jul 2012 15:53 Titel: |
 |
|
| Uriezzo hat Folgendes geschrieben: |
Es gibt keinen Grund, persönlich zu werden. Ich kann eben für ein Wellenpaket nicht mehr eindeutig eine Wellenlänge angeben, höchstens näherungsweise. Das weißt Du genauso gut wie ich. |
Sorry, sollte nicht persoenlich sein. Vllt war ich einfach schlecht drauf beim Schreiben. Kommt vor 
Trotzdem wissen wir beide, dass ein Wellenpaket im Impulsraum zwar zu keiner eindeutigen Wellenlaenge fuehrt, aber in der Realitaet in den meisten Faellen diese "Unschaerfe" in der Wellenlaenge herzlich egal ist. Darum fand ich Deinen Beitrag einfach wenig hilfreich... |
|
 |
winter
Anmeldungsdatum: 19.07.2012
Beiträge: 70
Wohnort: Berlin
|
 winter Verfasst am: 20. Jul 2012 19:01 Titel: winter Verfasst am: 20. Jul 2012 19:01 Titel: |
 |
|
http://www.matheboard.de/latex2png/latex2png.php?\left[i\frac{\partial}{\partial%20t}%20-%20H\right]%20\psi(\vec{x},t)%20=%200
ok, im Hamilton ist also auch vorgesehen, E Feld für die Wechselwirkung bereitzustellen. Aber wenn ich nun ein Teilchen im Raum ohne E- und B-Felder habe, nur homogene Gravitation. Dann muss doch allein die Ortsverteilung ausreichen? und die ist dann mit "Wellenbergen" nach de Broglie?
einfache Überlegung: wenn de Broglie und die aus Wellengleichung ermittelte Wellenlänge nicht gleich sind, dann laufen deren Orte wegen Gangunterschied hoffnungslos auseinander, je länger wir es treiben... das wären widersprüchliche Beschreibungen... man würde das Teilchen am falschen Ort erwarten |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 20. Jul 2012 19:27 Titel: TomS Verfasst am: 20. Jul 2012 19:27 Titel: |
 |
|
Man kann natürlich auch einen Hamiltonian mit Gravitationspotential betrachten, das ist kein Problem. Man kann auch (für ein Gravitationsfeld) zunächst ein Wellenpaket ansetzen und dessen zeitliche Entwicklung (d.h. Bewegung, Verbreiterung, Veränderung des Impulserwartungswertes, ...) bestimmen.
Ich verstehe aber nicht soi recht, was du mit "Dann muss doch allein die Ortsverteilung ausreichen" meinst.
Wenn man eine ebene Welle mit definierter Wellenlänge hat, dann hat diese überhaupt keinen "Ort"; die Wahrscheinlichkeit, das Teilchen irgendwo zu finden, ist gleichverteilt.
Was meinst du also mit "wenn de Broglie und die aus Wellengleichung ermittelte Wellenlänge nicht gleich sind, dann laufen deren Orte wegen Gangunterschied hoffnungslos auseinander"
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
winter
Anmeldungsdatum: 19.07.2012
Beiträge: 70
Wohnort: Berlin
|
 winter Verfasst am: 20. Jul 2012 20:30 Titel: winter Verfasst am: 20. Jul 2012 20:30 Titel: |
 |
|
Zitat: Wenn man eine ebene Welle mit definierter Wellenlänge hat, dann hat diese überhaupt keinen "Ort"; die Wahrscheinlichkeit, das Teilchen irgendwo zu finden, ist gleichverteilt.
ich habe wohl ein anderes Verständnis der Wahrscheinlichkeitsverteilung. Du meinst, nur weil wir Wellenmathematik anwenden, soll das Teilchen auch physikalisch "gleichzeitig" überall der Welle entlang sein?
ja, solch seltsame Interpretation fand ich öfters, z.B. die "Kugelwelle" (Aufenthaltswahrscheinlichkeit gemeint) eines Photons? Im Beispiel wartete man 1 Jahr, der Kugelradius wurde 1 Lichtsjahr, und dann hies es dass Teilchen sein überall und erst wenn wir es erwischen, hat es sich gerade entschieden, wo es sei, sodass dann eine Überlichtgeschwindigkeit für die Strecke von 2 Lichtjahren auftaucht? Aber das halte ich einfach für eine Überinterpretation der mathematischen Beschreibung. d.h. das einzelne Photon hat keine Kugelwelle, es ist nach seiner Emission bereits in bestimmter Richtung, nur wissen wir es nicht in welcher... Kugelwelle kann nur ein Haufen von Photonen bilden
deswegen ist auch meine Frage.. ich möchte letztens wissen, ob diese Wellenlänge aus der Wellenwahrscheinlichkeitsverteilung wie die De Brogliesche relativistisch zu berechnen ist
vielleicht ist noch der Grund für unsere Verständigungsschwierigkeit der, dass ich nicht weiss, wofür die Physiker diese Wellenfunktion verwenden? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 20. Jul 2012 21:32 Titel: TomS Verfasst am: 20. Jul 2012 21:32 Titel: |
 |
|
| winter hat Folgendes geschrieben: | | ich habe wohl ein anderes Verständnis der Wahrscheinlichkeitsverteilung. |
Dann hast du ein Problem ;-)
| winter hat Folgendes geschrieben: | | Du meinst, nur weil wir Wellenmathematik anwenden, soll das Teilchen auch physikalisch "gleichzeitig" überall der Welle entlang sein? |
Das habe ich nicht gesagt!
Ich sagte nicht: „Wenn man die Wellenmathematik anwendet …“ sondern „Wenn man eine ebene Welle mit definierter Wellenlänge hat …„
Das ist nun einmal so; eine unendlich ausgedehnte ebene Welle ist nicht lokalisiert; und umgekehrt ist ein lokalisiertes Wellenpaket eben keine ebene Welle.
| winter hat Folgendes geschrieben: | | ja, solch seltsame Interpretation fand ich öfters, … |
Ja, die Quantenmechanik ist seltsam – aber sie beschreibt die experimentellen Ergebnisse korrekt.
| winter hat Folgendes geschrieben: | | … z.B. die "Kugelwelle" (Aufenthaltswahrscheinlichkeit gemeint) eines Photons? Im Beispiel wartete man 1 Jahr, der Kugelradius wurde 1 Lichtsjahr, und dann hies es dass Teilchen sein überall und erst wenn wir es erwischen, hat es sich gerade entschieden, wo es sei, sodass dann eine Überlichtgeschwindigkeit für die Strecke von 2 Lichtjahren auftaucht? |
Das verstehe ich nicht
| winter hat Folgendes geschrieben: | | … das einzelne Photon hat keine Kugelwelle, es ist nach seiner Emission bereits in bestimmter Richtung, nur wissen wir es nicht in welcher... |
das ist nachweislich falsch (Stichwort: verborgene Variablen, Bellsches Theorem)
| winter hat Folgendes geschrieben: | | ich möchte letztens wissen, ob diese Wellenlänge aus der Wellenwahrscheinlichkeitsverteilung wie die De Brogliesche relativistisch zu berechnen ist |
Wie mehrfach erwähnt. Gegeben sei eine Wellenfunktion als Lösung der Schrödingergleichung oder eine allgemeine Überlagerung von Lösungen. Aus einem derartigen Wellenpaket berechnet man den Impulserwartungswert und daraus wiederum die deBroglie-Wellenlänge. Letzteres ist jedoch nur sinnvoll, wenn die Breite der Wellenfunktion im Impulsraum klein ist, wenn also in einem gewissen Raumbereich näherungsweise eine ebene Welle vorliegt. Für gut lokalisierte Wellenpakete im Ortsraum kann man die o.g. Rechnung zwar durchführen, die Interpretation ist jedoch wenig aussagekräftig.
| winter hat Folgendes geschrieben: | | vielleicht ist noch der Grund für unsere Verständigungsschwierigkeit der, dass ich nicht weiss, wofür die Physiker diese Wellenfunktion verwenden? |
Die Wellenfunktion ist ein mathematischer Ausdruck, aus dem sich die Gesamtheit der „Eigenschaften“ eines Quantensystems ableiten lässt. Sie ist eine von mehreren äquivalenten Darstellungen, man muss nicht zwingend mit Wellenfunktionen im Ortsraum arbeiten, kann diese jedoch teilweise recht anschaulich interpretieren. In unserem Kontext rechtfertigt erst die exakte Lösung der Schrödingergleichung die heuristische Einführung der deBroglie-Wellenlänge.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 21. Jul 2012 05:26 Titel: jh8979 Verfasst am: 21. Jul 2012 05:26 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
..., wenn also in einem gewissen Raumbereich näherungsweise eine ebene Welle vorliegt. Für gut lokalisierte Wellenpakete im Ortsraum kann man die o.g. Rechnung zwar durchführen, die Interpretation ist jedoch wenig aussagekräftig.
|
Das ist natuerlich richtig, allerdings beraegt fuer ein Teilchen das ungefaher auf Atomgroesse lokalisiert ist  , die Breite im Impulsraum auch "nur" , die Breite im Impulsraum auch "nur"  . Fuer Teilchen mit Impulsen . Fuer Teilchen mit Impulsen 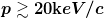 (was selbst fuer Elektronen noch nicht-relativistisch ist), laesst sich also locker eine Wellenlaenge mit weniger als 5% "Fehler" angeben. (was selbst fuer Elektronen noch nicht-relativistisch ist), laesst sich also locker eine Wellenlaenge mit weniger als 5% "Fehler" angeben. |
|
 |
winter
Anmeldungsdatum: 19.07.2012
Beiträge: 70
Wohnort: Berlin
|
 winter Verfasst am: 21. Jul 2012 11:25 Titel: winter Verfasst am: 21. Jul 2012 11:25 Titel: |
 |
|
| jh8979 hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: |
..., wenn also in einem gewissen Raumbereich näherungsweise eine ebene Welle vorliegt. Für gut lokalisierte Wellenpakete im Ortsraum kann man die o.g. Rechnung zwar durchführen, die Interpretation ist jedoch wenig aussagekräftig.
|
Das ist natuerlich richtig, allerdings beraegt fuer ein Teilchen das ungefaher auf Atomgroesse lokalisiert ist  , die Breite im Impulsraum auch "nur" , die Breite im Impulsraum auch "nur"  . Fuer Teilchen mit Impulsen . Fuer Teilchen mit Impulsen 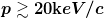 (was selbst fuer Elektronen noch nicht-relativistisch ist), laesst sich also locker eine Wellenlaenge mit weniger als 5% "Fehler" angeben. (was selbst fuer Elektronen noch nicht-relativistisch ist), laesst sich also locker eine Wellenlaenge mit weniger als 5% "Fehler" angeben. |
5 % hört sich für einen experimentellen Nachweis super an, aber bei Wellenlänge mit 5 % Unterschied läuft die berechnete und tatsächliche Welle hoffnungslos auseinander, d.h. die muss eigentlich exact sein, damit es nicht passiert.. Kohärenzlänge zwischen Theorie und Experiment.. und wir reden ja über zwei theoretische Werte, einer nach de Broglie und einer aus der Wellengleichung, und da gibt es keine Messungenauigkeiten..die sollten also gleich sein
und da sehe ich eben den Widerspruch: es gibt Quellen, wonach die De Broglie Wellenlänge mit ca. 5 % Genauigkeit nachgewiesen wurde, und wir reden davon, dass die Wellengleichung nur sehr verschwommene Ergebnisse dazu liefert...
auf Bellsche Logik will ich noch getrennt eingehen, gucke erst was Ihr schon dazu habt |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 21. Jul 2012 13:35 Titel: TomS Verfasst am: 21. Jul 2012 13:35 Titel: |
 |
|
| winter hat Folgendes geschrieben: | | ... aber bei Wellenlänge mit 5 % Unterschied läuft die berechnete und tatsächliche Welle hoffnungslos auseinander, d.h. die muss eigentlich exact sein, damit es nicht passiert.. |
1) Es gibt keine zwei theoretisch berechnete Wellenlängen, eine aus der Schrödingergleichung und eine andere gemäß deBroglie. Es gibt nur eine Wellenlänge, die aus der Schrödinbgegleichung und der Wellenfunktion folgt, und die in den o.g. Fällen mit der deBroglie-Wellenlänmge für ebene Wellen übereinstimmt. Wenn diese Übereinstimmung (aufgrund starker Lokalisierung eines Wellenpaketes, gebundenen Zuständen usw.) nicht vorliegt, dann ist die Annahme einer deBroglie-Wellenlänge einer ebenen Welle sinnlos, dann gilt einfach die Quantenmechanik.
2) Es gibt auch keine zwei verschiedenen Wellenlängen, eine berechnete aus der Schrödingergleichung und eine aus dem Experiment. Der Punkt ist, dass die Quantenmechanik in bisher allen Fällen in (bis auf experimentelle Unsicherheiten) in exakter (!) Übereinstimmung mit dem Experiment diese Wellenphänomene vorhersagt. Alles ist aus der Quantenmechanik ableitbar, die experimentellen Ergebnisse sowie der Spezialfall von deBroglie
Du solltest akzeptieren, dass die Quantenmechanik richtig ist; alles andere ist dann entweder ein Spezialfall der QM, oder - wenn im Widerspruch zur QM - dann letztlich falsch.
Ich habe mir mal den Beitrag zu Materiewellen in der Wikipedia durchgelesen. Du kannst davon ausgehen, dass diese Aussaegn für freie Teilchen und (zumindest näherungsweise) ebene Wellen korrekt sind. In diesen Fällen passt das "einfache" Bild einer festen und exakten deBroglie-Wellenlänge und es befindet sich in Übereinstimmung mit der QM. In anderen Fällen (wie gesagt: stark lokalisierte Wellenpakete, gebundene Zustände) trifft das Bild gemäß deBroglie nicht mehr zu.
http://de.wikipedia.org/wiki/Materiewelle
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 21. Jul 2012 15:55 Titel: TomS Verfasst am: 21. Jul 2012 15:55 Titel: |
 |
|
Wenn es dich interessiert, dann können wir das mal für ein konkretes Beispiel eines Wellenpaketes oder Wellenzuges ausrechnen
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 21. Jul 2012 19:19 Titel: jh8979 Verfasst am: 21. Jul 2012 19:19 Titel: |
 |
|
| winter hat Folgendes geschrieben: |
5 % hört sich für einen experimentellen Nachweis super an, aber bei Wellenlänge mit 5 % Unterschied läuft die berechnete und tatsächliche Welle hoffnungslos auseinander, d.h. die muss eigentlich exact sein, damit es nicht passiert.. Kohärenzlänge zwischen Theorie und Experiment.. und wir reden ja über zwei theoretische Werte, einer nach de Broglie und einer aus der Wellengleichung, und da gibt es keine Messungenauigkeiten..die sollten also gleich sein
und da sehe ich eben den Widerspruch: es gibt Quellen, wonach die De Broglie Wellenlänge mit ca. 5 % Genauigkeit nachgewiesen wurde, und wir reden davon, dass die Wellengleichung nur sehr verschwommene Ergebnisse dazu liefert...
|
Sorry, Ich hab mich vielleicht etwas widerspruechlich (und zu kurz) ausgedrueckt. Es ging mir nicht darum zu zeigen dass man irgendeinen 5%igen Unterschied experiementell bestimmen koennte. Wie TomS schon gesagt hat geht dies nicht.
Mir ging es lediglich darum zu zeigen, dass es auch bei lokalisierten Wellenfunktionen durchaus Sinn machen *kann* eine Wellenlaenge zu definieren... aber nicht immer muss. Das kommt dann auf das konkrete System an. |
|
 |
winter
Anmeldungsdatum: 19.07.2012
Beiträge: 70
Wohnort: Berlin
|
 winter Verfasst am: 24. Jul 2012 10:37 Titel: winter Verfasst am: 24. Jul 2012 10:37 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Wenn es dich interessiert, dann können wir das mal für ein konkretes Beispiel eines Wellenpaketes oder Wellenzuges ausrechnen |
ja, ein Elektron bewegt sich translatorisch mit V=0,8*c, es ist weit von allen Feldern, also Felder sind ausgeglichen in allen Richtungen
welche Wellenlänge der Ortswahrscheinlichkeits-Welle ergibt sich? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 24. Jul 2012 12:57 Titel: TomS Verfasst am: 24. Jul 2012 12:57 Titel: |
 |
|
| winter hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Wenn es dich interessiert, dann können wir das mal für ein konkretes Beispiel eines Wellenpaketes oder Wellenzuges ausrechnen |
ja, ein Elektron bewegt sich translatorisch mit V=0,8*c, es ist weit von allen Feldern, also Felder sind ausgeglichen in allen Richtungen
welche Wellenlänge der Ortswahrscheinlichkeits-Welle ergibt sich? |
Gegenfrage: ein Elektron als unendlich ausgedehnte ebene Welle, oder als realistisches Wellenpaket?
Für den Impuls gilt
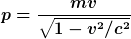
Für die deBroglie-Wellenlänge gilt:
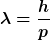
Damit kann man das berechnen. Ich komme auf ca. 1.8 Pikometer
Ich komme auf 1.8
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
winter
Anmeldungsdatum: 19.07.2012
Beiträge: 70
Wohnort: Berlin
|
 winter Verfasst am: 24. Jul 2012 13:59 Titel: winter Verfasst am: 24. Jul 2012 13:59 Titel: |
 |
|
das ist klar)
wollten Sie es nicht aus der QM-Wellengleichung?
nehmen Sie das Paket, Elektron ist äußerst wahrscheinlich nicht unendlich lang
und das Paket muss doch eine Grundfrequenz haben? |
|
 |
winter
Anmeldungsdatum: 19.07.2012
Beiträge: 70
Wohnort: Berlin
|
 winter Verfasst am: 24. Jul 2012 14:04 Titel: winter Verfasst am: 24. Jul 2012 14:04 Titel: |
 |
|
|
bzw, es ist die Wellenlänge mit der grössten Aufenthaltswahrscheinlichkeit, die Mitte der Bergspitzen |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 24. Jul 2012 17:20 Titel: TomS Verfasst am: 24. Jul 2012 17:20 Titel: |
 |
|
OK, im Falle eines Wellenpakets wird wie folgt gerechnet:
Gegeben sei ein beliebiges Wellenpaket
)
Daraus berechnet man das Wellenpaket im Impulsraum mittels Fouriertransformation
 = \int_{-\infty}^{+\infty}dx\,e^{-ipx}\,\psi(x,t))
Daraus bestimmt man den Erwartungswert des Impulses
|^2)
Damit gilt dann für die deBroglie-Wellenlänge:

Da das Wellenpaket eine gewisse Breite hat, liegt auch für den Impuls eine Unschärfe vor, d.h. dass prinzipiell auch die Wellenlänge nicht mehr scharf definiert ist.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
|

















