| Autor |
Nachricht |
NetStudent
Anmeldungsdatum: 10.07.2014
Beiträge: 6
|
 NetStudent Verfasst am: 10. Jul 2014 14:56 Titel: Dyadisches Produkt NetStudent Verfasst am: 10. Jul 2014 14:56 Titel: Dyadisches Produkt |
 |
|
Hallo,
es folgt viel Text, aber ich hoffe trotzdem, dass sich jemand findet, der mir bei dem Thema etwas weiterhelfen kann.
Ich kämpfe seit längerer Zeit mit dem Unterschied zwischen Skalarprodukt und dyadischem Produkt bei Vektoren bzw. Tensoren.
Wenn ich es richtig verstehe, beschreibt man einen Vektor v erstmal als
) . .
Dank der Regeln für Matrizenmultiplikation kann man ihn aber auch durch eine Spalten- und eine Zeilenmatrix darstellen (z. B. im 3d-Raum):
 . .
Im kartesischen Koordinatensystem mit orthonalen Basisvektoren ist das Skalarprodukt

was ich auch noch verstehe, da sich das aus der Definition des Skalarprodukts (mit cos zwischen den Vektoren) und somit auch aus der Darstellung ohne Matrizen ergibt ( ). ).
Nun beschäftige ich mich momentan mit der Tensoralgebra und lese in Skripten dazu gern mal, wie wichtig das dyadische Produkt ist, um aus vorhandenen Tensoren neue zu bilden.
Dabei stellen sich für mich mehrere Fragen:
1. Spielt das Skalarprodukt bei allgemeinen Koordinatentransformationen noch eine Rolle (abgesehen von ko- und kontravarianten Basisvektoren)?
2. Inwiefern unterscheidet sich das dyadische Produkt vom Skalarprodukt (kann man das dyadische Produkt irgendwie anhand der matrizenlosen Darstellung von v erklären?).
Laut Quelle 1, Seite 5, ist es einfach die Darstellung des allgemeinen Skalarprodukts in einer 3x3 Matrix (wenn ich das richtig verstehe).
In Quelle 2 ergibt das dyadische Produkt aber direkt einen Tensor (ohne Einheitsdyaden?).
3. Welche Rolle spielt das dyadische Produkt, um Tensoren zu bilden, bzw. warum sind die Vektoren, die im dyadischen Produkt vorkommen, auf einmal unabhängig von der Basis (soweit ich das verstanden habe, müssten die Komponenten ja von den Einheitsdyaden abhängen)?
Grüße NetStudent |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 10. Jul 2014 20:25 Titel: Jayk Verfasst am: 10. Jul 2014 20:25 Titel: |
 |
|
Die Darstellung  habe ich noch nie gesehen. Ich weiß nicht, wer sich was dabei gedacht hat, doch sie ist mit Sicherheit falsch. Spaltenvektoren sind Elemente von habe ich noch nie gesehen. Ich weiß nicht, wer sich was dabei gedacht hat, doch sie ist mit Sicherheit falsch. Spaltenvektoren sind Elemente von  mit einem Körper K. mit einem Körper K.  sind keine Körperelemente. sind keine Körperelemente.
Das Tensorprodukt zweier K-Vektorräume (oder allgemeiner zweier R-Moduln) ist selbst ein K-Vektorraum, der dadurch definiert ist, dass er die universelle Abbildungseigenschaft erfüllt: Es soll eine bilineare Abbildung  \mapsto v \otimes w) geben, sodass es für jede bilineare Abbildung geben, sodass es für jede bilineare Abbildung  eine lineare Abbildung eine lineare Abbildung  , sodass , sodass  . Konstruieren kann man das Tensorprodukt im Falle von endlich-dimensionalen Vektorräumen als direkte Summe formaler Kombinationen von Basisvektoren (es ist nämlich für Vektorräume, da sie immer eine Basis haben, . Konstruieren kann man das Tensorprodukt im Falle von endlich-dimensionalen Vektorräumen als direkte Summe formaler Kombinationen von Basisvektoren (es ist nämlich für Vektorräume, da sie immer eine Basis haben, ) , falls (vi) und (wj) Basen sind). [wenn dich die Theorie interessiert, empfehle ich einen Blick in Bosch/Algebra] , falls (vi) und (wj) Basen sind). [wenn dich die Theorie interessiert, empfehle ich einen Blick in Bosch/Algebra]
So weit zur mathematischen Präzision. Unter Physikern ist es eher üblich, unter dem Tensor  direkt eine Bilinearform zu verstehen. Das ist sinnvoll insofern, dass man jede Bilinearform als Linearkombination von Basisformen direkt eine Bilinearform zu verstehen. Das ist sinnvoll insofern, dass man jede Bilinearform als Linearkombination von Basisformen  \mapsto \delta_{i j} ) darstellen kann. Dann bezeichnet man einfach darstellen kann. Dann bezeichnet man einfach  und erhält allgemein und erhält allgemein
 \mapsto \langle x , v \rangle \langle w, y \rangle )
Wie bereits angesprochen, kann man Bilinearform als Linearkombination von Basisformen darstellen, was es ermöglicht, sie durch eine Matrix darzustellen. Bezüglich geeigneter Basen entspricht dem dann die Matrix
^t \otimes (w_1, \dots, w_n)^t = (v_1, \dots , v_n) (w_1, \dots, w_n)^t = ( v_i \cdot w_j )_{i, j})
Vielleicht ist das die einfachste, zugleich aber auch schlampigste Erklärung:

(ich bevorzuge es, das Transponiert-Zeichen rechts anzuhängen - bloß, damit es keine Verwirrung gibt, denn einige Mathematiker hängen es lieber links an)
Physikerdenkweise... Ja, Physiker sind oft nicht sehr präzise, zwischen Bilinearformen, Tensoren, Endomorphismen und Matrizen zu unterscheiden... Und sowieso ist jeder Vektor ein Spaltenvektor...
Zu den Fragen direkt:
1. weiß nicht, wie die Frage gemeint ist. Skalarprodukte sind jedenfalls sehr wichtig, denn sie ermöglichen es dir erst, überhaupt so etwas wie Orthogonalität zu definieren. Das ist ein sehr abstrakter Begriff und Orthonormalbasen sind unheimlich wichtig, spätestens in der Quantenmechanik.
2. ja, kann man. Schrei, wenn du mehr willst.
3. Kommt darauf an, was du unter einem Tensor verstehst. Gemeint ist wohl in diesem Zusammenhang, dass sie ein bestimmtes Transformationsverhalten besitzen.
EDIT: Etwas Wichtiges sollte wohl noch erwähnt werden. Als du gesagt hast, du beschäftigst dich mit der Tensoralgebra, nahm ich irgendwie an, du meintest  , denn das nennt man nunmal "die Tensoralgebra" (zusammen mit einer darauf definierten Algebrastruktur, die sich unmittelbar aus den Rechenregeln für Tensoren ergibt). Das hat die Antwort wohl etwas in die falsche Richtung gelenkt. Jedenfalls ist der Bezug zu Tensoren in der Physik (so etwas wie kovariant und kontravariant) gegeben durch die Isomorphien , denn das nennt man nunmal "die Tensoralgebra" (zusammen mit einer darauf definierten Algebrastruktur, die sich unmittelbar aus den Rechenregeln für Tensoren ergibt). Das hat die Antwort wohl etwas in die falsche Richtung gelenkt. Jedenfalls ist der Bezug zu Tensoren in der Physik (so etwas wie kovariant und kontravariant) gegeben durch die Isomorphien
 \cong V^* \otimes W, \operatorname{Bil}(V, W ; K) \cong V^* \otimes W^*) . .
Beim Tensorprodukt ist man aber eher etwas schlampig, zwischen Isomorphie und Gleichheit zu unterscheiden, daher kann man wohl ohne Weiteres auch Endomorphismen als Tensoren auffassen, denn der entsprechende Raum erfüllt die universelle Abbildungseigenschaft (man kann beweisen, dass das Tensorprodukt bis auf Isomorphie eindeutig ist). Jedenfalls kann man daran auch sehr schön den Bezug zum Transformationsverhalten sehen: Zu jeder Basis von V kann man eine duale Basis zu V* konstruieren, wobei aber der i-te Vektor der dualen Basis nicht nur von i-ten Vektor der Basis, sondern von der gesamten Basis abhängt. Du kannst ja mal konkret durchrechnen, wie sich ein "Vektor" (kontravariant) unter einem Basiswechsel verhält und was ein Dualvektor tut. Dann siehst du auch, woher die Namen ko- und kontravariant kommen. |
|
 |
NetStudent
Anmeldungsdatum: 10.07.2014
Beiträge: 6
|
 NetStudent Verfasst am: 11. Jul 2014 13:59 Titel: NetStudent Verfasst am: 11. Jul 2014 13:59 Titel: |
 |
|
Erst einmal vielen Dank für deine ausführliche Erläuterung.
Das mit der "Zeilenvektor mal Spaltenvektor"-Darstellung des Vektors hab ich aus Quelle 2 (Formel 1.3). Der Artikel hat mich aber sowieso mehr verwirrt, als er mir geholfen hat...
Ich denke, dass mir ein paar Grundlagen fehlen, da Dinge wie  \mapsto v \otimes w) für mich noch wie Hieroglyphen erscheinen. Wenn ich das richtig verstehe, wird da das Produkt zweier Vektorräume V und W (das hab ich zumindest schon öfter gelesen, verstehe aber nicht mal wie man sich das vorstellen kann) auf irgendetwas abgebildet? Kannst du mir dazu vielleicht eine Lektüre im Internet empfehlen? Solche Dinge geben mir nämlich auch einen regelmäßigen Brain-Freeze, auf Wikipedia-Artikeln mit mathematischem Hintergrund... für mich noch wie Hieroglyphen erscheinen. Wenn ich das richtig verstehe, wird da das Produkt zweier Vektorräume V und W (das hab ich zumindest schon öfter gelesen, verstehe aber nicht mal wie man sich das vorstellen kann) auf irgendetwas abgebildet? Kannst du mir dazu vielleicht eine Lektüre im Internet empfehlen? Solche Dinge geben mir nämlich auch einen regelmäßigen Brain-Freeze, auf Wikipedia-Artikeln mit mathematischem Hintergrund...
Zu deinem Angebot auf Frage 2: *schrei* |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 11. Jul 2014 15:31 Titel: Jayk Verfasst am: 11. Jul 2014 15:31 Titel: |
 |
|
Ja, ich habe mittlerweile auch mitbekommen, dass Wikibooks Schuld ist.  Man schreibt so etwas manchmal symbolisch, aber das hat eigentlich keine mathematische Bedeutung. Man schreibt so etwas manchmal symbolisch, aber das hat eigentlich keine mathematische Bedeutung.
Welchen mathematischen Hintergrund hast du? Ich habe versucht, es so zu schreiben, dass es mit linearer Algebra 1 verständlich ist (nicht ohne Grund wird das Tensorprodukt, bei uns jedenfalls, in linearer Algebra 2 behandelt).
Weißt du, was ein Vektorraum ist? Sagen wir, wir haben einen n-dimensionalen reellen Vektorraum V. Sagen wir, dieser hat eine Basis  . Dann ist dieser isomorph zum . Dann ist dieser isomorph zum  , das heißt, es gibt eine lineare eineindeutige Abbildung , das heißt, es gibt eine lineare eineindeutige Abbildung  , die eben e1 auf den Spalten(!)vektor (1,0,...) abbildet, e2 auf den Spalten(!)vektor (0,1,0,...) usw. , die eben e1 auf den Spalten(!)vektor (1,0,...) abbildet, e2 auf den Spalten(!)vektor (0,1,0,...) usw.
Dann gibt es noch den Dualraum V*. Das sind die Linearformen auf V, also lineare Abbildungen von V nach R. Dieser ist ebenfalls isomorph zum R^n (und damit auch ebenfalls n-dimensional und schließlich auch isomorph zu V) und man bekommt eine Basis, wenn man eine Basis von v hat:  := \delta_{i j}) , also zum Beispiel der erste Vektor der Dualbasis ist die Abbildung, die den ersten Basisvektor auf 1 abbildet und alle anderen auf 0. Man kann diese Vektoren ganz normal als Vektorraumhomomorphismen ansehen und sie dementsprechend auch als 1xn-Matrizen schreiben, wenn man für V e1,... als Basis wählt und für R die Eins. Deshalb identifiziert man Dualraumvektoren mit Zeilen(!)vektoren. , also zum Beispiel der erste Vektor der Dualbasis ist die Abbildung, die den ersten Basisvektor auf 1 abbildet und alle anderen auf 0. Man kann diese Vektoren ganz normal als Vektorraumhomomorphismen ansehen und sie dementsprechend auch als 1xn-Matrizen schreiben, wenn man für V e1,... als Basis wählt und für R die Eins. Deshalb identifiziert man Dualraumvektoren mit Zeilen(!)vektoren.
Wenn man nun einen Basiswechsel B->B' macht, gibt man diesen durch eine Matrix an, die Basiswechselmatrix. Diese ist die Darstellungsmatrix der identischen Abbildung bezüglich der Basen B bzw. B'. Also wenn du eine Basiswechselmatrix hast

so heißt das, dass der erste Basisvektor von B in der neuen Basis die Darstellung (1,2) (als Spalte) hat.
Rechnen wir mal: Du hast einen Basiswechsel S (deine Matrix). Dann kannst du dir überlegen (weil nämlich  , also die identische Abbildung verknüpft mit der identischen Abbildung ist immernoch die identische Abbildung, und wenn du das einmal bezüglich der Basen B, B' und einmal anders herum machst, bekommst du die Identität bezüglich B und B, also die Einheitsmatrix), dass die Umkehrung , also die identische Abbildung verknüpft mit der identischen Abbildung ist immernoch die identische Abbildung, und wenn du das einmal bezüglich der Basen B, B' und einmal anders herum machst, bekommst du die Identität bezüglich B und B, also die Einheitsmatrix), dass die Umkehrung  dir angibt, welche Darstellung der neue Basisvektor bezüglich der alten Basis hat, was nichts anderes bedeutet als dir angibt, welche Darstellung der neue Basisvektor bezüglich der alten Basis hat, was nichts anderes bedeutet als
_{i j} b_j)
(wenn die Vektoren mit bj bzw. b'i bezeichnet werden).
Wenn du einen Vektor 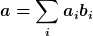 hast, bekommst du für ihn die Darstellung hast, bekommst du für ihn die Darstellung  , also sind die neuen Komponenten , also sind die neuen Komponenten  . Oder geschrieben mit Zeilenvektoren (durch Tilde gekennzeichnet) . Oder geschrieben mit Zeilenvektoren (durch Tilde gekennzeichnet)  . .
Hast du andererseits einen Dualvektor  , dann kommt der Begriff der dualen Abbildung ins Spiel: Die duale Abbildung der identischen Abbildung auf V ist die identische Abbildung auf V*. Allgemeiner: Hast du für V Basen B und B' und willst die duale Abbildung bezüglich der dualen Basen B'* und B* haben, so wird dies durch die transponierte Matrix realisiert (das bedeutet, Zeilen und Spalten müssen vertauscht werden). Also heißt das, der Basisvektor bi'* hat bezüglich der Basis B* die Darstellung der j-ten Spalte der transponierten Matrix, also der j-ten Zeile der Basiswechselmatrix. Das heißt , dann kommt der Begriff der dualen Abbildung ins Spiel: Die duale Abbildung der identischen Abbildung auf V ist die identische Abbildung auf V*. Allgemeiner: Hast du für V Basen B und B' und willst die duale Abbildung bezüglich der dualen Basen B'* und B* haben, so wird dies durch die transponierte Matrix realisiert (das bedeutet, Zeilen und Spalten müssen vertauscht werden). Also heißt das, der Basisvektor bi'* hat bezüglich der Basis B* die Darstellung der j-ten Spalte der transponierten Matrix, also der j-ten Zeile der Basiswechselmatrix. Das heißt
_{j} b^*_i) . .
Andererseits gilt genauso wieder
^{-1})_{i j} b'^*_j) . .
Somit transformiert sich der Dualvektor
^{-1})_{i j} b'^*_j)
Die neue Darstellung von alpha bezüglich der Basis B* als Spalten(!)vektor (kein Fehler, denn es geht um die Basis B*!) ist dann also

die Darstellung als Zeilenvektor (nämlich bezüglich der Basen B und der Körpereins) bekommst du durch Transponieren:
^{-1})
Wenn S einfach eine orthogonale Transformation (also zum Beispiel eine Drehung) ist, ergibt sich ein einfacherer Zusammenhang:
 . .
Kannst dir überlegen, was das komponentenweise bedeutet.
Halten wir fest: Die Koordinatendarstellungen für Vektoren aus V und Dualvektoren V* transformieren sich unterschiedlich.
Nun gibt es auch Objekte mit mehr Indizes: quadratische Matrizen können sowohl Endomorphismen als auch Bilinearformen beschreiben. Beispiel für einen Endomorphismus ist der Trägheitsoperator:  , ein Beispiel für eine Bilinearform das, was man üblicherweise als Trägheitstensor bezeichnet: , ein Beispiel für eine Bilinearform das, was man üblicherweise als Trägheitstensor bezeichnet: ) (das hier ist eigentlich eine quadratische Form, aber ob du zwei unterschiedliche Argumente einsetzt oder zweimal dasselbe, spielt keine Rolle, es geht in beide Richtungen keine Information verloren). Beide Objekte werden gewöhnlich als Trägheitstensor bezeichnet. (das hier ist eigentlich eine quadratische Form, aber ob du zwei unterschiedliche Argumente einsetzt oder zweimal dasselbe, spielt keine Rolle, es geht in beide Richtungen keine Information verloren). Beide Objekte werden gewöhnlich als Trägheitstensor bezeichnet.
[Anmerkung: Aber nichts desto trotz haben sie ein anderes Transformationsverhalten, wenn man einen nicht-orthogonalen Basiswechsel durchführt]
Ich versuche mal zu erklären, wieso. Das Tensorprodukt kommt aus der multilinearen Algebra. Hast du eine Bilinearform, so ist es egal, ob du das erste Argument verdoppelst oder das zweite, du bekommst jedenfalls denselben Wert heraus. So ergibt sich die Frage, ob es nicht möglich ist, die Bilinearform als einfach-lineare Abbildung von irgendwelchen abstrakteren Objekten zu schreiben, denn offensichtlich hast du nicht wirklich "zwei Freiheitsgrade". Diese abstrakteren Objekte sind Tensoren. Durch  wird diese neue Menge bezeichnet, die "Tensorprodukt von V und V" genannt wird (manchmal schreibt man an das Produkt noch heran, über welchem Körper man die Vektorräume auffasst, denn zum Beispiel ist jeder reeller Vektorraum auch ein rationaler, aber dann eben ein unendlichdimensionaler, über Moduln gibt es da auch ganz tolle Dinge, mit denen man uns Studenten ärgern kann). Über Vektorräumen ist die Situation wirklich recht einfach: der Vektorraum der Bilinearformen eignet sich als Tensorprodukt, denn er erfüllt genau die Eigenschaften: Der Raum der Bilinearformen auf V, V ist n²-dimensional und wenn du eine Basis B von V hast, bekommst du für ihn ebenfalls eine Basis durch die Abbildungen wird diese neue Menge bezeichnet, die "Tensorprodukt von V und V" genannt wird (manchmal schreibt man an das Produkt noch heran, über welchem Körper man die Vektorräume auffasst, denn zum Beispiel ist jeder reeller Vektorraum auch ein rationaler, aber dann eben ein unendlichdimensionaler, über Moduln gibt es da auch ganz tolle Dinge, mit denen man uns Studenten ärgern kann). Über Vektorräumen ist die Situation wirklich recht einfach: der Vektorraum der Bilinearformen eignet sich als Tensorprodukt, denn er erfüllt genau die Eigenschaften: Der Raum der Bilinearformen auf V, V ist n²-dimensional und wenn du eine Basis B von V hast, bekommst du für ihn ebenfalls eine Basis durch die Abbildungen 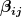 , die so definiert sind: , die so definiert sind:  = \delta_{i k} \delta_{j l}) . Fasst man den Raum der bilinearen Abbildung auf V, V als Tensorprodukt V(x)V auf, dann bezeichnet man diese neue Basis einfach mit . Fasst man den Raum der bilinearen Abbildung auf V, V als Tensorprodukt V(x)V auf, dann bezeichnet man diese neue Basis einfach mit  . .
Das ist theoretisch möglich. Allerdings hätte man vielleicht lieber eine koordinatenunabhängige Darstellung (also lieber einen kanonischen Isomorphismus). Kanonisch sind die Isomorphismen, die ich dir am Ende des letzten Beitrags geschrieben habe. Zwar ist auch  , aber der Isomorphismus ist nicht kanonisch (wie wir oben gesehen haben: das Transformationsverhalten ist ein anderes). , aber der Isomorphismus ist nicht kanonisch (wie wir oben gesehen haben: das Transformationsverhalten ist ein anderes).
Noch etwas zu den Dualvektoren: Ein Skalarprodukt kann auch dazu dienen, dass man sich nicht mit Dualvektoren auseinandersetzen muss. Du kannst nämlich jeden Dualvektor durch einen (kovarianten) Vektor ersetzen, der bei der Skalarproduktbildung das selbe macht. Jedenfalls in reellen Vektorräumen geht das (in komplexen nicht).
EDIT: Wegen Frage 2. Kommt darauf, was du mit "koordinatenunabhängig" meinst. Im Prinzip ist das, was ich gerade am Ende erwähnt habe, koordinatenunabhänig in dem Sinne, dass es eben unabhängig von Koordinaten ist, man aber eine Basis braucht, um es zu definieren. Man kann das Tensorprodukt auch ohne Koordinaten definieren, dazu schreibe ich vielleicht morgen etwas. Das ist aber nicht ganz einfach. Weißt du, was ein Quotientenvektorraum (oder Faktorraum) ist? |
|
 |
NetStudent
Anmeldungsdatum: 10.07.2014
Beiträge: 6
|
 NetStudent Verfasst am: 12. Jul 2014 16:54 Titel: NetStudent Verfasst am: 12. Jul 2014 16:54 Titel: |
 |
|
| Zitat: | | Welchen mathematischen Hintergrund hast du? Ich habe versucht, es so zu schreiben, dass es mit linearer Algebra 1 verständlich ist (nicht ohne Grund wird das Tensorprodukt, bei uns jedenfalls, in linearer Algebra 2 behandelt). |
Ich hätte natürlich von Anfang an über mein mathematisches Vorwissen schreiben sollen. Bin gerade mit der BOS fertig geworden und fange mein Studium erst im Okotber an. Da ich aber schon seit längerer Zeit versuche Tensoren zu verstehen (hauptsächlich wegen der ART) und momentan etwas mehr Zeit dafür habe, wollte ich einfach versuchen diese Fragen zu klären.
| Zitat: | | Dann gibt es noch den Dualraum V*. Das sind die Linearformen auf V, also lineare Abbildungen von V nach R. |
Ich hatte das bisher immer so verstanden, dass der Dualraum ebenfalls ein Vektorraum V* ist, dessen Basisvektoren aber jeweils senkrecht auf den beiden anderen Basisvektoren des ursprünglichen Vektorraums V stehen und man dann definiert:  . Das wäre meiner Meinung nach dasselbe gewesen wie . Das wäre meiner Meinung nach dasselbe gewesen wie  := \delta_{i j}) , da das Skalarprodukt ebenfalls bilinear und symmetrisch ist. Aber wenn ich dich richtig verstehe, dann geht das nur über dem Körper der reelen Zahlen? , da das Skalarprodukt ebenfalls bilinear und symmetrisch ist. Aber wenn ich dich richtig verstehe, dann geht das nur über dem Körper der reelen Zahlen?
| Zitat: | | Wenn man nun einen Basiswechsel B->B' macht, gibt man diesen durch eine Matrix an, die Basiswechselmatrix. |
Diese Matrix kommt zustande, da man die einzelnen Komponenten des Vektors in der neuen Basis durch die alten Komponenten ausdrücken können muss?

Dabei kommt ja dann raus, dass die Komponenten der Basis von V genau umgekehrt (also kontravariant) transformieren, wie die Basis selbst (genauso wie die Basis des dualen Vektorraums V*)?
 \cdot v_{j})
 \cdot v^{*}_{j})
| Zitat: | | Nun gibt es auch Objekte mit mehr Indizes: quadratische Matrizen können sowohl Endomorphismen als auch Bilinearformen beschreiben. Beispiel für einen Endomorphismus ist der Trägheitsoperator: ..., ein Beispiel für eine Bilinearform das, was man üblicherweise als Trägheitstensor bezeichnet: ... |
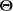 ist doch einfach ein Skalar (also eine 1x1 Matrix) und bildet somit eine Skalarmultiplikation mit ist doch einfach ein Skalar (also eine 1x1 Matrix) und bildet somit eine Skalarmultiplikation mit 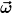 (die ja laut Definition bilinear ist)? (die ja laut Definition bilinear ist)?
Im zweiten Fall hätte man, wenn ich es richtig verstehe, ein Skalarprodukt aus zwei Vektoren, das natürlich ebenfalls bilinear und symmetrisch ist. Hier ist dann immer nur ein Vektor beteiligt, der in einer bestimmten Basis definiert ist und genauso transfomiert wie du es im letzten Beitrag geschrieben hast.
| Zitat: | | So ergibt sich die Frage, ob es nicht möglich ist, die Bilinearform als einfach-lineare Abbildung von irgendwelchen abstrakteren Objekten zu schreiben, denn offensichtlich hast du nicht wirklich "zwei Freiheitsgrade". ... |
Hier verstehe ich leider nicht ganz, was du meinst (wie man eine Bilinearform als einfach-lineare Abbildung schreiben kann). Was Moduln sind, habe ich leider nicht ganz verstanden (habe etwas im Internet gesucht), außer dass sie Verallgemeinerungen von Vektorräumen darstellen.
| Zitat: | | Der Raum der Bilinearformen auf V, V ist n²-dimensional und wenn du eine Basis B von V hast, bekommst du für ihn ebenfalls eine Basis durch die Abbildungen \beta_{i j}, die so definiert sind: \beta_{i j} (b_k, b_l ) = \delta_{i k} \delta_{j l} |
Würde das nicht nur für orthogonale Basen gelten? |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 12. Jul 2014 19:11 Titel: Jayk Verfasst am: 12. Jul 2014 19:11 Titel: |
 |
|
| NetStudent hat Folgendes geschrieben: | | Zitat: | | Welchen mathematischen Hintergrund hast du? Ich habe versucht, es so zu schreiben, dass es mit linearer Algebra 1 verständlich ist (nicht ohne Grund wird das Tensorprodukt, bei uns jedenfalls, in linearer Algebra 2 behandelt). |
Ich hätte natürlich von Anfang an über mein mathematisches Vorwissen schreiben sollen. Bin gerade mit der BOS fertig geworden und fange mein Studium erst im Okotber an. Da ich aber schon seit längerer Zeit versuche Tensoren zu verstehen (hauptsächlich wegen der ART) und momentan etwas mehr Zeit dafür habe, wollte ich einfach versuchen diese Fragen zu klären. |
Kenne ich.  Dann wünsche ich dir schon mal viel Spaß! Ich würde dir aber trotzdem empfehlen, etwas lineare Algebra zu lernen. Wenn du schnell vorankommen willst, ist Jänich empfehlenswert, den kann man im Prinzip in zwei Tagen durcharbeiten (für ein wirklich tiefes Verständnis würde ich aber Bosch empfehlen). Fischer/Lineare Algebra ist, soweit ich weiß, das einzige Buch über lineare Algebra, das das Tensorprodukt behandelt (jedenfalls für Vektorräume), und ich würde dir dazu raten, die Abschnitte dazu irgendwann durchzuarbeiten, wenn ich auch sonst den Fischer überhaupt nicht mag. Dann wünsche ich dir schon mal viel Spaß! Ich würde dir aber trotzdem empfehlen, etwas lineare Algebra zu lernen. Wenn du schnell vorankommen willst, ist Jänich empfehlenswert, den kann man im Prinzip in zwei Tagen durcharbeiten (für ein wirklich tiefes Verständnis würde ich aber Bosch empfehlen). Fischer/Lineare Algebra ist, soweit ich weiß, das einzige Buch über lineare Algebra, das das Tensorprodukt behandelt (jedenfalls für Vektorräume), und ich würde dir dazu raten, die Abschnitte dazu irgendwann durchzuarbeiten, wenn ich auch sonst den Fischer überhaupt nicht mag.
Wenn du schon etwas Vorbildung hast und nur ein paar Lücken schließen willst, ist vielleicht dieser Artikel auf dem Matheplaneten sehr gut: http://matheplanet.com/default3.html?call=article.php?sid=1420
Das würde ich probieren, bevor ich mich durch dicke Bücher schlage, denn ab Oktober wirst du das sowieso machen müssen. Vorausgesetzt, an deiner Uni hörst du lineare Algebra.
| Zitat: |
| Zitat: | | Dann gibt es noch den Dualraum V*. Das sind die Linearformen auf V, also lineare Abbildungen von V nach R. |
Ich hatte das bisher immer so verstanden, dass der Dualraum ebenfalls ein Vektorraum V* ist, dessen Basisvektoren aber jeweils senkrecht auf den beiden anderen Basisvektoren des ursprünglichen Vektorraums V stehen und man dann definiert:  . Das wäre meiner Meinung nach dasselbe gewesen wie . Das wäre meiner Meinung nach dasselbe gewesen wie  := \delta_{i j}) , da das Skalarprodukt ebenfalls bilinear und symmetrisch ist. Aber wenn ich dich richtig verstehe, dann geht das nur über dem Körper der reelen Zahlen? , da das Skalarprodukt ebenfalls bilinear und symmetrisch ist. Aber wenn ich dich richtig verstehe, dann geht das nur über dem Körper der reelen Zahlen?
|
Nein, der Dualraum existiert zu jedem Vektorraum. Ein Vektorraum ist ja etwas sehr abstraktes, eben alles, was die Vektorraumaxiome erfüllt. Zu einem Vektorraum definierst du dann die Menge der linearen Abbildungen dieses Vektorraums in den jeweiligen Grundkörper und versiehst diese mit einer Vektorraumstruktur auf naheliegende Weise: Addition, indem die Funktionswerte addiert werden (Körperaddition), skalare Multiplikation, indem die Funktionswerte multipliziert werden. Du schreibst so etwas:
 . .
Wenn du mit dem Punkt ein Skalarprodukt meinst, liegst du damit falsch. Wie gesagt, beinhaltet der Dualraum völlig andere Objekte. Es ist durchaus üblich, ähnliche Schreibweisen zu verwenden:
, \phi \in V*, v \in V) ("Paarung") ("Paarung")
 (Skalarprodukt) (Skalarprodukt)
(vom Bra-Ket-Formalismus der Quantenmechanik mal ganz zu schweigen...)
Ich weiß, in der Schule definiert man "das" Skalarprodukt über den Cosinus des Winkels. Kann man machen (finde ich auch absolut richtig), aber trotzdem ist ein Skalarprodukt etwas sehr Allgemeines, das auch theoretisch wichtig ist. Zum Beispiel in der Quantenmechanik, wo man zwischen zwei Zustandsvektoren im Hilbertraum (Raum der quadratintegrablen, komplexwertigen Funktionen) ein Skalarprodukt einführt via  \Psi (x)\,\dd^d x) . Dafür gilt ebenfalls die Cauchy-Schwartz-Ungleichung und als Ergebnis erhält man die Heisenbergsche Unschärferelation. . Dafür gilt ebenfalls die Cauchy-Schwartz-Ungleichung und als Ergebnis erhält man die Heisenbergsche Unschärferelation.
Entscheidender Punkt: Dazwischen ist kein Skalarprodukt. Für reelle Vektorräume ist das Skalarprodukt aber symmetrisch (im Gegensatz zu komplexen Vektorräumen, wo Vertauschen der Argumente eine komplexe Konjugation bewirkt), das heißt, deine Vorstellung ist gar nicht mal so falsch: Du kannst dann tatsächlich die Dualvektoren mit den Basisvektoren selbst identifizieren und als Paarung die Skalarproduktbildung nehmen. Jedenfalls, so lange du eine Orthonormalbasis hast. Diese Vorstellung wird dir aber den Blick auf das Transformationsverhalten verschleiern, da es dann diesen Effekt gar nicht gibt.
| Zitat: |
| Zitat: | | Wenn man nun einen Basiswechsel B->B' macht, gibt man diesen durch eine Matrix an, die Basiswechselmatrix. |
Diese Matrix kommt zustande, da man die einzelnen Komponenten des Vektors in der neuen Basis durch die alten Komponenten ausdrücken können muss?

Dabei kommt ja dann raus, dass die Komponenten der Basis von V genau umgekehrt (also kontravariant) transformieren, wie die Basis selbst (genauso wie die Basis des dualen Vektorraums V*)?
 \cdot v_{j})
 \cdot v^{*}_{j})
|
ja.
| Zitat: | | Zitat: | | Nun gibt es auch Objekte mit mehr Indizes: quadratische Matrizen können sowohl Endomorphismen als auch Bilinearformen beschreiben. Beispiel für einen Endomorphismus ist der Trägheitsoperator: ..., ein Beispiel für eine Bilinearform das, was man üblicherweise als Trägheitstensor bezeichnet: ... |
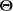 ist doch einfach ein Skalar (also eine 1x1 Matrix) und bildet somit eine Skalarmultiplikation mit ist doch einfach ein Skalar (also eine 1x1 Matrix) und bildet somit eine Skalarmultiplikation mit 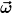 (die ja laut Definition bilinear ist)? (die ja laut Definition bilinear ist)?
Im zweiten Fall hätte man, wenn ich es richtig verstehe, ein Skalarprodukt aus zwei Vektoren, das natürlich ebenfalls bilinear und symmetrisch ist. Hier ist dann immer nur ein Vektor beteiligt, der in einer bestimmten Basis definiert ist und genauso transfomiert wie du es im letzten Beitrag geschrieben hast.
|
Nein, im Allgemeinen Fall ist das kein Skalar, dann zeigen Drehimpuls und Winkelgeschwindigkeit nicht in dieselbe Richtung. Das ist nur dann der Fall, wenn die Drehachse eine der so genannten Hauptträgheitsachsen des starren Körpers ist. Dann braucht man zur Beschreibung ein Objekt, das Vektoren in Vektoren verwandelt, nämlich einen Vektorraumendomorphismus. Diesen kann man durch eine 3x3-Matrix beschreiben. Diese ist symmetrisch (das heißt, der dazugehörige Endomorphismus ist selbstadjungiert. Dafür gibt es einen Satz, den Spektralsatz, der garantiert, dass es eine Orthonormalbasis aus Eigenvektoren gibt, es also mindestens drei Hauptträgheitsachsen gibt).
| Zitat: |
| Zitat: | | So ergibt sich die Frage, ob es nicht möglich ist, die Bilinearform als einfach-lineare Abbildung von irgendwelchen abstrakteren Objekten zu schreiben, denn offensichtlich hast du nicht wirklich "zwei Freiheitsgrade". ... |
Hier verstehe ich leider nicht ganz, was du meinst (wie man eine Bilinearform als einfach-lineare Abbildung schreiben kann). Was Moduln sind, habe ich leider nicht ganz verstanden (habe etwas im Internet gesucht), außer dass sie Verallgemeinerungen von Vektorräumen darstellen. |
Was Moduln sind, ist im Moment auch nicht wichtig, du wirst ihnen begegnen, wenn du mit linearer Algebra 2 zu tun hast (ist aber nicht überall ein Pflichtmodul, bei uns zum Beispiel nicht, und offen gesagt auch einigermaßen trocken).
Die Sache mit den Bilinearformen ist aber schon relevant. Nimm zum Beispiel folgende Form:  = v_1 w_2 - v_3 w_1) . Dann ist b(e1,e2)=1. Aber b(0.5e1,2e2) ist auch 1. Natürlich kann es sein, dass es noch weitere Kombinationen gibt, die dasselbe ergeben (so führt man dann nicht nur Tensorprodukte, sondern auch symmetrische Produkte und äußere Produkte ein, um die Besonderheiten symmetrischer bzw. alternierender Bilinearformen zu behandeln). Aber es gibt eben diese Sachen, die sich einfach aus der Bilinearität ergeben, so kann man eben schreiben . Dann ist b(e1,e2)=1. Aber b(0.5e1,2e2) ist auch 1. Natürlich kann es sein, dass es noch weitere Kombinationen gibt, die dasselbe ergeben (so führt man dann nicht nur Tensorprodukte, sondern auch symmetrische Produkte und äußere Produkte ein, um die Besonderheiten symmetrischer bzw. alternierender Bilinearformen zu behandeln). Aber es gibt eben diese Sachen, die sich einfach aus der Bilinearität ergeben, so kann man eben schreiben
 \otimes (2 \vec e_2))
und hat mit diesen Tensoren (ein allgemeiner Tensor hat dann die Form ) ) einen 9-dimensionalen Vektorraum, wo man nur noch wissen muss, auf welche Werte die Basistensoren ) einen 9-dimensionalen Vektorraum, wo man nur noch wissen muss, auf welche Werte die Basistensoren  abgebildet werden. Also man hat b auf eine Linearform reduziert. Der Terminus "Tensorprodukt" ist einfach über diese Eigenschaft definiert, dass man einen abstrakteren Vektorraum hat, mit dessen Hilfe ich multilineare Abbildungen auf lineare reduzieren kann. Wenn du einen Vektorraum findest, der das erfüllt, kannst du ihn mit Recht als Tensorprodukt bezeichnen. abgebildet werden. Also man hat b auf eine Linearform reduziert. Der Terminus "Tensorprodukt" ist einfach über diese Eigenschaft definiert, dass man einen abstrakteren Vektorraum hat, mit dessen Hilfe ich multilineare Abbildungen auf lineare reduzieren kann. Wenn du einen Vektorraum findest, der das erfüllt, kannst du ihn mit Recht als Tensorprodukt bezeichnen.
Im engeren Sinn versteht man unter Tensorprodukt eine bestimmte Konstruktion: Dann nimmt man die direkte Summe aller Paare von Vektoren
} = \lbrace \lambda_1( v, w) + \lambda_2 (x, y) + \dots \rbrace = \bigoplus_{v, w \in V} \mathbb R (v, w))
und beginnt, bestimmte Paarungen als äquivalent anzusehen, nämlich dann, wenn zu erwarten ist, dass sie zum selben Ergebnis in einer Bilinearform führen:  - (v, x) - (w, x), (lambda v, w) - \lambda (v, w) \vert v, w, x \in V) , ,  , das heißt, man betrachtet die Äquivalentklassen bezüglich der definierten Äquivalenzrelation, die man mit einer Vektorraumstruktur ausstattet. Diese Definition ist koordinatenunabhängig, aber wohl etwas übertrieben. Man benutzt sie aber, um zu zeigen, dass das Tensorprodukt stets existiert (da ein Modul im Allgemeinen keine Basis besitzt, kann man sich bei der Konstruktion also nicht darauf berufen). , das heißt, man betrachtet die Äquivalentklassen bezüglich der definierten Äquivalenzrelation, die man mit einer Vektorraumstruktur ausstattet. Diese Definition ist koordinatenunabhängig, aber wohl etwas übertrieben. Man benutzt sie aber, um zu zeigen, dass das Tensorprodukt stets existiert (da ein Modul im Allgemeinen keine Basis besitzt, kann man sich bei der Konstruktion also nicht darauf berufen).
| Zitat: |
| Zitat: | | Der Raum der Bilinearformen auf V, V ist n²-dimensional und wenn du eine Basis B von V hast, bekommst du für ihn ebenfalls eine Basis durch die Abbildungen \beta_{i j}, die so definiert sind: \beta_{i j} (b_k, b_l ) = \delta_{i k} \delta_{j l} |
Würde das nicht nur für orthogonale Basen gelten? |
[/quote]
Hier musst du deine Gedanken etwas ordnen: Ein Skalarprodukt ist eine symmetrische, positiv-definite Bilinearform. Ein reeller Vektorraum, zusammen mit einem Skalarprodukt, wird euklidischer Raum genannt. Du kannst aber auch weitere Bilinearformen betrachten. Eine Bilinearform wird dadurch festgelegt, wie sie Paare von Basisvektoren abbildet (das ermöglicht es erst, sie durch eine Matrix darzustellen). Du kannst einen euklidischen Raum betrachten, für den du keine orthogonale Basis hast, und darauf diese Formen beta_{i,j} definieren und hättest dann automatisch eine orthogonale Basis bezüglich dieser so definierten Bilinearform. Ob eine Menge von Vektoren orthogonal ist, hängt davon ab, auf welche Bilinearform man sich bezieht. Wenn man in einem euklidischen Raum ist und nichts weiter dazu sagt, meint man gewöhnlich das darauf festgelegte Skalarprodukt. |
|
 |
Vektorling
Gast
|
 Vektorling Verfasst am: 13. Jul 2014 19:40 Titel: Vektorling Verfasst am: 13. Jul 2014 19:40 Titel: |
 |
|
Also ich hab jetzt nicht alles durchgelesen aber Skalarproduct dürfte dir klar sein schätze ich. Das dyadische Produkt zwischen zwei 1-formen bedeutet z.B. :
 = \alpha(v)\beta(w))
In Komponenten  und und 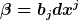
_{ij}=\alpha \otimes \beta (\partial _{i}, \partial_{j})= \alpha(\partial_{i})\beta({\partial_{j}}) = a_{i}b_{j}) (wegen multilinearität) (wegen multilinearität)
Gleiches gilt für Vektorfelder, oder mix aus Vektorfeld und formen, was dann aber linearen Transformationen entspricht.
Wenn du jetzt normale Schul Vektoren nimmst dann sieht ein Tensorprodukt so aus :
 \otimes (d,e,f) = \begin{pmatrix} a_1b_{1} & a_1b_{2} & a_1b_{3} \\ a_2b_1 & a_2b_2 & a_2b_3 \\ a_3b_1 & a_3b_2 & a_3b_3 \end{pmatrix} )
Wenn du ART lernen willst dann kannst du gleich Lineare Algebra mit den nötigen Werkzeugen lernen, guck dir mal das Buch "Linear Algebra via Exterior Products" von Sergei Winitzki an. Da fehlt dann zwar die Analysis dazu, aber das ist dann nicht mehr schwer. |
|
 |
Vektorling
Gast
|
 Vektorling Verfasst am: 13. Jul 2014 19:42 Titel: Vektorling Verfasst am: 13. Jul 2014 19:42 Titel: |
 |
|
Ohhps, ich meine das Tensorprodukt aus  
Gruß |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 13. Jul 2014 23:05 Titel: Jayk Verfasst am: 13. Jul 2014 23:05 Titel: |
 |
|
Meiner Meinung nach ist das das Tensorprodukt von  , also von einem Kovektor mit einem Vektor. , also von einem Kovektor mit einem Vektor. |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 13. Jul 2014 23:21 Titel: Jayk Verfasst am: 13. Jul 2014 23:21 Titel: |
 |
|
Ich habe im Lehrbuch der mathematischen Physik von Walter Thirring auch noch eine weniger algebraische, vielleicht für die Physik zweckmäßigere Definition gefunden.
@NetStudent: Hier geht es um Tangentialräume an Mannigfaltigkeiten. Du kannst dir einfach statt Tq(M) V vorstellen und statt Tq*(M) V*.
"Man nennt einen kontravarianten Tensor r-ter Stufe eine Abbildung
 \times \dots \times T_q^*(M) \to \mathbb R) " "
kovariant analog (eben nicht über die Dualräume). Dann wird das Tensorprodukt definiert als
 (v_1^* \dots v_r^* ; v_1 \dots v_s) = \prod_{i=1}^r v_i^*(u_i) \cdot \prod_{j=1}^s u_j^* (v_j))
Ich denke, diese Definition rechtfertigt man mit der kanonischen Isomorphie  |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 14. Jul 2014 02:27 Titel: jh8979 Verfasst am: 14. Jul 2014 02:27 Titel: |
 |
|
Du hast die Antwort nicht ernsthaft in der Nachspielzeit des WM-Finales geschrieben, oder?  |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 15. Jul 2014 19:13 Titel: Jayk Verfasst am: 15. Jul 2014 19:13 Titel: |
 |
|

Zur Rechtfertigung: Den Live-Stream auf einem Netbook zu schauen, ist auch nicht gerade der größte Genuss, so kann man schonmal abgelenkt sein.^^ |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 15. Jul 2014 23:04 Titel: jh8979 Verfasst am: 15. Jul 2014 23:04 Titel: |
 |
|
Ich geh zu Deiner Ehrenrettung einfach mal davon aus, dass Du die Antwort vorher geschrieben hast und dann in der Halbzeitpause der Verlängerung des Finales(!!) nur abgeschickt hast.... 
 |
|
 |
|
|
















 Man schreibt so etwas manchmal symbolisch, aber das hat eigentlich keine mathematische Bedeutung.
Man schreibt so etwas manchmal symbolisch, aber das hat eigentlich keine mathematische Bedeutung.


