| Autor |
Nachricht |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 04. Mai 2012 07:32 Titel: Normierungskonstante bestimmen TruEnemy Verfasst am: 04. Mai 2012 07:32 Titel: Normierungskonstante bestimmen |
 |
|
Hallo,
Meine Frage:
ich habe (zunächst) folgende Teil-Aufgabe zu lösen:
http://s14.directupload.net/images/120501/iltt78ci.png
Meine Idee:
Ich habe zunächst das Betrags-Quadrat der Wellen-
funktion ausgerechnet: da der komplexe Anteil gleich
0 ist, kann ich sie einfach quadrieren. Ich bin mir
aber nicht sicher, ob der Ausdruck so richtig ist:
http://s14.directupload.net/images/120503/xxqrftjt.jpg
Ich wüsste nicht, wie ich ihn weiter auflösen kann?
Nun habe ich das Integral über den gesamten Raum
vom erhaltenen Ausdruck ausgerechnet (was ich später
gleich 1 setzen werde, um 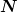 bestimmen zu können): bestimmen zu können):
zunächst splittete ich das Integral, klammerte etwas aus,
definierte mir die Exponenten gemäß dem Foto:
http://s14.directupload.net/images/120503/jbojerdy.jpg
Nun bereiten mir die Ableitungen der Betas Probleme -
' bedeutet in diesem Zusammenhang Ableitung nach x.
Über das 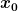 wird in der Aufgabe nichts gesagt, wird in der Aufgabe nichts gesagt,
ich nehme daher an, dass ich es einfach wie eine
Konstante zu behandeln habe, richtig? Hilfe wäre toll![/b] |
|
 |
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
 pressure Verfasst am: 04. Mai 2012 08:57 Titel: pressure Verfasst am: 04. Mai 2012 08:57 Titel: |
 |
|
|
Du hast richtig quadriert (wo bei du den Exponenten im mittleren Term noch zusammenfassen kannst), allerdings sind die Integrale falsch ausgewertet. Das Integral und damit die Größe N kann nicht mehr von x abhängig sein und ist daher eine Zahl/Konstante. Die drei Integral die du lösen musst sind Gaußintegrale (http://en.wikipedia.org/wiki/Gaussian_integral). |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 04. Mai 2012 09:35 Titel: TomS Verfasst am: 04. Mai 2012 09:35 Titel: |
 |
|
schau mal hier: http://integrals.wolfram.com/index.jsp
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 04. Mai 2012 12:31 Titel: TruEnemy Verfasst am: 04. Mai 2012 12:31 Titel: |
 |
|
Hallo,
| pressure hat Folgendes geschrieben: | | ... den Exponenten zusammenfassen ... |
Gestatte mir die Frage: Wie?
| Zitat: | | Das Integral ... ist ... eine Zahl. |
OK, hört sich soweit logisch an.
Das hätte ich berücksichtigen
müssen, sry. Aber irre ich denn
wirklich, wenn ich den letzten
Ausdruck (Foto/Link 2) hinschreibe?
Stimmt es denn nicht, dass die Stamm
-Ftk. einer e-Ftk. gegeben ist durch
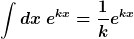
? Wo liegt der Denkfehler??
| Zitat: | | Die drei Integrale ... sind Gaußintegrale. |
Danke. Nun weiß ich also , dass
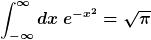
ist. Das bedeutet wohl, dass meine
von 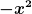 verschiedenen Expo- verschiedenen Expo-
nenten einfach ein entsprechend
anderes Ergebnis mit 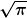 liefern. liefern.
Nur muss ich das noch nachschauen -.- |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 04. Mai 2012 13:57 Titel: TomS Verfasst am: 04. Mai 2012 13:57 Titel: |
 |
|
Der Trick zur Auswertung gaußscher Exponenten ist immer der selbe:
- quadratische Ergänzen und binomische Formel im Exponenten anwenden
- den Exponenten geeignet reskalieren und verschieben, also eine Variablentransformation
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 04. Mai 2012 15:52 Titel: TruEnemy Verfasst am: 04. Mai 2012 15:52 Titel: |
 |
|
Hallo,
vielen Dank. Das habe ich soeben gemacht.
Aber leider kommt schon bei der quadratischen
Ergänzung irgendwie totaler Mist raus 
Gruß.
EDIT:
Könnte folgende die Lösung sein, zumindest
für den Exponent des ersten Gauß-Integrals?
^2} = \sqrt{\frac{\pi}{\alpha}}\;,\;\alpha > 0$) |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
|
 |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 04. Mai 2012 23:15 Titel: TruEnemy Verfasst am: 04. Mai 2012 23:15 Titel: |
 |
|
Hallo,
das erste Integral stimmt also?
Dann wird das zweite wohl lauten:
^2} = \sqrt{\frac{\pi}{\alpha}}\;,\;\alpha > 0$)
Nun kommt das 'schwerste' dran.
In wie weit kann ich den Exponenten
da noch vereinfachen? Iwie bin ich
diesbezüglich zur Zeit blind ... sehe
es nicht, auch nach längerem Grübeln. |
|
 |
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
 pressure Verfasst am: 05. Mai 2012 09:12 Titel: pressure Verfasst am: 05. Mai 2012 09:12 Titel: |
 |
|
Das ist überhaupt nicht das schwerste, eher sogar einfacher, wenn man ein bisschen umformt:
^2+(x-x_0)^2\bigr)\right]\,\dx=\int\exp\left[-\alpha \left(x^2+x_0^2\right)\right]\,\dx=\exp(-\alpha x_0^2)\int \exp(-\alpha x^2)\,\dx)
Kommst du nun drauf? |
|
 |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 05. Mai 2012 13:40 Titel: TruEnemy Verfasst am: 05. Mai 2012 13:40 Titel: |
 |
|
Hallo,
und Danke! Schwerer als die anderen beiden, finde ich, ist es schon, denn:
ich habe die Umformbarkeit des Exponenten eben nicht erkannt, leider!
^2 + \left(x - x_{0}\right)^2\right) = -\alpha \left(x^2 + x_{0}^2\right)$ )
Was war da nun der Trick dabei? Das Integral müssten dann also lauten:
^2 + (x + x_{0})^2)} = e^{-\alpha x_{0}^2} \; \sqrt{\frac{\pi}{\alpha}}\;\text{mit}\;e^{-\alpha x_{0}^2}\;\text{und}\;\alpha > 0 )
Zuletzt bearbeitet von TruEnemy am 05. Mai 2012 22:49, insgesamt einmal bearbeitet |
|
 |
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
 pressure Verfasst am: 05. Mai 2012 18:03 Titel: pressure Verfasst am: 05. Mai 2012 18:03 Titel: |
 |
|
Einverstanden  |
|
 |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 05. Mai 2012 23:38 Titel: TruEnemy Verfasst am: 05. Mai 2012 23:38 Titel: |
 |
|
  Dann haben wir nun folgendes: Dann haben wir nun folgendes:
|^2 = N^2 \left(\sqrt{\frac{\pi}{\alpha}} + 2\;e^{-\alpha x_{0}}\;\sqrt{\frac{\pi}{\alpha}} + \sqrt{\frac{\pi}{\alpha}}\right) = 1$ )
Woraus sich äquivalent das hier ergibt:
\right)\right)^{-\frac{1}{2}} = \left(\sqrt{\frac{4\pi}{\alpha}}\left(1 + e^{-\alpha x_{0}}\right)\right)^{-\frac{1}{2}}
<br />
$ )
Wenn ich nun den Erwartungswert
|^2$ )
berechnen will, erhalte ich folglich:
\right)^{-\frac{1}{2}} \left( \sqrt{\frac{4\pi}{\alpha}}\left(1 + e^{-\alpha x_{0}} \right) \right) \right\}$ )
\right)^{\frac{1}{2}} \right\} \left[\frac{1}{2}\;x^2\right]$ )
Zuletzt bearbeitet von TruEnemy am 06. Mai 2012 12:28, insgesamt einmal bearbeitet |
|
 |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 06. Mai 2012 12:25 Titel: TruEnemy Verfasst am: 06. Mai 2012 12:25 Titel: |
 |
|
|
Sorry, sollte ich dazu einen neuen Thread eröffnen? |
|
 |
Friedi
Anmeldungsdatum: 06.05.2012
Beiträge: 30
|
 Friedi Verfasst am: 06. Mai 2012 17:02 Titel: Friedi Verfasst am: 06. Mai 2012 17:02 Titel: |
 |
|
Bei mir kommt für den Erwartungswert 0 raus. Kann mir jemand sagen, ob das Sinn macht?
Man rechnet doch
|^2=\int dx \ x N^2 (exp[-\alpha(x+x_0)^2]+2exp[-\alpha x^2-\alpha x_0^2]+exp[-\alpha(x-x_0)^2])
<br />
)
^2]+2N^2exp[-\alpha x_0^2]\int dx \ x exp[-\alpha x^2]+N^2\int dx \ x exp[-\alpha (x-x_0)^2]=0
<br />
)
da die drei Integrale nach Gauß da
 |
|
 |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 06. Mai 2012 17:07 Titel: TruEnemy Verfasst am: 06. Mai 2012 17:07 Titel: |
 |
|
Wie kommst du darauf, dass
^2} = 0$ )
? Wir hatten doch raus, dass
^2} = \sqrt{\frac{\pi}{\alpha}}$ )
Für das Betrags-Quadrat der WF galt:
|^2 = \left(\sqrt{\frac{4\pi}{\alpha}}\left(1 + e^{-\alpha x_{0}}\right)\right)^{-\frac{1}{2}} \left( \sqrt{\frac{4\pi}{\alpha}}\left(1 + e^{-\alpha x_{0}} \right) \right) = \left(\sqrt{\frac{4\pi}{\alpha}}\left(1 + e^{-\alpha x_{0}}\right)\right)^{\frac{1}{2}} $ )
1. Klammer: Normierungskonstante,
2. Klammer: Zusammengefasste,
ausgewertete Gauß-Integrale
Zuletzt bearbeitet von TruEnemy am 06. Mai 2012 17:13, insgesamt einmal bearbeitet |
|
 |
Friedi
Anmeldungsdatum: 06.05.2012
Beiträge: 30
|
 Friedi Verfasst am: 06. Mai 2012 17:12 Titel: Friedi Verfasst am: 06. Mai 2012 17:12 Titel: |
 |
|
ja es ist

Aber wenn man den Erwartungswert ausrechnet muss man ja
|^2
<br />
)
ausrechen und das führt dann, soweit ich das richtig gerechnet habe, zu drei Integralen der Form

und das ist 0 (man beachte das x!)
Zuletzt bearbeitet von Friedi am 06. Mai 2012 17:24, insgesamt 2-mal bearbeitet |
|
 |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 06. Mai 2012 17:21 Titel: TruEnemy Verfasst am: 06. Mai 2012 17:21 Titel: |
 |
|
Ich habe halt einfach das Betrags-Quadrat der WF mit eingesetzter
Normierungskonstante in die Formel des Erwartungswertes eingesetzt.
Das Betrags-Quadrat war ja im weitesten Sinne nur eine Konstante,
welche ich aus dem Integral rausziehen kann und somit wäre geblieben:
|^2 \int dx\;x = |\psi(x,0)|^2 \left[\frac{1}{2} x^2 \right]$ )
Meine Überlegung kann aber selbstverständlich auch totaler Käse sein ... |
|
 |
Friedi
Anmeldungsdatum: 06.05.2012
Beiträge: 30
|
 Friedi Verfasst am: 06. Mai 2012 17:29 Titel: Friedi Verfasst am: 06. Mai 2012 17:29 Titel: |
 |
|
Aber  ) hängt doch immernoch von x ab, da kannst du es doch nicht einfach aus dem integral rausziehen?!? oder übersehe ich da grad was? hängt doch immernoch von x ab, da kannst du es doch nicht einfach aus dem integral rausziehen?!? oder übersehe ich da grad was? |
|
 |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 06. Mai 2012 17:31 Titel: TruEnemy Verfasst am: 06. Mai 2012 17:31 Titel: |
 |
|
Ich ziehe ja nicht $ ) aus dem Integral, sondern das Betrags-Quadrat aus dem Integral, sondern das Betrags-Quadrat |^2$ ) . .
Und das hängt offensichtlich nicht mehr vom x ab, sondern nur von 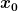 und und 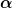 , sind aber , sind aber
beides nur Konstanten. Das kann aber, wie gesagt, totaler Blödsinn sein, ich warte auf
eine Antwort von den etwas bewandteren Usern  |
|
 |
Friedi
Anmeldungsdatum: 06.05.2012
Beiträge: 30
|
 Friedi Verfasst am: 06. Mai 2012 17:52 Titel: Friedi Verfasst am: 06. Mai 2012 17:52 Titel: |
 |
|
Nun
|^2=[N\{exp[-\alpha(x+x_0)^2/2]+exp[-\alpha(x-x_0)^2/2]\}]^2
<br />
)
^2]+2exp[-\alpha x^2 - \alpha x^2_0]+exp[-\alpha(x-x_0)^2]\}
<br />
)
wenn man auf das nun
|^2
<br />
)
anwendet, kommt aber bei mir nicht raus, dass man da irgendwie was rausziehen kann. jedenfalls nicht mehr als N^2, und auf keine fall |^2) was ich nicht ausschreiben will. was ich nicht ausschreiben will.
weiter geht die rechnung bei meinem ersten beitrag... ich weiß nicht, wo ich den fehler mache... kannst du mir helfen? |
|
 |
Friedi
Anmeldungsdatum: 06.05.2012
Beiträge: 30
|
 Friedi Verfasst am: 06. Mai 2012 17:55 Titel: Friedi Verfasst am: 06. Mai 2012 17:55 Titel: |
 |
|
|
nunja ich hoffe auch, dass sich bald einer mit ein wenig mehr ahnung noch melden wird ... |
|
 |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 06. Mai 2012 17:58 Titel: TruEnemy Verfasst am: 06. Mai 2012 17:58 Titel: |
 |
|
Sry, ich habe das Ergebnis von |^2$ ) mit dem von mit dem von |^2$ ) verwechselt. verwechselt.
Ich schaue es mir nun noch mal genauer an, aber es sieht wohl so aus, als dass du recht hast ... |
|
 |
Friedi
Anmeldungsdatum: 06.05.2012
Beiträge: 30
|
 Friedi Verfasst am: 06. Mai 2012 18:02 Titel: Friedi Verfasst am: 06. Mai 2012 18:02 Titel: |
 |
|
|
ok... wie weit bist du denn sonst so mit dem übungsblatt? |
|
 |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 06. Mai 2012 18:06 Titel: TruEnemy Verfasst am: 06. Mai 2012 18:06 Titel: |
 |
|
 Nicht sehr weit, bisher nur das, was hier besprochen wurde :/ Nicht sehr weit, bisher nur das, was hier besprochen wurde :/
Aber wenn ich nun noch die Varianz und die Fourier-Transf. hinbekomme,
habe ich schon mal mehr als 50%  |
|
 |
Friedi
Anmeldungsdatum: 06.05.2012
Beiträge: 30
|
 Friedi Verfasst am: 06. Mai 2012 18:51 Titel: Friedi Verfasst am: 06. Mai 2012 18:51 Titel: |
 |
|
also bei mir kommt
|^2=\frac{1}{2\alpha} )
raus. kannst du das oder jemand anders bestätigen?
Die Varianz ist dann
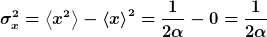 |
|
 |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 06. Mai 2012 19:17 Titel: TruEnemy Verfasst am: 06. Mai 2012 19:17 Titel: |
 |
|
Ich muss erst nochmal nachhaken,sry: Woher hast du, dass
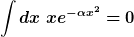 |
|
 |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 06. Mai 2012 19:35 Titel: TruEnemy Verfasst am: 06. Mai 2012 19:35 Titel: |
 |
|
Also ich habe für die Varianz was anderes raus:
Zentral dabei ist ja die Berechnung des Ausdrucks:
|^2$ )
Nach viel BlaBla sucht man die Lösung für:
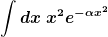 bzw. bzw. ^2}$ )
Laut dieser Liste: http://en.wikipedia.org/wiki/List_of_integrals_of_exponential_functions
ist das dann 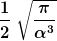 und somit komme ich auf: und somit komme ich auf:
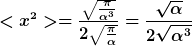
Zuletzt bearbeitet von TruEnemy am 06. Mai 2012 19:39, insgesamt einmal bearbeitet |
|
 |
Friedi
Anmeldungsdatum: 06.05.2012
Beiträge: 30
|
 Friedi Verfasst am: 06. Mai 2012 19:36 Titel: Friedi Verfasst am: 06. Mai 2012 19:36 Titel: |
 |
|
=\left[-\frac{exp(-x^2)}{2} (+const)\right]_{\mathbb R}=0
<br />
)
ist ja auch punktsymmetrisch im ursprung |
|
 |
Friedi
Anmeldungsdatum: 06.05.2012
Beiträge: 30
|
 Friedi Verfasst am: 06. Mai 2012 19:42 Titel: Friedi Verfasst am: 06. Mai 2012 19:42 Titel: |
 |
|
das ist ja gerade
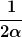
... |
|
 |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 06. Mai 2012 20:05 Titel: TruEnemy Verfasst am: 06. Mai 2012 20:05 Titel: |
 |
|
Ja, stimmt, war wieder zu voreilig und unbedacht  
Bist du schon bei der Fourier-Transformation? |
|
 |
Friedi
Anmeldungsdatum: 06.05.2012
Beiträge: 30
|
 Friedi Verfasst am: 06. Mai 2012 21:06 Titel: Friedi Verfasst am: 06. Mai 2012 21:06 Titel: |
 |
|
hmm hab grad erstmal futter gefasst  jetzt mal schauen wegen der fouriertransformierten. hast du schon was? und hast den rechenweg für die ersten zwei momente rausbekommen? ich kanns auch noch posten wenn magst. jetzt mal schauen wegen der fouriertransformierten. hast du schon was? und hast den rechenweg für die ersten zwei momente rausbekommen? ich kanns auch noch posten wenn magst. |
|
 |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 06. Mai 2012 21:21 Titel: TruEnemy Verfasst am: 06. Mai 2012 21:21 Titel: |
 |
|
Hoffe, es mundete  Ich hab bisher nur die Formel aufgeschrieben, Ich hab bisher nur die Formel aufgeschrieben,
und alles eingesetzt, bisschen umgeformt, sonst nichts.
Den Rechenweg für die Momente habe ich bereits, vielen Dank 
Ich denke, du meinst damit 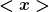 und und 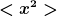 bzw. bzw. 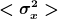 . . |
|
 |
Friedi
Anmeldungsdatum: 06.05.2012
Beiträge: 30
|
 Friedi Verfasst am: 06. Mai 2012 21:38 Titel: Friedi Verfasst am: 06. Mai 2012 21:38 Titel: |
 |
|
ja genau das meinte ich mit die momente...
^2}{2}-ikx\right]+\int dx \ exp\left[-\frac{\alpha(x-x_0)^2}{2}-ikx\right]\right]
<br />
)
würde gerne das aus der vorlesung nehmen, aber blicks grad nicht. das war

oder kann man den exponenten irgendwie jeweils gewinnbringend umformen? |
|
 |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
 TruEnemy Verfasst am: 06. Mai 2012 21:47 Titel: TruEnemy Verfasst am: 06. Mai 2012 21:47 Titel: |
 |
|
HaHa, genau an selbiger Stelle bin ich auch und am Grübeln 
Vll kann einer helfen?? Bestimmt ist dem so, nur wie, seh's grad nicht. |
|
 |
TruEnemy
Anmeldungsdatum: 01.11.2010
Beiträge: 516
|
|
 |
|



















 Dann haben wir nun folgendes:
Dann haben wir nun folgendes:

 Nicht sehr weit, bisher nur das, was hier besprochen wurde :/
Nicht sehr weit, bisher nur das, was hier besprochen wurde :/
 jetzt mal schauen wegen der fouriertransformierten. hast du schon was? und hast den rechenweg für die ersten zwei momente rausbekommen? ich kanns auch noch posten wenn magst.
jetzt mal schauen wegen der fouriertransformierten. hast du schon was? und hast den rechenweg für die ersten zwei momente rausbekommen? ich kanns auch noch posten wenn magst.