| Autor |
Nachricht |
Dude
Gast
|
 Dude Verfasst am: 31. Okt 2009 09:22 Titel: Fouriertransformation einer Poissongleichung |
 |
|
Hallo zusammen!
Ich möchte folgende Gleichung Fouriertransformieren:
 = -4 \pi \delta(\vec{r}-\vec{r_{0}}))
zur linken Seite der Gl.:
in meinem Skript steht, dass die FT von  ist, und analog dann  \phi )
Wie kommt man da drauf? Wenn ich versuche diese FT auszuführen krieg ich alles nur nicht sowas raus 
Dann zur rechten Seite:
das Integral  \, dr) ist doch per Definitionem der Deltafunktion einfach  ?
Nur wie führe ich dann die inverse Fouriertransformation aus, um die Poissongleichung schlussendlich auch lösen zu können?
|
|
 |
schnudl
Moderator
Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
| schnudl Verfasst am: 31. Okt 2009 10:08 Titel: Re: Fouriertransformation einer Poissongleichung |
|
|
| Dude hat Folgendes geschrieben: |
in meinem Skript steht, dass die FT von ist, und analog dann
Wie kommt man da drauf? |
Hast du schon versucht, mal partiell zu integrieren?
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
|
Dude
Gast
|
| Dude Verfasst am: 31. Okt 2009 10:24 Titel: Re: Fouriertransformation einer Poissongleichung |
|
|
| schnudl hat Folgendes geschrieben: |
Hast du schon versucht, mal partiell zu integrieren? |
Ja, da komme ich auf
 )
D.h. irgendwie müsste der erste Term wegfallen. Aber wieso sollte er?
|
|
|
Dude
Gast
|
| Dude Verfasst am: 31. Okt 2009 10:27 Titel: Re: Fouriertransformation einer Poissongleichung |
|
|
Das bezieht sich jetzt natürlich auf  und eine Dimension...
|
|
|
schnudl
Moderator
Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
| schnudl Verfasst am: 31. Okt 2009 10:55 Titel: Re: Fouriertransformation einer Poissongleichung |
|
|
| Dude hat Folgendes geschrieben: |
D.h. irgendwie müsste der erste Term wegfallen. Aber wieso sollte er? |
weil aus physikalischen Gründen irgendweche Felder weit weg von ihren Quellen verschwinden müssen. Ansonsten hättest du einen Fluss durch die im Unendlichen begrenzte Randfläche.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
|
Dude
Anmeldungsdatum: 31.10.2009
Beiträge: 6
|
| Dude Verfasst am: 31. Okt 2009 11:09 Titel: |
|
|
Mh.... finde ich nicht so recht überzeugend.... Das Ganze soll sich schließlich auf eine beliebige Funktion beziehen. Phi hab ich hier nur zufällig verwendet, das soll kein Potential oder sowas sein.
Aber gut, das Problem verschiebe ich gedanklich mal auf später.
Wie sieht es mit der rechten Seite der Gleichung aus? Hab ich da richtig gedacht, oder irgendeinen Fehler gemacht?
|
|
|
schnudl
Moderator
Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
| schnudl Verfasst am: 31. Okt 2009 11:48 Titel: |
|
|
zu 1)
wenn du die partielle Integration durchführst (und das ist ja erlaubt), so muss das Feld selbst oder das Integral im Unendlichen verschwinden, wenn du deine Identität voraussetzt.
Es ist eine sehr sehr gängige Methode, partiell zu integrieren und den Rand zu vernachlässigen, da er Null ist.
Zu 2)
müsste stimmen!
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
| TomS Verfasst am: 31. Okt 2009 13:33 Titel: |
|
|
Die Fouriertransformation selbst darf man auch nicht "einfach so" durchführen, sondern man muss sich sehr genau überlegen, für welche Funktionen sie überhaupt definiert ist.
Dazu betrachet man in der Funktionalanalysis sogenannte Funktionenräume, z.B. Hilberträume, die geeignet definierte Funktionen beinhalten. Ohne auf die Detailseinzugehen sei dabei der Raum der quadratintegrierbaren Funktionen hervorgehoben, denn dafür hat die Fouriertransformation besonders interessante Eigenschaften.
Der Raum ist definiert als Raum der komplexwertigen Funktionen f(x), für die das Integral
|^2 < \infty)
existiert.
Damit muss jede Funktion automatisch im Unendlichen "geeignet" gegen Null konvergieren, ansonsten ist das Integral nicht definiert.
Für diesen Raum ist die Fouriertransformation
 = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{+\infty} dx e^{-ikx} f(x))
Ein sogenannter unitärer Operator, d.h. eine unendlichdimensionale Verallgemeinerung einer komplexen Drehung. Die inverse Fouriertransformation ist auf dem selben Raum definiert, d.h. es gelten die selben Bedingungen für die Funktionen.
Dieser Raum reicht jedoch icht aus, um die Poissongleichung zu diskutieren. Man sieht dies daran, dass die Deltafunktion nicht zu diesem Raum gehört, da das Integral
|^2)
schlichtweg nicht existiert. Allerdings kann man den sogenannten Abschluss dieses Raumes definieren (anschaulich ist der Abschluss einer Menge die Menge selbst plus ihr Rand, also der Abchluss von ]0,1[ist [0,1]); die Deltafunktion gehört dann zu diesem Abschluss. Dies führt zu sogenannten temperierten Distributionen und Sobolevräumen.
In diesen Funktionenräumen (die die Basis für viele mathematische Probleme der theoretischen Physik bilden) sind die Tricks der Physiker tatsächlich erlaubt = mathematisch wohldefiniert, d.h.
- Deltafunktion und ebene Welle sind Elemente (des Abschlusses) der Räume
- die Deltafunktion ist die Ableitung einer Stufenfunktion
- die Deltafunktion ist Fouriertransformierte der ebenen Welle
- Fouriertransformationen sowie ihre Inverse sind wohldefiniert
- die Randterme verschwinden
- k-Integration und x-Ableitung sind vertauschbar
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Dude
Anmeldungsdatum: 31.10.2009
Beiträge: 6
|
| Dude Verfasst am: 31. Okt 2009 16:18 Titel: |
|
|
@TomS: Danke für die ausführliche Erklärung, damit ist mir jetzt alles klar! 
Trotzdem schaffe ich es immer noch nicht, die Poissongleichung durch FT zu lösen. Vielleicht sieht ja jemand den Fehler in meiner Rechnung:
 = -4 \pi \delta(\vec{r}-\vec{r_{0}}) )
Wie läuft die FT jetzt bei Vektoren? Komponentenweise?
Jedenfalls hab ich das ganze jetzt erst mal für eine Dimension versucht:
 = \int^{\infty}_{-\infty}e^{-ikr}\delta(r-r_{0}) \, dr = e^{-ikr_{0}} )
->
 = \frac{e^{-ikr_{0}}}{k^{2}} )
-> Rücktransformation:
 = \int^{\infty}_{-\infty} \Phi(k) e^{ikt} \, dk= \int^{\infty}_{-\infty} \frac{e^{-ikr_{0}}}{k^{2}} e^{ikt} \, dk )
Und dieses letzte Integral ist afaik nicht analytisch machbar
|
|
|
schnudl
Moderator
Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
| schnudl Verfasst am: 31. Okt 2009 16:38 Titel: |
|
|
hast du schon den Residuensatz probiert?
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
|
Dude
Anmeldungsdatum: 31.10.2009
Beiträge: 6
|
| Dude Verfasst am: 31. Okt 2009 16:44 Titel: |
|
|
| schnudl hat Folgendes geschrieben: | | hast du schon den Residuensatz probiert? |
Nein, der wäre mir neu.
Ich hab nur nach einigen erfolglosen Versuchen in einer Integraltabelle nachgesehen, und herausgefunden, dass (1/x^2)e^x keine Stammfunktion hat
|
|
|
schnudl
Moderator
Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
| schnudl Verfasst am: 31. Okt 2009 17:18 Titel: |
|
|
Zunächst kannst du ja zumindest 1x partiell integrieren und es sieht mal einfacher aus...
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
| TomS Verfasst am: 31. Okt 2009 19:26 Titel: |
|
|
Ohne Residuensatz geht es nicht
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
schnudl
Moderator
Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
| schnudl Verfasst am: 31. Okt 2009 22:11 Titel: |
|
|
Es geht zwar nicht ohne, jedoch findet man nach der partiellen Integration das Fourier-Transformierte Paar für F(k) = 1/k in den üblichen Korrespondenz-Tabellen. 
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
| TomS Verfasst am: 01. Nov 2009 01:17 Titel: |
|
|
Übrigens ist das ein interessanter Punkt, wenn man die Theorie in weniger oder mehr als drei Dimensionen betrachtet. Aufgrund des Laplaceoperators erhält man im Impulsraum immer k²; d.h. das Potential ergibt sich immer aus der Fouriertransformierten von 1/k². Da dieses Integral wie folgt von der Dimension abhängt
erhält man das Coulombpotential in D Dimensionen, speziell:
1d: lineares Potentialk ~x
2d: logarithmisches Potential
3d: 1/r Potential
4d und höher: 1/r², 1/r³, ...
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
schnudl
Moderator
Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
| schnudl Verfasst am: 01. Nov 2009 09:26 Titel: |
|
|
die ursprüngliche Frage bezog sich denke ich auf 3 Dimensionen. Wir sind aber schon etwas davon abgekommen...
= \int \frac{e^{i\vec k \vec r}}{k^2} \, d^3k )
(Ich setze die Ladung jetzt mal in den Ursprung, da es nichts am Prinzip ändert)
Das kann man in Polarkordinaten anschreiben, gemäss
= \int_k \int_\theta \frac{e^{i kr \cos \theta}}{k^2} \, 2\pi k^2 \sin \theta \, \dd \theta \dd k )
und die Integration über den Winkel explizit ausführen. Es verbleibt dann ein Integral über k, da die Winkelabhängigkeit herausfällt (muss ja so sein, da wir uns letztendlich ein Coulombpotenzial erwarten). Das überlasse ich aber dem Urheber des Threads...
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
|
Dude
Anmeldungsdatum: 31.10.2009
Beiträge: 6
|
| Dude Verfasst am: 02. Nov 2009 13:06 Titel: |
|
|
Also ich hab mich jetzt mal etwas mit dem Residuensatz beschäftigt, und frage mich jetzt: wie kann ich den hier anwenden? Eine Polstelle der Funktion liegt ja bei 0, und somit auf der reellen Achse. Das ist aber wohl nicht erlaubt? Was tun?
[Edit]
Andererseits: wenn ich diese kleine Ungereimtheit einfach mal übersehe, kommt z.B. für den eindimensionalen Fall etwas plausibles raus:
= \frac{1}{2 \pi} \int^{\infty}_{-\infty} \frac{e^{i k r}}{k^2} \, dk )
mit
= lim_{z \rightarrow 0} \frac{\partial}{\partial k}((k^2 \cdot f(k)) = i(r-r_{0}))
kriege ich dann  = (r-r_{0}) ) raus. Sieht doch ganz gut aus, und stimmt mit dem überein, was TomS geschrieben hat?
Die (wirklich letzte  ) Frage wäre dann, wie übertrage ich das auf den 3-dim. Fall?
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
| TomS Verfasst am: 02. Nov 2009 13:40 Titel: |
|
|
Ne, passt leider auch im eindimensionalen Fall nicht. Das lineare Potential entspricht der Betragsfunktion
 = \text{const.} \cdot |x - x_0|)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
| TomS Verfasst am: 02. Nov 2009 13:42 Titel: |
|
|
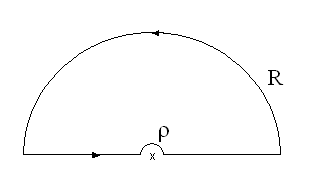
Um den Residuensatz enwenden zu können, musst du die Singularität etwas von der reellen Achse "wegschieben" und anschließend den Weg ds Integrals mit einem Halbkreis schließen; dabei wird so geschlossen, dass die komplexe e-Funktion im imaginär-unendlich verschwindet, so dass das Integral entlang des Halbkreises keinen Beitrag liefert.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Dude
Anmeldungsdatum: 31.10.2009
Beiträge: 6
|
| Dude Verfasst am: 02. Nov 2009 13:43 Titel: |
|
|
|
Mist, hast recht. Warum muss Physik so frustrierend sein? -.-
|
|
|
schnudl
Moderator
Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
|
|
Dude
Anmeldungsdatum: 31.10.2009
Beiträge: 6
|
| Dude Verfasst am: 05. Nov 2009 11:52 Titel: |
|
|
Okay, habs hingekriegt. Danke! 
|
|
|
|
Registrieren
Login
FAQ
Suchen
