| Autor |
Nachricht |
wishmoep
Anmeldungsdatum: 07.09.2008
Beiträge: 1342
Wohnort: Düren, NRW
|
 wishmoep Verfasst am: 15. Okt 2008 15:36 Titel: E-Feld eines zylindrischen Drahtes wishmoep Verfasst am: 15. Okt 2008 15:36 Titel: E-Feld eines zylindrischen Drahtes |
 |
|
Hey Leute, noch einmal eine Frage bzgl. folgender Aufgabe34.
Gegeben ist die Aufgabe | Zitat: | *4: Auf einem geradlinigen dünnen Drath der Länge 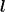 sei die Ladung sei die Ladung 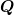 gleichmäßig verteilt. Bestimmen Sie die Feldstärke gleichmäßig verteilt. Bestimmen Sie die Feldstärke 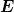 im Abstand im Abstand  vom Draht für vom Draht für  . .
(Anleitung: Betrachten Sie die Ladungsdichte auf der Oberfläche eines Zylinders mit dem Radius  ) ) |
Da  sind die Feldlinien am "Ende" des Drahtes zu vernachlässigen bzw. obsolet. sind die Feldlinien am "Ende" des Drahtes zu vernachlässigen bzw. obsolet.


Nun stellen sich mehrere Probleme:
1. Durch die Anleitung. Soll die Fläche in der Ladungsdichte von eigentlich  vom Coulomb-Gesetz auf vom Coulomb-Gesetz auf  reduziert werden? Ich hätte dabei ein mulmiges Gefühl im Magen. reduziert werden? Ich hätte dabei ein mulmiges Gefühl im Magen.
2. Ferner ist ja die Ladung Q gleichmäßig auf der Länge l und dem Radius r des Drahtes verteilt - im Unterricht haben wir letztens einen symmetrischen "Ladungsblock" zu einer Punktladung zusammengefasst, darf man das bei diesem "langen" Leiter auch machen?
Denken wir uns den Leiter als x-Achse eines Koordinatensystems, ist die Feldstärke in gleicher Höhe (gleicher y-Wert) an egal welcher Stelle (beliebiger x-Wert) konstant?
Wenn ja, dürfte ich doch die Ladungen zusammenfassen. Also die jetzt auf der Länge l verteilte Ladung zu einer Gesamt-Punktladung.
Ein kleiner Denkanstoß eurerseits?  |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 15. Okt 2008 16:12 Titel: Re: E-Feld eines zylindrischen Drahtes schnudl Verfasst am: 15. Okt 2008 16:12 Titel: Re: E-Feld eines zylindrischen Drahtes |
 |
|
Ist dir der Satz von Gauss ein Begriff?
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
Herbststurm

Anmeldungsdatum: 05.09.2008
Beiträge: 412
Wohnort: Freiburg i. Brsg.
|
 Herbststurm Verfasst am: 15. Okt 2008 16:12 Titel: Herbststurm Verfasst am: 15. Okt 2008 16:12 Titel: |
 |
|
Hi,
Das Feld ist einfach der negative Gradient des Potentials. Hier interessiert sogar nur eine Komponente, also das Potential nach dem axialen Einheitsvektor ableiten. Das ganze machst du am besten in Zylinderkoordinaten. Dann musst du das Feld ja nur entlang eines Basisvektors bestimmen, da dir der Rest hier egal sein kann.
Dein Potential ist ja:
 = \int \frac{\varrho(r')}{|r-r'|} ~ \mathrm{d}^{3}r' )
Da die Ladungsdichte einsetzen. Diese ist bei einem dünnen Draht der länge l: (Wegen der Symetrie)
 = \frac{Q}{l}\delta(x)\delta(y)\Theta(\frac{l}{2}-|z|) )
Das Integral lässt sich gut berechnen. Die Delta Funktion kannst direkt ausführen. Dann musst nur noch die Komponente des Gradienten bilden für dien axialen Einheitsvektor.
Gruß |
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2903
Wohnort: München
|
 isi1 Verfasst am: 15. Okt 2008 16:43 Titel: Re: E-Feld eines zylindrischen Drahtes isi1 Verfasst am: 15. Okt 2008 16:43 Titel: Re: E-Feld eines zylindrischen Drahtes |
 |
|
| wishmoep hat Folgendes geschrieben: | 1. Durch die Anleitung. Soll die Fläche in der Ladungsdichte von eigentlich  vom Coulomb-Gesetz auf vom Coulomb-Gesetz auf  reduziert werden? Ich hätte dabei ein mulmiges Gefühl im Magen. reduziert werden? Ich hätte dabei ein mulmiges Gefühl im Magen. |
Das mulmige Gefühl ist ganz unnötig:
Im Kugelfall ist die Oberfläche 4pi r² und beim Zylinder eben 2pi r l ... unter Vernachlässigung der Enden.
Und durch diese Oberfläche A muss die Verschiebung: A * D = Q
Ist das verständlich?
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
Herbststurm

Anmeldungsdatum: 05.09.2008
Beiträge: 412
Wohnort: Freiburg i. Brsg.
|
 Herbststurm Verfasst am: 15. Okt 2008 16:55 Titel: Re: E-Feld eines zylindrischen Drahtes Herbststurm Verfasst am: 15. Okt 2008 16:55 Titel: Re: E-Feld eines zylindrischen Drahtes |
 |
|
| schnudl hat Folgendes geschrieben: | | Ist dir der Satz von Gauss ein Begriff? |
Du meinst schon Gesetz und nicht Satz oder?
Gauß'scher Satz heisst doch einfach nur, dass man aus einem Volumenintegral über die Divergenz ein Oberflächenintegral bekommt, während das Gauß'sche Gesetz die integrale Form der ersten Maxwell Gleichung ist.
Oder habe ich da was verwechslt? 
Zuletzt bearbeitet von Herbststurm am 15. Okt 2008 16:56, insgesamt 2-mal bearbeitet |
|
 |
wishmoep
Anmeldungsdatum: 07.09.2008
Beiträge: 1342
Wohnort: Düren, NRW
|
 wishmoep Verfasst am: 15. Okt 2008 16:55 Titel: wishmoep Verfasst am: 15. Okt 2008 16:55 Titel: |
 |
|
Hey danke für die Antworten,
nun - da mein Wissen bzgl. Integralrechnung / Vektorrechnung ziemlich rudimentär ist - was wohl auch daran liegt, dass ich grade "erst" in der 12 Klasse bin mit Ph/M-LK - kann ich den Satz von Gauß nicht auswendig, habe aber schon von ihm gehört.
Zum Thema Divergenzen / Gradienten kann ich ja beruhigt den mathematischen Teil vom Nolting nutzen, obwohl das schon schwer zu verdauen ist. Nichts desto trotz, zu dir Herbststurm.
Was ist dein 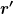 im Integral? Das ungestrichene r ist ja wohl der Radius vom Draht. im Integral? Das ungestrichene r ist ja wohl der Radius vom Draht.
Warum wir die 3 ) dort stehen haben ist mir - so denke ich - klar. dort stehen haben ist mir - so denke ich - klar.
Denn:

Und somit
\,\mathrm{d}^3\vec{r}=\iiint\,\vec{F}(x,y,z)\,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z)
Des Weiteren vermisse ich bei deinem Potential 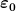 . Ist das iwo verloren gegangen? . Ist das iwo verloren gegangen?
Wir haben das el. Potential für ein Coulomb-Feld so hergeleitet:
\,\mathrm{d}s)
Für p_0 im Unendlichen dann:

Zu isi's Vorschlag.
Das D bezieht sich bei dir auf die erste Maxwell'sche Gleichung?
Bzw. auf die elektrische Flussdichte? |
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2903
Wohnort: München
|
 isi1 Verfasst am: 15. Okt 2008 19:04 Titel: Re: E-Feld eines zylindrischen Drahtes isi1 Verfasst am: 15. Okt 2008 19:04 Titel: Re: E-Feld eines zylindrischen Drahtes |
 |
|
| wishmoep hat Folgendes geschrieben: |
 |
Eigentlich bezog ich mich auf Deine Formel

_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
wishmoep
Anmeldungsdatum: 07.09.2008
Beiträge: 1342
Wohnort: Düren, NRW
|
 wishmoep Verfasst am: 15. Okt 2008 19:05 Titel: wishmoep Verfasst am: 15. Okt 2008 19:05 Titel: |
 |
|
Ja gut - fürs Vakuum gilt auch

Nur würd ich gern die Lösung über den Gradienten und die Poisson-ähnliche-Gleichung verstehen ;-). |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 15. Okt 2008 19:17 Titel: schnudl Verfasst am: 15. Okt 2008 19:17 Titel: |
 |
|
In Worten:
Denk dir einen Zylinder mit Radius r und Länge l, der den Draht koaxial umgibt.
Das gesuchte Feld zeigt aus Symmetriegründen in radialer Richtung und hat überall auf der Zylinderoberfläche den gleichen Betrag und steht normal auf diese.
Das Produkt aus Feld x Fläche muss die gesamte Ladung im Zylinder, geteilt durch die Dielektrizitätskonstante sein.
Allgemein: Das Integral über die Oberfläche eines geschlossenen Volumens über das innere Produkt aus E und die Flächennormale A ergibt die gesamte im Volumen V enthaltene Ladung, geteilt durch die Dielektrizitätskonstante.
Also:

Gauss:

Die beiden Deckel des Zylinders braucht man nicht zu berücksichtigen, da das zur Achse parallele Feld für l >> r verschwindet.
Wie lautet daher E ?
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
wishmoep
Anmeldungsdatum: 07.09.2008
Beiträge: 1342
Wohnort: Düren, NRW
|
 wishmoep Verfasst am: 15. Okt 2008 19:28 Titel: wishmoep Verfasst am: 15. Okt 2008 19:28 Titel: |
 |
|
Wie ich anfangs vermutete:
=\frac{1}{2\,\pi\,l\,\varepsilon_0}\cdot\frac{Q}{r})
Für einen Vektor müsste man noch einen Einheitsvektor definieren. Aber das brauchen wir ja nicht 
Also doch so rum ;-); nur mit einer anderen Vorstellung für den Zylinder.
Danke für die komplizierten und einfachen Hilfen   |
|
 |
|


















