| Autor |
Nachricht |
eifelreh
Anmeldungsdatum: 04.06.2006
Beiträge: 56
|
 eifelreh Verfasst am: 25. Jul 2007 11:40 Titel: E-Feld einer unendlichen Platte |
 |
|
Hallo,
ich sitze da an dieser aufgabe...
Also: es soll das E-feld einer unendlich ausgedehnten platte (in der x-z-ebene) berechnet werden, die die flächenladungsdichte  trägt. Dass da nicht 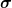 auftaucht, dürfte ein verweis zum Gaußschen gesetz sein...? Na, jedenfalls lautete eine allgemeine empfehlung, bei objekten hoher symmetrie eben dasselbe zu nutzen.
Nun, das ergebnis habe ich ja schon gefunden, für eine klausur muss ich mich aber vermutlich auch auf dem weg auskennen.
Also, allgemein gilt ja erst mal:
= \frac{1}{4 \pi \varepsilon_0} \frac{Q}{r^2} \vec{e}_r.) , sowie
Auch dürfte natürlich das E-Feld allein eines in y-richtung sein, womit sich im Gaußschen gesetz das  doch reduziert auf  ?
Wie aber führe ich eine (über einen geschlossenen kreis gehende) integration  über eine unendliche platte durch...?
Oder ist das wieder so eine 'flache-dose'-chose...die hab ich ja noch nie verstanden... 
Das ergebnis lautet wohl folgendermaßen:
= \frac{\sigma}{2 \varepsilon_0} \frac{y}{|y|} \cdot \vec{e}_y )
Tja, und dann soll im zweiten teil das selbe noch für einen unendlichen, geraden stab in z-richtung mit linienladungsdichte "  " bestimmt werden. Hmm, wahrscheinlich nicht viel anders, nur dass das e-feld wohl in x- und y-richtung radialsysmmetrisch verläuft.
Aber wie lautet der weg...? Könnte da wer helfen...!?
tanx, reh[/latex]
_________________
Wissen ist immer mehr das Wissen von Wissensquellen... |
|
 |
para
Moderator
Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
| para Verfasst am: 25. Jul 2007 12:38 Titel: Re: E-Feld einer unendlichen Platte |
|
|
| eifelreh hat Folgendes geschrieben: | Das ergebnis lautet wohl folgendermaßen:
|
Das stimmt schonmal. ^^
Es gibt mehrere Wege auf die Feldstärke zu kommen, nur manche sind praktikabler als andere. ^^
| eifelreh hat Folgendes geschrieben: | |
Das könnte schwierig werden, da die Fläche ja sicher als unendlich dünn idealisiert wird, damit ist die Raumladungsdichte dort natürlich unendlich groß, was Probleme bei der Rechnung macht. (Wenn man den Ansatz mal an der Lösung ausprobiert, merkt man ja auch dass es dort mit der Stetigkeit der Ableitung schlecht aussieht.)
| eifelreh hat Folgendes geschrieben: | Wie aber führe ich eine (über einen geschlossenen kreis gehende) integration über eine unendliche platte durch...?
Oder ist das wieder so eine 'flache-dose'-chose...die hab ich ja noch nie verstanden... |
Genau, mit Dosen funktioniert das zum Beispiel (Aber auch mit Würfeln, Quadern und sonstigen geraden Prismen ^^). 
Das wichtigste bei solchen Problemen ist eine Vorstellung zu entwickeln, wie das Feld wohl aussehen wird, um die Symmetrie des Problems ausnutzen zu können.– Hier ist es eben entscheidend zu erkennen, dass das Feld aufgrund der homogenen Ladungsverteilung auf der unendlich großen x-z-Ebene an jedem Punkt im Raum wohl nur eine Komponente in y-Richtung haben kann. Alles andere wäre aus Symmetriegründen unlogisch, also wenn auf eine Probeladung irgendwo im Raum auf einmal eine Kraft in x- oder z-Richtung wirken würde. – Des weiteren wird die Feldstärke wohl nur vom Abstand von der Ebene abhängen. Da die Ebene unendlich ausgedehnt ist, bleibt eine Verschiebung in x- oder z-Richtung ja folgenlos. – Die Feldlinien werden logischerweise immer von der Ebene wegzeigen (für positive Flächenladungsdichte) oder immer von ihr wegzeigen.
Schauen wir uns jetzt nochmal den Integralsatz an:Aus den vorherigen Überlegungen wissen wir ja jetzt, dass das E-Feld die folgende Form haben muss:Für Flächen parallel zur x-y- und zur y-z-Ebene ist dieses Integral also offenbar immer Null, da das Feld dort senkrecht zum Flächennormalenvektor steht.
Für Flächen parallel zur x-z-Ebene hingegen vereinfacht sich das Integral deutlich, da dort E-Feld und Normalenvektor parallel sind.
Jetzt sucht man sich eine geeignete geschlossene Oberfläche über die man integriert. Man nehme zum Beispiel einen Würfel mit folgenden Eigenschaften:– Grund- und Deckfläche sind parallel zur x-z-Ebene und haben den jeweils den Abstand y bzw. -y von dieser. – Die Mantelflächen sind jeweils entweder parallel zur x-y- oder zur y-z-Ebene. – Die Flächen haben jeweils den Flächeninhalt A. Jetzt integriert man los. Für die Seitenflächen fallen die Integrale weg. Für Grund- und Deckfläche sehen die Integrale sehr einfach aus, da die Feldstärke entlang dieser Flächen konstant und parallel zum Normalenvektor ist, erhält man einfach jeweils.Als Integral über die gesamt Würfeloberfläche bekommt man also:Die eingeschlossene Ladung in diesem Würfel lässt sich recht problemlos bestimmen:Also wieder Integralsatz im ganzen angeschaut und man erhält:
Das nach dem Betrag der Feldstärke umgestellt führt auf die Lösung. Die Nachfaktoren repräsentieren dann die Überlegungen, dass das Feld immer von der Platte wegzeigt (also die Richtung vom Vorzeichen von y abhängt), und dass das Feld in y-Richtung gerichtet ist.
Jetzt die Dosensache etwas klarer? 
_________________
Formeln mit LaTeX |
|
|
para
Moderator
Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
| para Verfasst am: 25. Jul 2007 12:39 Titel: Re: E-Feld einer unendlichen Platte |
|
|
| eifelreh hat Folgendes geschrieben: | | Tja, und dann soll im zweiten teil das selbe noch für einen unendlichen, geraden stab in z-richtung mit linienladungsdichte " " bestimmt werden. Hmm, wahrscheinlich nicht viel anders, nur dass das e-feld wohl in x- und y-richtung radialsysmmetrisch verläuft. |
Jop, entweder mal selber probieren oder dafür bitte 'nen eigenen Thread eröffnen. ;-)
_________________
Formeln mit LaTeX |
|
|
eifelreh
Anmeldungsdatum: 04.06.2006
Beiträge: 56
|
| eifelreh Verfasst am: 28. Jul 2007 12:55 Titel: |
|
|
Ja,
para, danke für die ausführung, glaube ich hab es jetzt, auch für den zweiten fall. 
reh-tard
_________________
Wissen ist immer mehr das Wissen von Wissensquellen... |
|
|
para
Moderator
Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
| para Verfasst am: 29. Jul 2007 10:52 Titel: |
|
|
Schön, was hast du denn für den zweiten Fall raus? ^^
_________________
Formeln mit LaTeX |
|
|
eifelreh
Anmeldungsdatum: 04.06.2006
Beiträge: 56
|
| eifelreh Verfasst am: 06. Aug 2007 17:21 Titel: |
|
|
der zweite fall... hab es jetzt nicht (mehr...) vorliegen, ging aber ungefähr so:
Integration über den kreisumfang, also 2 Pi mal r um den leiter rum, dieser faktor wird dann in der gleichung rübergebracht, außerdem einfach ein 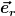 angehängt, das entsprechend die radiale richtung des e-feldes anzeigt.
Also (wenn ich's jetzt noch richtig im kopf habe) einfach:
= \frac{\rho_l}{2 \pi r} \vec{e}_r)
Naja, irgendsowas war es eben
Das eingängige jedenfalls ist, dass das e-feld einer unendlichem platte entfernungsUNabhängig ist (weiter weg sehe/fühle ich als geladenes teilchen kompensierend gleichsam immer mehr von der platte), das des unendlichen geraden drahtes ist 1/r-abhängig, das der homogenen kugel schließlich 1/r^2-abhängig, wie bekannt.
reh-kognite
_________________
Wissen ist immer mehr das Wissen von Wissensquellen... |
|
|
Birsel
Anmeldungsdatum: 07.03.2011
Beiträge: 74
|
| Birsel Verfasst am: 18. Jan 2014 17:47 Titel: |
|
|
Hey, zwar ein altes Thema, aber genau auch mein Problem im Moment.
Ich verstehe den 2. Post von "Para" nicht ganz.
Also wie der Würfel da denn nun im Raum zur Platte liegt. Welche Seite ist denn die Grundseite und der Deckel usw...
Könnte das vielleicht jemand, der das versteht mal kurz skizzieren?
Vielen Dank
Gruß Birsel
|
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
| as_string Verfasst am: 18. Jan 2014 18:32 Titel: |
|
|
Hallo,
Du meinst die unendlich ausgedehnte Flächenladung, richtig?
Das sieht etwa so aus, wie in der Skizze. Dabei liegt die Platte in der x-z-Ebene und die rote Fläche der Box auch, während die Feldlinien in die positive und negative y-Richtung.
Gruß
Marco
| Beschreibung: |
|
Download |
| Dateiname: |
unendl_platte.png |
| Dateigröße: |
40.04 KB |
| Heruntergeladen: |
3806 mal |
|
|
|
Birsel
Anmeldungsdatum: 07.03.2011
Beiträge: 74
|
| Birsel Verfasst am: 18. Jan 2014 21:19 Titel: |
|
|
Hey,
super.
DANKE
Ich hoffe das wir nicht so viel Arbeit.
Eine Frage habe ich jetzt noch. welches sind die 2 Flächen die man zur Berechnung nimmt?
Bei: 2*A*E
Eigentlich die durchfluteten oder? Sprich die bei dir roten?
Gruß Birsel
|
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
| as_string Verfasst am: 18. Jan 2014 22:24 Titel: |
|
|
Ja, genau... Das wollte ich eigentlich noch dazu schreiben, dass es die roten sein soll (die unten kann man aber nicht sehen, die konnte ich dann auch nicht rot machen... )
Und die Flächen sind ja jeweils genau so groß, wie die Fläche der eingeschlossenen Flächenladung. Die kürzt sich also schön raus.
Und weil das Feld homogen sein muss vor so einer unendlichen Platte, ist es sogar egal, wie weit man von der Platte weg ist (in dieser idealisierten Darstellung mit unendlicher Ausdehnung natürlich nur).
Gruß
Marco
|
|
|
Birsel
Anmeldungsdatum: 07.03.2011
Beiträge: 74
|
| Birsel Verfasst am: 19. Jan 2014 08:36 Titel: |
|
|
Hey, super!
DANKE
Wenn man das ganze jetzt mit einem Zylinder macht, dann müssten die Stirnflächen ja auch rot sein und genau gleich orientiert sein?
Denn die Form/größe etc. der Fläche ist ja egal. Wir ja eh gekürzt.
Wichtig aber, es muss ein Geometrie sein, die auf den beiden "durchfluteten" Seiten gerade und gleich groß ist.
Wenn das jetzt richtig ist, habe ich s verstanden
Gruß Birsel
|
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
| as_string Verfasst am: 19. Jan 2014 12:31 Titel: |
|
|
Hallo,
ja, das ist alles richtig. Das ist das, was para so beschrieben hat:
| para hat Folgendes geschrieben: | | Genau, mit Dosen funktioniert das zum Beispiel (Aber auch mit Würfeln, Quadern und sonstigen geraden Prismen ^^). |
Allerdings nur für die Platte. In der Originalfrage war ja noch die Rede von einer unendlichen Ladungsverteilung entlang einer Geraden. Da nimmt man z. B. eine "Dose", bei der jetzt aber die Grund- und Deckfläche nicht durchströmt wird, weil sie senkrecht auf der Ladungsverteilungs-Geraden steht und die Feldlinien dann parallel zu den Grund- und Deckflächen sind, aber der Zylinder-Mantel wird durchströmt. Die Feldlinien stehen auch genau senkrecht auf der Mantelfläche und die Mantelfläche hat überall den selben Abstand zur Ladungsverteilung, so dass es aus Symmetriegründen wieder logisch erscheint, dass dort überall die selbe Feldstärke herrschen muss.
Gruß
Marco
|
|
|
yassin
Anmeldungsdatum: 24.08.2016
Beiträge: 29
|
| yassin Verfasst am: 03. Sep 2016 13:45 Titel: Re: E-Feld einer unendlichen Platte |
|
|
Ich muss auch nochmal diesen alten Thread ausgraben. (Die jenigen die sich darüber Beschweren dass man alte Threads ausgrät sind doch bestimmt die gleichen die immer meckern, dass etwas schon 1000 mal gefragt wurrde  )
Mir ist hier nämlich eine Sache unklar:
Wieso setzt man das E-Feld hier in Betrag?
| para hat Folgendes geschrieben: |  |
Wie ist diese Umformung physikalisch/mathematisch begründet?
Gruß,
Yassin
|
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 03. Sep 2016 14:36 Titel: Re: E-Feld einer unendlichen Platte |
|
|
| para hat Folgendes geschrieben: |
...
Jetzt integriert man los. Für die Seitenflächen fallen die Integrale weg. Für Grund- und Deckfläche sehen die Integrale sehr einfach aus, da die Feldstärke entlang dieser Flächen konstant und parallel zum Normalenvektor ist, erhält man einfach jeweils....
|
|
|
|
yassin
Anmeldungsdatum: 24.08.2016
Beiträge: 29
|
| yassin Verfasst am: 03. Sep 2016 15:57 Titel: |
|
|
|
Sowohl das Vorzeichen des Flächennormalenvektors als auch das Vorzeichen des E-Vektors sind für den Fall negativ und heben sich weg. Deshalb?
|
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 03. Sep 2016 16:06 Titel: |
|
|
| yassin hat Folgendes geschrieben: | | Sowohl das Vorzeichen des Flächennormalenvektors als auch das Vorzeichen des E-Vektors sind für den Fall negativ und heben sich weg. Deshalb? |
Je nachdem auf welcher Seite der Platte Du bist. In jedem Fall zeigen beide immer in dieselbe Richtung.
|
|
|
|
Registrieren
Login
FAQ
Suchen
