Geladener offener Kreis

Gimel · Anmeldungsdatum: 06.11.2007 Beiträge: 96 Wohnort: Wuppertal

Hallo Physiker!
Nehmen wir an, ich hätte einen dünnen nichtleitenden Stab, der zu einem Kreis mit Radius r=50cm gebogen wurde. Allerdings ist er nicht ganz geschlossen, sondern an einer Stelle noch 2cm offen. Die Ladung ( 1 Coulomb ) wäre gleichmäßig über den ganzen Stab verteilt.
Ich will nun die Größe des elektr. Feldes am Kreismittelpunkt bestimmen.
Die Feldlinien gehen ja alle orthogonal vom Ring weg. Würden sich dann die in der Mitte so aufheben, dass nur das der Lücke gegenüberliegende Stück Stab ein elektr. Feld am Kreismittelpunkt erzeugen würde?
Ist das der richtige Ansatz?

schnudl · Moderator Anmeldungsdatum: 15.11.2005 Beiträge: 6979 Wohnort: Wien

ja, es gilt ja das Überlagerungsprinzip für Felder.

Gimel · Anmeldungsdatum: 06.11.2007 Beiträge: 96 Wohnort: Wuppertal

Wäre dann folgendes richtig:

Radius: r=0,5m
Lücke: d=0,2m

Umfang:

Ladung pro Längeneinheit:

Hier ist mir klar, dass d nicht ganz korrekt ist, da der Kreis ansich eine Krümmung hätte. Aber imo ist die so minimal hier, dass man das Stückchen ruhig als grade ansehen könnte.
Nun neutralisieren sich die Feldlinien bis auf die vom Stückchen s: s=d
Davon erzeugt jedes ds ein kleines Elektrisches Feld:

Durch Integrieren kommen wir auf:

So dass wir am Ende erhalten: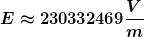

Ist dies richtig? Kommt mir irgendwie seltsam vor. Ich bin bei der Sache mit der Krümmung nicht ganz zufrieden.
Könnte mir vllt einer sagen, wie ich die miteinbinden könnte?

schnudl · Moderator Anmeldungsdatum: 15.11.2005 Beiträge: 6979 Wohnort: Wien

Ich denke deine Überlegung ist richtig.
Ich denke auch, dass man keinen grossen Fehler macht, wenn die Krümmung nicht berücksichtigt wird.

Gimel · Anmeldungsdatum: 06.11.2007 Beiträge: 96 Wohnort: Wuppertal

Gäbe es denn eine Möglichkeit mit den gegebenen Werten auf den Winkel

zu schließen über den ich dann integrieren könnte, um ein genaueres Ergebnis zu erzielen?
Denn so wie ich das hier gerechnet habe, verhält es sich genauso wie bei einer Punktladung im Abstand r

Also

soll der Winkel des Ausschnitts sein. Dann könnte ich

mit ds in Verbindung setzen und hätte somit beim Integrieren wohl was trigonometrisches, so dass das Verhalten nicht mehr gleich dem einer Punktladung wäre.

schnudl · Moderator Anmeldungsdatum: 15.11.2005 Beiträge: 6979 Wohnort: Wien

Das ist ganz und gar nicht schwierig: zeichne dir mal in einer Skizze auf, welche Anteile im Summationspunkt überlagert werden. Du solltest sehen, dass nur jene Anteile einen Beitrag in Radialkomponente liefern, welche parallel zur Spiegel-Symmetrielinie des Kreissegments liegen. Wie bekommt man diese Komponente?

Gimel · Anmeldungsdatum: 06.11.2007 Beiträge: 96 Wohnort: Wuppertal

schnudl · Moderator Anmeldungsdatum: 15.11.2005 Beiträge: 6979 Wohnort: Wien

Hast du die Symmetrie schon erkannt. Die Feldbeiträge senkrecht zur Symmetrieachse heben sich gegenseitig auf, es bleibt nur die parallele Komponente. Hier geht der cos eines Winkels ein.

AUFZEICHNEN !

Gimel · Anmeldungsdatum: 06.11.2007 Beiträge: 96 Wohnort: Wuppertal

Hmmm, - hab grade gesehen, das es ja eine ganz simple Formel für den Kreisbogen gibt, die den Winkel beinhaltet.

http://upload.wikimedia.org/math/2/1/e/21e2befa9b0fab170ed3cfb2c6a11907.png

Aber hab das Bild jetzt nochmal in paint gezeichnet:

http://img132.imageshack.us/img132/9886/kreisak3.th.png

Rot ist der Teil, der das Elektr. Feld erzeugt.
Grün ist der Winkel phi.
Blau ist die Symmetrieachse des Ausschnitts.

Verstehe auch, dass von den Feldlinien nur die zur Symmetrieachse parallelen Komponenten die Feldstärke bestimmen. Aber ich finde da einfach nicht den Zusammenhang mit dem Winkel bzw. den Cosinus.

schnudl · Moderator Anmeldungsdatum: 15.11.2005 Beiträge: 6979 Wohnort: Wien

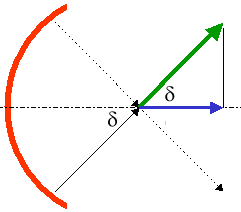
hilft das?

Von allen (grünen) Beiträgen addiert sich nur die blaue Komponente zu einem resultierenden Feld. Wie bestimmst du die Längde des blauen Pfeils, wenn der Winkel und die Länge des grünen Pfeils gegeben ist?

Gimel · Anmeldungsdatum: 06.11.2007 Beiträge: 96 Wohnort: Wuppertal

Ja der Cosinus des Winkels ist die Ankathete durch die Hypotenuse.
Somit könnte ich den blauen Pfeil berechnen.
Allerdings habe ich ja den Winkel und überlege die ganze Zeit wie ich an den rankommen kann.

Versuch das jetzt noch mit der Formel für den Kreisbogen und die Kreissehne.

EDIT
Hab jetzt die Formeln für den Kreisbogen und die Kreissehne und muss sagen, dass da doch ein recht großer unterschied ist. Und zwar beträgt die feldstärke nun 229597737.1 V/m statt 230332469 V/m .
Kann natürlich sein, dass das kein so großer Unterschied ist.... kenn mich da nicht so aus Schläfer

schnudl · Moderator Anmeldungsdatum: 15.11.2005 Beiträge: 6979 Wohnort: Wien

Wie sieht denn der exakte Audruck für das E im Mittelpunkt aus?
Es geht hier nicht um Erraten sonder um das systematische Aufstellen eines (elementaren) Integrals. Big Laugh

Du hast ja oben schon so schön begonnen - mach in diesem Sinne weiter!

Gimel · Anmeldungsdatum: 06.11.2007 Beiträge: 96 Wohnort: Wuppertal

Oh da war nichts geraten. Habe nur einfach keine Ahnung von trigonometrie und dergleichen.
Aber nachdem ich mir die Formeln für den Kreisbogen angeguckt habe, hab ich einen Ansatz gefunden. Mit diesem hab ich auch ein schönes Integral gebildet und kam so auf mein Ergebnis Augenzwinkern

Deinen Ansatz kann ich ( Mittlerweile Big Laugh

) nachvollziehen. Allerdings kommt es mir so vor als wären damit noch nicht alle unbekannten geklärt, so dass man die Formeln des Kreisbogens noch benutzen muss.