| Autor |
Nachricht |
ErebosChaos
Anmeldungsdatum: 19.12.2007
Beiträge: 4
|
 ErebosChaos Verfasst am: 19. Dez 2007 11:52 Titel: Wasserstoff, Eigenfunktion |
 |
|
Hallo liebes Forum,
ich habe mich gerade bei euch angemeldet, da ich beim folgenden Problem überhaupt nicht mehr weiterkomme und unglaublich verzweifelt bin!!
im Buch Quantenmechanik von Gerald Grawert
findet sich für die Eigenfunktion von Wasserstoff
Psi_{1,0,0}(Vektor x) = Wurzel(1/(Pi*r0^3)*exp(-r/r0)
Die Wahrscheinlichkeitsdichte des Impulses wird mit
PsiSchlange_{1,0,0}(Vektor p) = 2^(3/2)/Pi * (hquer/r0)^(5/2) * (p^2+(hquer^2/r0^2))^-2
angegeben. Um von Gleichung 1 auf Gl 2 zu kommen wurde die Fourier-Transformatiom genutzt.
Ich komme aber nicht auf das Ergebnis. Vielleicht kann mir jemand helfen?!
Vielen lieben Dank für eure Antworten!
ErebosChaos
|
|
 |
mitschelll
Anmeldungsdatum: 06.12.2007
Beiträge: 362
|
| mitschelll Verfasst am: 19. Dez 2007 12:15 Titel: |
|
|
Wo hast Du denn Probleme? Ist unklar, was mit Fourier-Transformation gemeint ist oder sind die Rechnungen nicht nachvollziehbar?
Prinzipiell muss die Wellenfunktion in Ortsdarstellung mittels der Fourier-Transformation in die Impulsdarstellung transformiert werden. Hier wurde speziell die Wellenfunktion mit den Quantenzahlen n=1, l=0 und m=0 betrachtet.
|
|
|
ErebosChaos
Anmeldungsdatum: 19.12.2007
Beiträge: 4
|
| ErebosChaos Verfasst am: 19. Dez 2007 12:21 Titel: |
|
|
|
Das Problem ist das ich nicht weiss, wie man von Gleichung 1. zur Gleichung 2. die Fourier-Transformation durchführt. Man hat ja das Problem der karthesischen und radialen Koordinaten das man berücksichtigen muss.
|
|
|
schnudl
Moderator
Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
| schnudl Verfasst am: 19. Dez 2007 13:29 Titel: Re: Wasserstoff, Eigenfunktion |
|
|
Ich habe mir mal erlaubt die Gleichungen in LaTex umzuschreiben, damit man nicht schon beim ersten Betrachten die Freude an der interessanten Rechnung verliert:
| ErebosChaos hat Folgendes geschrieben: | Hallo liebes Forum,
ich habe mich gerade bei euch angemeldet, da ich beim folgenden Problem überhaupt nicht mehr weiterkomme und unglaublich verzweifelt bin!!
im Buch Quantenmechanik von Gerald Grawert
findet sich für die Eigenfunktion von Wasserstoff
 = \sqrt{\frac{1}{\pi r_0^3}} \, \exp(-r/r_0))
Die Wahrscheinlichkeitsdichte des Impulses wird mit
 = 2^{3/2}/\pi \cdot \left(\hbar/r_0\right)^{5/2} \cdot \left(p^2+\left( \hbar^2/r_0^2\right) \right)^{-2})
angegeben. Um von Gleichung 1 auf Gl 2 zu kommen wurde die Fourier-Transformatiom genutzt.
Ich komme aber nicht auf das Ergebnis. Vielleicht kann mir jemand helfen?!
Vielen lieben Dank für eure Antworten!
ErebosChaos |
Wie hast du denn den Ansatz gemacht ?
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
|
ErebosChaos
Anmeldungsdatum: 19.12.2007
Beiträge: 4
|
| ErebosChaos Verfasst am: 19. Dez 2007 14:21 Titel: |
|
|
Vielen Dank für das Umschreiben!
Also die Aufgabe ist folgende:
Betrachten Sie ein Wasserstoffatom im Zustand |n,l,m>=|1,0,0>.
1. Berechne den mittleren abstand (Erwartungswert) des Elektrons vom Atomkern.
2. Berechne die Wahrscheinlichkeitsverteilung des (radialen!!!) Impulses.
3. Finde den Erwartungswert des (radialen) Impulses.
4.Zeige: <r><p>=4hquer
Meine Lösung für Nr.1 ist folgende(siehe anhang).
Bei der Nr.2 kenn ich sozusagen das Ergebnis jedoch nicht die Herleitung(siehe bereits beschriebenes Problem oben).
Wie immer VIELEN DANK im VORAUS für jegliche Hilfe!
| Beschreibung: |
|
Download |
| Dateiname: |
mittlererAbstand.doc |
| Dateigröße: |
19 KB |
| Heruntergeladen: |
422 mal |
|
|
|
schnudl
Moderator
Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
| schnudl Verfasst am: 19. Dez 2007 16:12 Titel: |
|
|
für die Wahrscheinlichkeitsverteilung des Impulses brauchst du nicht in den Impulsraum wechseln! Es gibt ja den Impulsoperator auch im Ortsraum !
Weisst du wie der aussieht ?
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
|
schnudl
Moderator
Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
| schnudl Verfasst am: 19. Dez 2007 18:31 Titel: |
|
|
Das hatten wir hier schon mal...zumindest Aufgabe 1)
Aufgabe 2) ist analog. 
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
|
ErebosChaos
Anmeldungsdatum: 19.12.2007
Beiträge: 4
|
| ErebosChaos Verfasst am: 20. Dez 2007 16:22 Titel: |
|
|
Vielen Dank für jegliche Hilfe. Das Problem ist gelöst und die Aufgabe zu Ende gerechnet. Falls Interesse besteht kann ich die Ergenisse denächst einscannen.
Vielen Dank nochmal!
|
|
|
Saga
Gast
|
| Saga Verfasst am: 24. Nov 2010 20:37 Titel: |
|
|
Hi
Sorry für den alten Thread, ich wollte keinen neuen aufmachen.
Ich habe ein Problem mit dem oben genannten Beispiel 2:
"Berechne die Wahrscheinlichkeitsverteilung des Impulses eines Elektrons im Grundzustand des Wasserstoffatoms."
Diese Frage ist ja hier im Thread nicht gelöst worden.
Ich kenne die Wellenfunktion und kann den Wahrscheinlichkeitswert für den Impuls mit
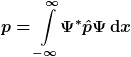
berechnen. Aber wie komme ich dann auf die Wahrscheinlichkeitsverteilung?
Ich komm bei dem Problem einfach nicht weiter obwohls wahrscheinlich eh so einfach sein wird.
Bitte um Hilfe.
|
|
|
|
Registrieren
Login
FAQ
Suchen
