| Autor |
Nachricht |
Gargy
Anmeldungsdatum: 24.11.2006
Beiträge: 1046
|
 Gargy Verfasst am: 29. Mai 2007 17:53 Titel: Kreisring und sein Feld |
 |
|
Hallo, ich bräuchte mal einen Gedankenschubser für folgende Aufgabe:
Ein dünner Kreisring mit dem Radius a trägt die Ladung Q (gleichförmig verteilt). Zu bestimmen ist das elektrische Feld im Punkt P auf der Symmetrieachse im Abstand x vom Mittelpunkt des Rings. Ladung pro Längeneinheit sei  .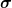
Kann mir jemand einen Tipp geben, wie ich da anfange? Ich habe schon soviel rumprobiert, dass mittlerweile alles falsch zu sein scheint. Vielleicht hilft mal ein anderer Gedankengang...
Hilfe wäre also super! 
|
|
 |
para
Moderator
Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
| para Verfasst am: 29. Mai 2007 18:56 Titel: Re: Kreisring und sein Feld |
|
|
Welche Symmetrieachse ist denn gemeint? Eine in der Ringebene oder die senkrecht zur Ringebene?
_________________
Formeln mit LaTeX |
|
|
Gargy
Anmeldungsdatum: 24.11.2006
Beiträge: 1046
|
| Gargy Verfasst am: 29. Mai 2007 19:09 Titel: |
|
|
so in etwa...
| Beschreibung: |
|
Download |
| Dateiname: |
E-Feld.GIF |
| Dateigröße: |
3.73 KB |
| Heruntergeladen: |
4569 mal |
|
|
|
para
Moderator
Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
| para Verfasst am: 29. Mai 2007 19:21 Titel: |
|
|
Naja, das sieht doch in der Skizze schonmal sehr gut aus - viel gibt's dazu jedenfalls nicht mehr zu sagen. ^^
Ich denke du hast schon gesehen dass sich die Feldanteile senkrecht zur Achse jeweils kompensieren, also genügt es die Feldanteile entlang der Achse zu betrachten. Für eine kleine Ladung dQ auf dem Kreisring gilt dann gemäß deiner Skizze:Mit k als Coulombkonstante.
Da sich ja die Felder aller Teilladungen superponieren, musst du jetzt irgendwie über alle Teilladungen summieren, bzw. bei kontinuierlicher Verteilung eben integrieren. Ob du dazu jetzt vorher noch dQ über ein dl ausdrückst und über den Vollkreis integrierst, oder ob du das Ergebnis aus Symmetriegründen gleich siehst, ist dabei dir überlassen. Die Hauptüberlegung steckt ja darin, welche Feldanteile man betrachten muss, und welche man weglassen kann.
_________________
Formeln mit LaTeX |
|
|
Gargy
Anmeldungsdatum: 24.11.2006
Beiträge: 1046
|
| Gargy Verfasst am: 29. Mai 2007 21:13 Titel: |
|
|
Hm, ja, ok, diese Formel hatte ich auch, aber wie weiter?
Da ich ja die Ladung pro Längeneinheit als 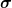angeben soll, muss ich dQ wohl ersetzen, aber irgendwie bin ich da wohl nicht zu in der Lage.
Ich habe einfach so weitergemacht:
Aber irgendwie erscheint mir das falsch. Das sieht aus, als müsste ich über den Kreisradius integrieren... aber der ist doch konstant.
Dann habe ich noch versucht das  anders auszudrücken:
 \cdot x)
} ~ d \phi)
Das ergibt dann aber leider irgendwas kompliziertes und irgendwie habe ich das Gefühl, dass es falsch ist:
} ~ d \phi \cdot \frac{x}{r})
Wenn man's noch etwas schöner schreibt, dann sieht das so aus:
} ~ d \phi )
Kann das richtig sein? Irgendwie... 
|
|
|
para
Moderator
Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
| para Verfasst am: 29. Mai 2007 21:33 Titel: |
|
|
| Gargy hat Folgendes geschrieben: | Ich habe einfach so weitergemacht:
|
Bei der ersten Ersetzung gehe ich noch mit, aber die Ersetzung von dl würde ich mir nochmal ansehen.
Wie bist du auf diesen Ansatz gekommen? Man sollte immer im Hinterkopf behalten worüber man eigentlich integrieren muss, um alle Ladungen zu erfassen, das muss sich auch in der Ersetzung irgendwo wiederfinden.
Ich würde eher folgende Ersetzung vornehmen:Dabei ist Alpha der Winkel zwischen einer vertikalen Achse und dem Ortsvektor zu einer Ladung dQ auf dem Kreisring. (Damit würde man dann anstatt von 0 bis 2*Pi*r von 0 bis 2*Pi integrieren.)
Es lässt sich jetzt vielleicht schwierig erklären, von der Anschaulichkeit her. Eventuell sollte man doch noch einmal einen Schritt zurückzugehen, und ohne die Vereinfachungen versuchen das Ganze allgemeiner zu rechnen. Je nachdem was dir einleuchtender erscheint.
_________________
Formeln mit LaTeX |
|
|
Gargy
Anmeldungsdatum: 24.11.2006
Beiträge: 1046
|
| Gargy Verfasst am: 30. Mai 2007 12:57 Titel: |
|
|
Hm, also ehrlich gesagt, klingt das schon sehr einleuchtend. Ungefähr so hatte ich versucht einen Ansatz zu finden, aber ich wußte nicht wie. Gefällt mir besser als meine Ersetzung.
auf die kam ich übrigens (das sie falsch sein muss war mir irgendwie klar), weil ich mir dachte der Umfang berechnet sich doch folgendermaßen:
einmal abgeleitet...
Das sieht schon so blöde aus, ist bestimmt auch mehr als peinlich, dass hier überhaupt reinzustellen, aber mir fehlt da das Lichtchen, warum das so falsch ist.
edit// ja, alles klar, is ja logisch  ich will ja um den kreis und nicht über den radius 
Zuletzt bearbeitet von Gargy am 30. Mai 2007 20:56, insgesamt einmal bearbeitet |
|
|
Gargy
Anmeldungsdatum: 24.11.2006
Beiträge: 1046
|
| Gargy Verfasst am: 30. Mai 2007 20:54 Titel: |
|
|
So,
 \cdot \sqrt{x²+a²}} ~ \int_{0}^{2 \pi} ~ d \alpha)
 \cdot \sqrt{x²+a²}} \cdot 2 \pi)
k hat ja auch noch einen Wert...
 \cdot \sqrt{x²+a²}} \cdot 2 \pi)
 \cdot \sqrt{x²+a²}})
Kann mir jemand sagen, ob das hinkommt. Irgendwie ist mir das zu lang für eine Lösung 
Kann man das noch vereinfachen?
|
|
|
Gargy
Anmeldungsdatum: 24.11.2006
Beiträge: 1046
|
| Gargy Verfasst am: 30. Mai 2007 22:21 Titel: |
|
|
|
|
|
para
Moderator
Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
| para Verfasst am: 30. Mai 2007 22:56 Titel: |
|
|
Es stimmt, das schwierige bei solchen Aufgaben ist es im Auge zu behalten, worüber man integriert und entlang welchen Weges / in welchen Grenzen man das tun muss, um den Sachverhalt entsprechend auszudrücken. Die Sache ist, dass man diese Ersetzungen eben oft "nach Gefühl" macht, aber dabei stets im Hinterkopf haben muss, was in Form eines Integrals eigentlich dahintersteht - sonst kann es eben passieren dass man zwar vielleicht ein Ergebnis bekommt, das aber mit der Aufgabe nicht mehr viel zu tun hat.
Aber es ist richtig was du gesehen hast. In diesem Fall wäre es nicht sehr sinnvoll über den Radius, also von innen nach außen, zu integrieren (bei anderen Aufgaben sähe das schon anders aus). Hier wäre eben die Integration über den Kreisring, quasi rundherum, sinnvoll und zielführend.
Dein Ergebnis sieht doch schon sehr gut aus. Wenn dir die Form noch nicht gefällt kannst du ja noch ein bisschen drin rumschreiben. ^^Gegebenenfalls noch Zurückersetzen mit k würde eine noch kompaktere Form liefern.
Dass das Ergebnis stimmt kann man an verschiedenen Stellen nachlesen (z.B. hier, Aufgabe 4), das ist wohl eine äußerst beliebte Aufgabe. 
_________________
Formeln mit LaTeX |
|
|
Gargy
Anmeldungsdatum: 24.11.2006
Beiträge: 1046
|
| Gargy Verfasst am: 31. Mai 2007 07:57 Titel: |
|
|
Super, vielen Dank für die Hilfe!
|
|
|
|
Registrieren
Login
FAQ
Suchen
