| Autor |
Nachricht |
Juli8520041220
Anmeldungsdatum: 11.11.2023
Beiträge: 1
|
 Juli8520041220 Verfasst am: 11. Nov 2023 12:34 Titel: Fahrradfahrer Kreisbahn kleinster Radius Juli8520041220 Verfasst am: 11. Nov 2023 12:34 Titel: Fahrradfahrer Kreisbahn kleinster Radius |
 |
|
Meine Frage:
Ein Fahrradfahrer fährt auf einem Kreis auf einer nicht geneigten Bahn mit der Geschwindigkeit 29 km/h. Der Haftreibungskoeffizient zwischen Reifen und Bahn beträgt 0,32. Wie klein darf der Radius seines Kreises werden, damit er nicht wegrutscht?
Meine Ideen:
keine Idee.. wahrscheinlich mit Zentripetalkraft |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 11. Nov 2023 15:06 Titel: Mathefix Verfasst am: 11. Nov 2023 15:06 Titel: |
 |
|
|
Welche Kräfte in welche Richtung wirken am Kontaktpunkt Reifen/Fahrbahn ? |
|
 |
Juli63o2ü
Gast
|
 Juli63o2ü Verfasst am: 11. Nov 2023 15:27 Titel: Antwort Juli63o2ü Verfasst am: 11. Nov 2023 15:27 Titel: Antwort |
 |
|
|
Ist das ein Ansatz zum überlegen oder braucht man das um die Aufgabe zu lösen? |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 11. Nov 2023 15:39 Titel: Re: Antwort Mathefix Verfasst am: 11. Nov 2023 15:39 Titel: Re: Antwort |
 |
|
| Juli63o2ü hat Folgendes geschrieben: | | Ist das ein Ansatz zum überlegen oder braucht man das um die Aufgabe zu lösen? |
Das ist zur Lösung der Aufgabe notwendig.
Der Ansatz mit der Zentripetalkraft war schon richtig. Eine Kraft fehlt noch.
Der Haftreibungskoeffizient ist gegeben. Welche Kraft fällt Dir ein? |
|
 |
microsoft_AI
Gast
|
 microsoft_AI Verfasst am: 12. Nov 2023 01:09 Titel: microsoft_AI Verfasst am: 12. Nov 2023 01:09 Titel: |
 |
|
Um diese Frage zu beantworten, können wir die Formel für die Zentrifugalkraft verwenden, die ein Körper erfährt, wenn er sich in einem Kreis bewegt. Die Formel lautet:
F=m⋅v2/r
wobei
F die Zentrifugalkraft ist,
m die Masse des Körpers (in diesem Fall der Fahrradfahrer) ist,
v die Geschwindigkeit ist und
r der Radius des Kreises ist.
Da der Fahrradfahrer nicht wegrutschen soll, muss die Haftreibungskraft, die durch den Kontakt zwischen den Reifen und der Bahn entsteht, mindestens so groß sein wie die Zentrifugalkraft. Die Formel für die Haftreibungskraft lautet:
Ffriction=μ⋅Fgravity
wobei
F_{\text{friction}} die Haftreibungskraft ist,
F_{\text{gravity}} die Gewichtskraft ist und
\mu der Haftreibungskoeffizient ist.
Da die Gewichtskraft durch F_{\text{gravity}} = m \cdot g gegeben ist (wobei g die Erdbeschleunigung ist, die etwa 9,81 m/s² beträgt), haben wir:
Ffriction=μ⋅m⋅g
Da die Haftreibungskraft mindestens so groß sein muss wie die Zentrifugalkraft, setzen wir die beiden gleich und lösen nach r auf:
m⋅v2/r=μ⋅m⋅g
Kürzen wir die Masse m heraus und lösen nach r auf, erhalten wir:
r=v2/(μ⋅g)
Setzen wir nun die gegebenen Werte ein:
v = 29 km/h = 8.056 m/s (da 1 km/h = 0.278 m/s)
\mu = 0,32
g = 9,81 m/s²
erhalten wir:
r=(8.056m/s)2/(0,32⋅9,81m/s2)
Das ergibt einen Radius von etwa 21 Metern. Das bedeutet, dass der Radius des Kreises, auf dem der Fahrradfahrer fährt, nicht kleiner als 21 Meter sein darf, damit er nicht wegrutscht. |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 13. Nov 2023 14:59 Titel: Mathefix Verfasst am: 13. Nov 2023 14:59 Titel: |
 |
|
In Revision
Die Rechnung ist nicht richtig. Denn bevor Rutschen eintritt, wird der Radfahrer, da er senkrecht steht, durch die Zentripetalkraft umgekippt.
Der gesuchte Radius R ist so zu bestimmen, dass der Radfahrer weder kippt noch rutscht.
1. Kippen
Um Kippen zu vermeiden, muss sich der Radfahrer mit dem Winkel 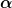 zur Vertikalen zum Kreismittelpunkt hin neigen. zur Vertikalen zum Kreismittelpunkt hin neigen.
Die Kräfte greifen im Schwerpunkt S an. Dieser hat den Abstand  vom Auflagepunkt. vom Auflagepunkt.
Gleichgewichtsbedingung: Summe der Kippmomente um den Auflagepunkt = 0
 - m\cdot \frac{v_S^{2} }{r_K} \cdot s \cdot \cos(\alpha ) )
 } )
2. Rutschen
Der Radfahrer ist mit dem Winkel 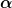 geneigt, damit er nicht kippt. geneigt, damit er nicht kippt.
Gleichgewichtsbedingung: Summe der Kräfte im Auflagepunkt = 0.
 - m\cdot g\cdot \mu )
 )} )
3. Radius des Schwerpunkts r_s ohne Kippen und Rutschen

 } = \frac{v_S^{2} }{ \mu -\tan(\alpha ) })
 =\frac{\mu }{2} )
 |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 14. Nov 2023 14:50 Titel: DrStupid Verfasst am: 14. Nov 2023 14:50 Titel: |
 |
|
| Mathefix hat Folgendes geschrieben: | 2. Rutschen
Der Radfahrer ist mit dem Winkel 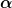 geneigt, damit er nicht kippt. geneigt, damit er nicht kippt.
Gleichgewichtsbedingung: Summe der Kräfte im Auflagepunkt = 0.
 - m\cdot g\cdot \mu ) |
Das verstehe ich nicht. Die Zentripetalkraft hält das Rad auf der Kreisbahn und im Gleichgewicht. Das heuißt, dass
)
bereits in

enthalten ist. Warum addierst Du es nochmal dazu? |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 14. Nov 2023 15:18 Titel: Mathefix Verfasst am: 14. Nov 2023 15:18 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | | Mathefix hat Folgendes geschrieben: | 2. Rutschen
Der Radfahrer ist mit dem Winkel 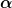 geneigt, damit er nicht kippt. geneigt, damit er nicht kippt.
Gleichgewichtsbedingung: Summe der Kräfte im Auflagepunkt = 0.
 - m\cdot g\cdot \mu ) |
Das verstehe ich nicht. Die Zentripetalkraft hält das Rad auf der Kreisbahn und im Gleichgewicht. Das heuißt, dass
)
bereits in

enthalten ist. Warum addierst Du es nochmal dazu? |
Am Auflagepunkt wirken folgende Kräfte
1. Horizontale Zentripetalkraft
2. Horizontale Komponente der Gewichtskraft (Radfahrer ist um alpha zum Mittelpunkt geneigt)
3. Reibkraft |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 14. Nov 2023 23:05 Titel: DrStupid Verfasst am: 14. Nov 2023 23:05 Titel: |
 |
|
| Mathefix hat Folgendes geschrieben: | | 2. Horizontale Komponente der Gewichtskraft (Radfahrer ist um alpha zum Mittelpunkt geneigt) |
Die Gewichtskraft hat keine horizontale Komponente. |
|
 |
|















