| Autor |
Nachricht |
Nikolas
Ehrenmitglied
Anmeldungsdatum: 14.03.2004
Beiträge: 1873
Wohnort: Freiburg im Brsg.
|
 Nikolas Verfasst am: 13. Nov 2006 15:17 Titel: E-Feld und Ladungsdichte des H-Atoms |
 |
|
Hallo. Zurzeit scheiter ich an folgender Aufgabe:
Gegeben ein elektrisches Feld =q\exp(-\alpha r)\vec{r}/r^2)
1) Berechnen Sie die entsprechende Ladungsdichte.
2) Zeigen Sie, dass die Gesamtladung Null ist.
Mein Ansatz war jetzt:
 \ \ \ mit \ \ \ r^2 E_r=q\exp(-\alpha r)) komme ich dann auf = -\frac{\alpha q}{r^2}exp(-\alpha r) )
Stimmt das soweit? Für die zwei wollte ich dann über den gesamten Raum integrieren. Die Integrale über die Winkel liefern mir 4pi, die heben sich dann schön mit denen aus der Divergenzgleichung raus, so dass sich mein Problem auf  ) ändert. Das sollte Null ergeben. Nur habe ich keine Idee, wie ich auf eine Stammfunktion von dem Teil kommen soll.
Kann mir da jemand weiterhelfen?
_________________
Nikolas, the mod formerly known as Toxman.
Erwarte das Beste und sei auf das Schlimmste vorbereitet. |
|
 |
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 13. Nov 2006 17:54 Titel: |
|
|
Ich habe das ehrlich gesagt noch nicht genau nachgerechnet, aber vielleicht helfen dir auf die Schnelle schon diese Ideen:
1) Kann es sein, dass du dich im Nenner um den Faktor r vertan hast ?
fälschlicherweise als Einheitsvektor in r-Richtung interpretiert hast. Vielmehr hat 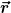 die Länge r und nicht 1, und
2) Hast du beim Integrieren in Kugelkoordinaten berücksichtigt, dass das Volumenelement in Kugelkoordinaten noch den Faktor r^2 enthält ? Kann es sein, dass die Integrationsgrenzen eher Null und Unendlich sein sollten?
3) Bei fiesen Integralen frage ich gern Mathematica online:
http://integrals.wolfram.com/index.jsp
Dafür, dass dein Integral  keine vernünftige Stammfunktion zu haben scheint, spricht, dass Mathematica zu "abstrusen" Spezialfunktionen wie dem exponentiellen Integral Ei[z] greift, um die Stammfunktion darzustellen. (Wenn man wirklich wissen möchte, was das ist, dann schaut man wohl am besten erstmal direkt bei Mathematica online rein  )
Falls meine Vermutungen mit den Faktoren von r stimmen, ergibt sich allerdings ein viel braveres und integrierbareres Integral  |
|
|
schnudl
Moderator
Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
| schnudl Verfasst am: 13. Nov 2006 18:00 Titel: |
|
|
Wahrscheinlich hilft Dir das nicht weiter, aber ich habe in den wolfram integrator eingeben
1/x^2 Exp[-a x]
und bekomme
....
siehe
http://integrals.wolfram.com/index.jsp
Es ist ein "Ei(x)" exponetial integral drinnen, das ich eigentlich nicht kenne, aber die Funktion hat bei x=infty und x=0 Singularitäten, sodass man nicht einfach einsetzen kann...
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
|
schnudl
Moderator
Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
| schnudl Verfasst am: 13. Nov 2006 18:08 Titel: |
|
|
@dermarkus hat glaube ich Recht: Du brauchst nur von Null bis Unendlich integrieren. Das Problem ist, dass Ei(0) minus unendlich wird, sodass dir das ganze eigentlich nichts nützt - es sei denn du hast eine Reihenentwicklung. Eine solche gibt es für x=0 unter
http://functions.wolfram.com/GammaBetaErf/ExpIntegralEi/06/01/01/
 = \frac{1}{2}(log(z) - log(1/z)) = ...)+... )
Ich knn aber nicht sagen, ob es was nützt...grausliche Singularitäten !
Für z= infty gibt es keine Probleme.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
|
Nikolas
Ehrenmitglied
Anmeldungsdatum: 14.03.2004
Beiträge: 1873
Wohnort: Freiburg im Brsg.
|
| Nikolas Verfasst am: 14. Nov 2006 09:52 Titel: |
|
|
Das r von -infty aus zu integrieren ist natürlich völliger Unsinn. Kugelkoordinaten sind für negative Radien auch nicht sinnvoll definiert.
Wenn ich für \vec{r} den Vektor) einsetze und das Skalarprodukt mit Nabla bilde, komme ich erst mal auf einen recht unschönen langen Ausdruck. In fast allen steht aber ein cos \phi, das ich von 0 bis 2pi integrieren muss, wodurch der ganze Ausdruck stirbt. [Ist das wirklich so? Bei Integralen über verschiedene Variablen darf man das Mehrfachintegral doch einfach auseinander ziehen und als Produkt aus den einzelnen Integralen betrachten. Und sobald dann eines Null ist, brauche ich die anderen nicht mehr zu betrachten.]
der letzte Ausdruck sieht dann so aus:
q\exp(-\alpha)/r^2)
damit komme ich dann auf auf das Raumintegral \sin(\theta)\exp(-\alpha r)*r^2\sin(\theta))
Für r*exp(\alpha r) habe ich mit dem Link aus dem Thread das hier gefunden: ) was man recht schnell nachrechnen kann. Wenn man das aber zwischen Null und infty auswertet komme ich auf 1/alpha^2...
Somit habe ich sicher schon mal ein paar Fehler weniger, aber so ganz richtig sieht das noch nicht aus.
_________________
Nikolas, the mod formerly known as Toxman.
Erwarte das Beste und sei auf das Schlimmste vorbereitet. |
|
|
Bruce
Anmeldungsdatum: 20.07.2004
Beiträge: 537
|
| Bruce Verfasst am: 15. Nov 2006 21:16 Titel: |
|
|
Hallo Physikerboard 
Ich habe mir mal die Mühe gemacht, die Berechnung der Ladungsdichte in
kartesischen Koordinaten durchzuführen. Das scheint mir übersichtlicher
als in sphärischen Polarkoordinaten und sieht im Ergebnis so aus:
}{r^2})\;=\;q\,\frac{\exp(-\alpha r)}{r^2}\,\sum_{i}(1-\frac{x_i^2}{r^2}(2+\alpha r))\;=\;q\frac{\exp(-\alpha r)}{r^2}(1-\alpha r))
Die Gesamtladung ist dann proportional
\frac{\exp(-\alpha r)}{r^2}\,4\pi r^2\,dr\;=\;4\pi q\int_{0}^{\infty}(1-\alpha r)\exp(-\alpha r)\,dr\;=0)
und verschwindet somit.
Dieses Ergebnis erhält man allerdings viel einfacher direkt aus dem
gegebenen E-Feld durch Anwendung des Gauß'schen Satzes.
Falls das gegebene Feld nicht proportional zu r^-1 sondern proportional
zu r^-2 wäre, dann müßte man die Singularität von div E für r=0 genauso
sorgfältig behandeln wie für die Punktladung, d.h. zu der in kartesischen
Koordinaten berechnten Divergenz müßte noch eine Delta-Funktion addiert
werden, um die Felderzeugende Gesamtladung zu erhalten.
Gruß von Bruce |
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 16. Nov 2006 00:07 Titel: |
|
|
@Nikolas:
Mit deiner Berechnung von  bin ich nicht ganz einverstanden:
Wenn ich das ausrechne, dann bekomme ich in Kugelkoordinaten (die  -Komponente von nabla in Kugelkoordinaten ist einfach nur die partielle Ableitung nach ):
 = ... = \left( - \frac{1}{r}-\alpha \right) \cdot \frac{q}{r} e^{-\alpha r})
Hilft dir das weiter? Was bekommst du, wenn du dann die Integration in Kugelkoordinaten ausführst? Kommst du damit auf denselben Ausdruck für das Integral wie Bruce? |
|
|
Bruce
Anmeldungsdatum: 20.07.2004
Beiträge: 537
|
| Bruce Verfasst am: 16. Nov 2006 11:44 Titel: |
|
|
Noch ein kleiner Hinweis, der die Berechnung von div E in
kartesischen Koordinaten für radialsymmetrisches E erleichtert:
\,\vec{r}\,)\;=\;\sum_{i}^{}\frac{\partial}{\partial x_i}(\, x_i \,\phi (r)\, ) \;=\;3\,\phi (r)\,+\,r\frac{d}{dr}\phi (r))
Gruß von Bruce |
|
|
|
Registrieren
Login
FAQ
Suchen
