| Autor |
Nachricht |
Superjochen
Gast
|
 Superjochen Verfasst am: 19. März 2022 13:24 Titel: Energieerhaltung widerlegt? Superjochen Verfasst am: 19. März 2022 13:24 Titel: Energieerhaltung widerlegt? |
 |
|
Meine Frage:
Hallo ihr lieben Physiker,
ich habe eben auf YouTube ein Video gesehen, in dem behauptet wird, dass der Energieerhaltungssatz erwiesenermaßen falsch sei und die Energie zu einem Teil ins Nichts verpufft.Das Video selbst kann ich leider nicht als Gast posten, heißt aber: "Warum Energie doch zerstörbar ist".
Meine Ideen:
Ich selbst habe eigentlich gedacht, dass man den Energieerhaltungssatz gar nicht auf das Universum anwenden kann, da Energie so in der ART nicht voll definiert ist. Stimmt das so noch, mit der Konsequenz, dass das Video Blödsinn ist oder ist mein letzter Stand zu dem Thema lang überholt?
Danke für eure Mithilfe! |
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 19. März 2022 13:58 Titel: Nils Hoppenstedt Verfasst am: 19. März 2022 13:58 Titel: |
 |
|
Ja, die Darstellung im Video ist im Wesentlichen korrekt. Die Energieerhaltung basiert auf der Homogenität der Zeit (wenn es also egal ist, ob ich ein Experiment jetzt durchführe oder einen Tag später - vorausgesetzt, dass sich ansonsten nichts ändert). Diese Voraussetzung ist für Raumbereiche, die klein im Vergleich zum Universum sind gut erfüllt, aber nicht für das Universum als Ganzes, da erstens das Universum wegen seiner Expansion eine zeitabhängige Metrik besitzt und zweitens durch den Urknall ein Ereignis explizit ausgezeichnet ist. Es gibt also keine Gesamtenergie des Universums im Sinne einer Erhaltungsgröße.
Viele Grüße,
Nils
_________________
Ihr da Ohm macht doch Watt ihr Volt! |
|
 |
Superjochen
Gast
|
 Superjochen Verfasst am: 19. März 2022 14:16 Titel: Superjochen Verfasst am: 19. März 2022 14:16 Titel: |
 |
|
|
Vielen Dank Nils, deine Erklärung ist aber wesentlich besser als die im Video. Denn dort wird ja behauptet, dass das Universum Energie verliert, während du einfach sagst, dass die Energieerhaltung für das Universum nicht definiert ist. Das ist schon ein Unterschied. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 19. März 2022 14:31 Titel: index_razor Verfasst am: 19. März 2022 14:31 Titel: |
 |
|
| Superjochen hat Folgendes geschrieben: | | Vielen Dank Nils, deine Erklärung ist aber wesentlich besser als die im Video. Denn dort wird ja behauptet, dass das Universum Energie verliert, während du einfach sagst, dass die Energieerhaltung für das Universum nicht definiert ist. Das ist schon ein Unterschied. |
Aus den Friedmann-Gleichungen folgt aber für die Energiedichte 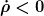 im expandierenden Universum. Also gilt für die Energie ein lokaler "Nichterhaltungssatz" mit negativer Quellendichte. Deshalb ist es schon sinnvoll zu sagen, daß Energie verschwindet. im expandierenden Universum. Also gilt für die Energie ein lokaler "Nichterhaltungssatz" mit negativer Quellendichte. Deshalb ist es schon sinnvoll zu sagen, daß Energie verschwindet.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
 |
Superjochen
Gast
|
 Superjochen Verfasst am: 19. März 2022 14:41 Titel: Superjochen Verfasst am: 19. März 2022 14:41 Titel: |
 |
|
|
Aber dann kann man global nicht sagen, wohin diese geht? Irgendwie verstehe ich es nicht. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 19. März 2022 14:49 Titel: index_razor Verfasst am: 19. März 2022 14:49 Titel: |
 |
|
Sie geht nirgendwo hin, sie verschwindet einfach. Für mich bedeutet das genau, daß die Energie nicht erhalten ist. Wenn sie irgendwohin ginge (z.B. in das Gravitationsfeld), dann würde man dieses "Irgendwo" einfach als weitere Energieform definieren und hätte wieder einen Erhaltungssatz für die Energie. Das Gravitationsfeld scheidet übrigens aus, weil man ihm keine lokale Energiedichte zuschreiben kann, so daß 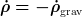 . .
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
 |
Superjochen
Gast
|
 Superjochen Verfasst am: 19. März 2022 15:18 Titel: Superjochen Verfasst am: 19. März 2022 15:18 Titel: |
 |
|
Ok, heißt das jetzt im Umkehrschluss, dass der Energieerhaltungssatz für das Universum global betrachtet widerlegt oder nicht definiert ist?
So wie ich es bisher verstanden habe, ist er auf Grund der Gravitation nicht definiert...aber ich habe davon ja auch keine Ahnung. |
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 19. März 2022 16:58 Titel: Nils Hoppenstedt Verfasst am: 19. März 2022 16:58 Titel: |
 |
|
Wie gesagt, es gibt keine Gesamtenergie des Universums im Sinne einer Erhaltungsgröße. "Widerlegt" wurde da nichts, da ja auch nichts gegenteiliges behauptet wurde. Die Erhaltungssätze in der Physik gelten halt nur, wenn gewisse Symmetrien vorliegen. Und wenn diese nicht vorliegen, ist die entsprechende Größe eben nicht erhalten (oder lässt sich erst gar nicht definieren). Das wissen wir seit 1918 als Emmy Noether das nach ihr benannte Theorem formuliert hat (wie auch im Video erwähnt).
Viele Grüße,
Nils
_________________
Ihr da Ohm macht doch Watt ihr Volt! |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 19. März 2022 17:25 Titel: index_razor Verfasst am: 19. März 2022 17:25 Titel: |
 |
|
| Superjochen hat Folgendes geschrieben: | Ok, heißt das jetzt im Umkehrschluss, dass der Energieerhaltungssatz für das Universum global betrachtet widerlegt oder nicht definiert ist?
|
Ich würde einfach sagen, daß die Energie nicht lokal erhalten ist, d.h. daß in der Bilanzgleichung für Energiedichte (und -stromdichte) ein nichtverschwindender Quellenterm vorkommt. Etwas anderes muß es, denke ich, nicht heißen.
Ob die Gesamtenergie, also das Integral über die Energiedichte, existiert, ist m.E. eine davon unabhängige Frage. Denn wie auch immer man die Gesamtenergie definiert, wenn in einem homogenen Universum an jedem Punkt die Energiedichte abnimmt, dann muß auch jede sinnvoll definierte Gesamtenergie abnehmen.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
 |
Ich
Anmeldungsdatum: 11.05.2006
Beiträge: 913
Wohnort: Mintraching
|
 Ich Verfasst am: 19. März 2022 17:31 Titel: Ich Verfasst am: 19. März 2022 17:31 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | Aus den Friedmann-Gleichungen folgt aber für die Energiedichte 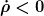 im expandierenden Universum. Also gilt für die Energie ein lokaler "Nichterhaltungssatz" mit negativer Quellendichte. Deshalb ist es schon sinnvoll zu sagen, daß Energie verschwindet. im expandierenden Universum. Also gilt für die Energie ein lokaler "Nichterhaltungssatz" mit negativer Quellendichte. Deshalb ist es schon sinnvoll zu sagen, daß Energie verschwindet. |
...was aber an der zeitabhängigen Metrik liegt, in der Impulse mit 1/a skalieren. In einer solchen Metrik "verschwindet" auch in flacher Raumzeit Energie, ganz ohne Gravitation. Solche koordinatenabhängigen Größen sind Definitionssache, und damit auch die Aussage, ob Energie verschwindet oder nicht. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 19. März 2022 17:39 Titel: index_razor Verfasst am: 19. März 2022 17:39 Titel: |
 |
|
| Ich hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | Aus den Friedmann-Gleichungen folgt aber für die Energiedichte 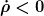 im expandierenden Universum. Also gilt für die Energie ein lokaler "Nichterhaltungssatz" mit negativer Quellendichte. Deshalb ist es schon sinnvoll zu sagen, daß Energie verschwindet. im expandierenden Universum. Also gilt für die Energie ein lokaler "Nichterhaltungssatz" mit negativer Quellendichte. Deshalb ist es schon sinnvoll zu sagen, daß Energie verschwindet. |
...was aber an der zeitabhängigen Metrik liegt, in der Impulse mit 1/a skalieren. In einer solchen Metrik "verschwindet" auch in flacher Raumzeit Energie, ganz ohne Gravitation. Solche koordinatenabhängigen Größen sind Definitionssache, und damit auch die Aussage, ob Energie verschwindet oder nicht. |
Ich weiß. Die Frage, ob die Energie lokal erhalten ist, setzt, denke ich, immer eine gewisse ausgezeichnete Klasse von Beobachtern voraus, bzgl. deren man die Bilanzgleichung 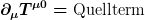 untersucht. Das Ergebnis ist nicht unabhängig davon, wie sich die Vierergeschwindigkeiten dieser Beobachter selbst mit der Zeit ändern. untersucht. Das Ergebnis ist nicht unabhängig davon, wie sich die Vierergeschwindigkeiten dieser Beobachter selbst mit der Zeit ändern.
In einer statischen Raumzeit ist so eine Klasse von Beobachtern durch die zeitartigen Killingfelder gegeben. (Und bzgl. dieser Beobachter verschwindet keine Energie.) Im Robertson-Walker-Universum gibt es zwar keine solchen Killingfelder. Es gibt aber trotzdem eine ausgezeichnete Klasse von Beobachtern, nämlich die, für die das Universum homogen und isotrop ist. Deswegen halte ich es trotzdem für sinnvoll zu behaupten, daß die Gesamtenergie im expandierenden Robertson-Walker-Universum abnimmt. (Auf diese Beobachter habe ich auch meine Bilanzgleichung bezogen, d.h. <0) etc.) etc.)
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt
Zuletzt bearbeitet von index_razor am 19. März 2022 18:03, insgesamt einmal bearbeitet |
|
 |
Superjochen
Gast
|
 Superjochen Verfasst am: 19. März 2022 17:58 Titel: Superjochen Verfasst am: 19. März 2022 17:58 Titel: |
 |
|
Danke für eure Erklärungen. Ic denke, ich kann Ihnen halbwegs folgen. Meine Frage mit der Gesamtenergie stellte ich, da sowohl in Wikipedia als auch hier im Forum stand (glaube in Beiträgen des Mods TomS), das die gesamte Energie nicht definierbar ist.
Hat die lokale Energieabnahme eigentlich irgendwelche praktischen Konsequenzen? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 19. März 2022 18:06 Titel: TomS Verfasst am: 19. März 2022 18:06 Titel: |
 |
|
Zumindest kannst du in einem flachen FRW-Universum mit
 = \text{const})
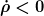
eine Energie
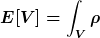
definieren.
Die Frage ist nur, wie du das Volumen V definierst.
Wenn du zum Beispiel das Volumen auf der Gleichzeitigkeitshyperfläche eines mitbewegten Beobachters durch ihrerseits mitbewegte Beobachter auf einer Kugelschale um den Beobachter definierst, dann wird dieses Volumen zunehmen, während die Energiedichte abnimmt.
Wie trennst du diese Effekte? Wie legst du allgemein das Volumen physikalisch fest?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Ich
Anmeldungsdatum: 11.05.2006
Beiträge: 913
Wohnort: Mintraching
|
 Ich Verfasst am: 19. März 2022 18:17 Titel: Ich Verfasst am: 19. März 2022 18:17 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | Es gibt aber trotzdem eine ausgezeichnete Klasse von Beobachtern, nämlich die, für die das Universum homogen und isotrop ist. Deswegen halte ich es trotzdem für sinnvoll zu behaupten, daß die Gesamtenergie im expandierenden Robertson-Walker-Universum abnimmt. (Auf diese Beobachter habe ich auch meine Bilanzgleichung bezogen, d.h. <0) etc.) etc.) |
Du hast eigentlich von einer lokalen Energiedichte gesprochen, und da gehe ich gerne mit, dass die im Friedmann-Universum kleiner wird. Ich hielt nur die Aussage, dass die Energie einfach "verschwindet" für zu stark, weil sie wie gesagt koordinatenabhängig ist. Man kann z.B. in jeder Umgebung Normalkoordinaten einführen, in denen wiederum nichts verschwindet. Und Normalkoordinaten sind m.E. durchaus auch in gewissem Sinne kanonisch, weil sie in jeder Rauzeit Koordinatenartefakte so weit wie möglich eliminieren.
Bei der globalen Energie wäre ich von Haus aus noch vorsichtiger mit starken Aussagen, da ist alles noch schwammiger.
Zuletzt bearbeitet von Ich am 19. März 2022 18:32, insgesamt einmal bearbeitet |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 19. März 2022 18:25 Titel: index_razor Verfasst am: 19. März 2022 18:25 Titel: |
 |
|
| Superjochen hat Folgendes geschrieben: | Danke für eure Erklärungen. Ic denke, ich kann Ihnen halbwegs folgen. Meine Frage mit der Gesamtenergie stellte ich, da sowohl in Wikipedia als auch hier im Forum stand (glaube in Beiträgen des Mods TomS), das die gesamte Energie nicht definierbar ist.
Hat die lokale Energieabnahme eigentlich irgendwelche praktischen Konsequenzen? |
Es stimmt, daß sich im allgemeinen keine Gesamtenergie definieren läßt. Das trifft wohl auch auf unser Universum zu. Die Sache wird auch noch dadurch komplizierter, daß man das Gravitationsfeld nicht einfach aus der Bilanz entfernen kann, obwohl man ihm nicht mal eine Energiedichte zuordnen kann. (Ein schwarzes Loch hat z.B. eine Masse und damit eine Energie, obwohl es sich um eine Vakuumlösung handelt, also überall in der Schwarzschildraumzeit die Energiedichte verschwindet.)
Im allgemeinen ist die Definition einer Gesamtenergie nur sinnvoll, wenn die Raumzeit im Unendlichen frei von Materie ist. Wenn einfach überall Materie ist, geht das nicht. In gewisser Weise ist es nun natürlich auch sinnlos zu behaupten, eine nicht definierte Größe würde mit der Zeit abnehmen. Aber das bedeutet eben noch nicht, daß gar keine weiteren sinnvollen Aussagen mehr möglich sind. Wie gesagt, haben wir es ja mit einem homogenen, isotropen Universum zu tun. Das heißt es gibt zumindest Beobachter, die lokal beurteilen können, wie sich die Energiedichte der Materie und Strahlung ändert und dabei ausschließen können, daß dies z.B. lediglich an ihrer eigenen Bewegung relativ zur Hintergrundstrahlung liegt. Wenn jeder dieser Beobachter feststellt, daß in seiner Umgebung die Summe aus Materie- und Strahlunsgenergie abnimmt, dann ist das eine sinnvolle Aussage über das gesamte Universum, die man m.E. mit gutem Recht als Abnahme seiner Gesamtenergie bezeichnen kann.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt
Zuletzt bearbeitet von index_razor am 19. März 2022 21:47, insgesamt einmal bearbeitet |
|
 |
Ich
Anmeldungsdatum: 11.05.2006
Beiträge: 913
Wohnort: Mintraching
|
 Ich Verfasst am: 19. März 2022 18:32 Titel: Ich Verfasst am: 19. März 2022 18:32 Titel: |
 |
|
| Superjochen hat Folgendes geschrieben: | | Hat die lokale Energieabnahme eigentlich irgendwelche praktischen Konsequenzen? |
Es hilft zum Beispiel, dass die Hintergrundstrahlung nur mehr 2,7 K heiß ist, nicht 3000 K. Aber nicht überbewerten: diese Abnahme der lokalen Energiedichte ist tatsächlich kein lokaler Effekt, sondern beruht darauf, dass diese Strahlung von weit her kommrt aus Regionen, die relativ zu uns bewegt sind.
Wenn man "lokal" im engen Sinne nimmt, merkt man nichts davon. Man würde nie expandierende Koordinaten hernehmen, um lokale Physik zu beschreiben. also gilt da auch die Energieerhaltung. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 19. März 2022 18:51 Titel: index_razor Verfasst am: 19. März 2022 18:51 Titel: |
 |
|
| Ich hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | Es gibt aber trotzdem eine ausgezeichnete Klasse von Beobachtern, nämlich die, für die das Universum homogen und isotrop ist. Deswegen halte ich es trotzdem für sinnvoll zu behaupten, daß die Gesamtenergie im expandierenden Robertson-Walker-Universum abnimmt. (Auf diese Beobachter habe ich auch meine Bilanzgleichung bezogen, d.h. <0) etc.) etc.) |
Du hast eigentlich von einer lokalen Energiedichte gesprochen, un da gehe ich gerne mit, dass die im Friedmann-Universum kleiner wird.
|
Wieso "eigentlich"? Ich spreche immer noch von einer Energiedichte, genauer gesagt von der Energiedichte von Materie und Strahlung.
| Zitat: |
Ich hielt nur die Aussage, dass die Energie einfach "verschwindet" für zu stark, weil sie wie gesagt koordinatenabhängig ist. Man kann z.B. in jeder Umgebung Normalkoordinaten einführen, in denen wiederum nichts verschwindet. |
Das kannst du aber auch in Normalkoordinaten nur in einem einzigen Ereignis garantieren (oder wegen der Homogenität womöglich auch an verschiedenen Orten zu fester Zeit), aber nicht in der ganzen Umgebung. In dieser gilt folglich auch die Gl. 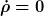 nicht überall. (Ansonsten müßte in der ganzen Umgebung die Raumzeit flach sein.) Sicher gibt es Koordinaten, in denen nicht überall. (Ansonsten müßte in der ganzen Umgebung die Raumzeit flach sein.) Sicher gibt es Koordinaten, in denen 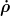 auch mal positiv sein kann. (Auch wenn dies höchstwahrscheinlich keine Normalkoordinaten sein werden.) Aber wie gesagt, Voraussetzung meiner Behauptung war ohnehin die Homogenität. Ich setze also Beobachter voraus, für die auch mal positiv sein kann. (Auch wenn dies höchstwahrscheinlich keine Normalkoordinaten sein werden.) Aber wie gesagt, Voraussetzung meiner Behauptung war ohnehin die Homogenität. Ich setze also Beobachter voraus, für die 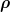 räumlich konstant ist. (Ansonsten müßte ich ohnehin noch die Energiestromdichte mit in die Bilanzgleichung aufnehmen.) räumlich konstant ist. (Ansonsten müßte ich ohnehin noch die Energiestromdichte mit in die Bilanzgleichung aufnehmen.)
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
 |
Ich
Anmeldungsdatum: 11.05.2006
Beiträge: 913
Wohnort: Mintraching
|
 Ich Verfasst am: 19. März 2022 23:23 Titel: Ich Verfasst am: 19. März 2022 23:23 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Wieso "eigentlich"? Ich spreche immer noch von einer Energiedichte, genauer gesagt von der Energiedichte von Materie und Strahlung. |
Weil du später, im zitierten Beitrag, von einer Gesamtenergie gesprochen hast. Die finde ich noch deutlich schwieriger.
| Zitat: |
| Ich hat Folgendes geschrieben: |
Ich hielt nur die Aussage, dass die Energie einfach "verschwindet" für zu stark, weil sie wie gesagt koordinatenabhängig ist. Man kann z.B. in jeder Umgebung Normalkoordinaten einführen, in denen wiederum nichts verschwindet. |
Das kannst du aber auch in Normalkoordinaten nur in einem einzigen Ereignis garantieren (oder wegen der Homogenität womöglich auch an verschiedenen Orten zu fester Zeit), aber nicht in der ganzen Umgebung. In dieser gilt folglich auch die Gl. 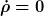 nicht überall. nicht überall. |
In Normalkoordinaten ist das Universum nicht homogen.
Energieerghaltung gilt natürlich nie exakt, weil die ART eben keine Gravitationsenergie kennt. Aber der Term ) verschwindet. Und wenn man ein Gravitationspotential eiführt (was man in diesen quasistatischen Koordinaten ja kann), dann hat man in ich weiß nicht wievielter Näherung die Energie erhalten. verschwindet. Und wenn man ein Gravitationspotential eiführt (was man in diesen quasistatischen Koordinaten ja kann), dann hat man in ich weiß nicht wievielter Näherung die Energie erhalten.
| Zitat: | Ich setze also Beobachter voraus, für die 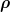 räumlich konstant ist. (Ansonsten müßte ich ohnehin noch die Energiestromdichte mit in die Bilanzgleichung aufnehmen.) räumlich konstant ist. (Ansonsten müßte ich ohnehin noch die Energiestromdichte mit in die Bilanzgleichung aufnehmen.) |
Kannst du ja machen, und wenn du ein Koordinatensystem einführst, in dem diese Beobachter ruhen (obwohl sie sich de facto auseinanderbewegen), dann ist die Energie in der von dir beschriebenen Weise nicht erhalten. Wenn du andere Koordinaten einführst, gilt das aber nicht. Deswegen ist die Aussage, dass Energie einfach verschwindet, für mich ja auch nicht falsch. Aber zu stark, weil sie sich nach physikalischem Faktum, also invarianter Tatsache, anhört. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 20. März 2022 10:11 Titel: TomS Verfasst am: 20. März 2022 10:11 Titel: |
 |
|
Siehe oben. Mich würde interessieren, wie du ein endliches Volumen physikalisch sinnvoll definierst.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Ich
Anmeldungsdatum: 11.05.2006
Beiträge: 913
Wohnort: Mintraching
|
 Ich Verfasst am: 20. März 2022 10:57 Titel: Ich Verfasst am: 20. März 2022 10:57 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Siehe oben. Mich würde interessieren, wie du ein endliches Volumen physikalisch sinnvoll definierst. |
Das ist für die Energiedichte eigentlich egal. Wenn man ein "repräsentatives Stück Universum" haben will, dann sollten die Grenzen mitbewegt sein. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 20. März 2022 11:20 Titel: index_razor Verfasst am: 20. März 2022 11:20 Titel: |
 |
|
| Ich hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Wieso "eigentlich"? Ich spreche immer noch von einer Energiedichte, genauer gesagt von der Energiedichte von Materie und Strahlung. |
Weil du später, im zitierten Beitrag, von einer Gesamtenergie gesprochen hast. Die finde ich noch deutlich schwieriger.
|
Ich auch, deswegen habe ich es ja danach auch etwas ausführlicher erklärt ohne, daß sich m.E. an der Schlußfolgerung viel ändert.
| Zitat: |
| Zitat: |
| Ich hat Folgendes geschrieben: |
Ich hielt nur die Aussage, dass die Energie einfach "verschwindet" für zu stark, weil sie wie gesagt koordinatenabhängig ist. Man kann z.B. in jeder Umgebung Normalkoordinaten einführen, in denen wiederum nichts verschwindet. |
Das kannst du aber auch in Normalkoordinaten nur in einem einzigen Ereignis garantieren (oder wegen der Homogenität womöglich auch an verschiedenen Orten zu fester Zeit), aber nicht in der ganzen Umgebung. In dieser gilt folglich auch die Gl. 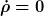 nicht überall. nicht überall. |
In Normalkoordinaten ist das Universum nicht homogen. Energieerghaltung gilt natürlich nie exakt, weil die ART eben keine Gravitationsenergie kennt. Aber der Term ) verschwindet. verschwindet.
|
Ich denke du hast meinen Einwand mißverstanden. Mit der Homogenität wollte ich dir sogar noch entgegen kommen. Ansonsten verschwindet 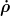 höchstens in einem Ereignis. Das macht noch keinen lokalen Erhaltungssatz. höchstens in einem Ereignis. Das macht noch keinen lokalen Erhaltungssatz.
Ich denke mit der Homogenität kann man zumindest erreichen, daß 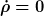 überall zu einem Zeitpunkt. Das reicht aber immer noch nicht. überall zu einem Zeitpunkt. Das reicht aber immer noch nicht.
| Zitat: |
Und wenn man ein Gravitationspotential eiführt (was man in diesen quasistatischen Koordinaten ja kann), dann hat man in ich weiß nicht wievielter Näherung die Energie erhalten.
|
In erster Näherung, d.h. bis auf Vernachlässigung von Krümmungstermen. Mehr können auch Normalkoordinaten natürlich nicht liefern. Das ist genau was ich schreibe. Aber das ist natürlich äquivalent zur Aussage, daß die Energie ab zweiter Ordnung nicht mehr erhalten ist, was wiederum nur eine präzisere Formulierung der Tatsache ist, daß kein lokaler Erhaltungssatz gilt. Ein lokaler Erhaltungssatz besagt, daß
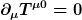
an jedem Ort zu jeder Zeit gilt, nicht nur in einem Ereignis oder zu einem Zeitpunkt.
| Zitat: |
| Zitat: | Ich setze also Beobachter voraus, für die 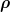 räumlich konstant ist. (Ansonsten müßte ich ohnehin noch die Energiestromdichte mit in die Bilanzgleichung aufnehmen.) räumlich konstant ist. (Ansonsten müßte ich ohnehin noch die Energiestromdichte mit in die Bilanzgleichung aufnehmen.) |
Kannst du ja machen, und wenn du ein Koordinatensystem einführst, in dem diese Beobachter ruhen (obwohl sie sich de facto auseinanderbewegen), dann ist die Energie in der von dir beschriebenen Weise nicht erhalten.
|
Ich führe ein Koordinatensystem ein, in dem das Universum homogen erscheint, was es de facto ist. Dann verschwinden alle räumlichen Ableitungen in der Bilanzgleichung
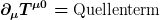
und übrig bleibt
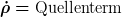
Aus der Friedmanngleichung folgere ich dann, daß der Quellterm negativ ist. Folglich nimmt die räumlich konstante Energiedichte überall ab. Auch wenn ich also keine Gesamtenergie mathematisch definieren kann, ist es sinnvoll zu behaupten, daß Energie verschwindet.
| Zitat: |
Wenn du andere Koordinaten einführst, gilt das aber nicht. Deswegen ist die Aussage, dass Energie einfach verschwindet, für mich ja auch nicht falsch. Aber zu stark, weil sie sich nach physikalischem Faktum, also invarianter Tatsache, anhört. |
Es ist ein physikalisches Faktum, genauso wie die Homogenität des Robertson-Walker-Universum oder die Tatsache, daß z.B. der Minkowskiraum oder die Schwarzschildmetrik statisch sind, physikalische Fakten sind. Andere Koordinaten können diese Tatsachen nur verschleiern, aber nichts an ihnen ändern.
Wenn wir von der lokalen Energiebilanz in irgendeiner dieser Raumzeiten reden wollen, verwenden wir immer Koordinaten, die an ihre Symmetrien angepaßt sind. Darauf hast du oben selbst hingeweisen. Ansonsten können wir auch im Minkowskiraum plötzlich die Energiebilanzgleichung verletzen. Die Symmetrien des Robertson-Walker-Universums zeichnen eine Klasse von "mitbewegten" Beobachtern aus. Ich wähle also nicht einfach irgendein Koordinatensystem, sondern eines, dessen Zeitachse durch die Vierergeschwindigkeiten 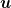 dieser Beobachter gegeben ist. Dadurch ist meine Aussage weniger willkürlich, als du sie darstellst. Natürlich ändert sich der Quellterm, wenn ich dieser Beobachter gegeben ist. Dadurch ist meine Aussage weniger willkürlich, als du sie darstellst. Natürlich ändert sich der Quellterm, wenn ich 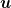 ändere, wie in statischen Raumzeiten auch. Er kann aber niemals überall verschwinden oder überall nicht-negativ sein (letzteres vermute ich jedenfalls, habe ich aber nicht bewiesen, aber daß er nicht überall null sein kann ist klar). Das einzige was er überall sein kann, ist negativ. Deswegen halte ich es durchaus für sinnvoll zu sagen, daß die Energie im expandierenden homogenen Universum verschwindet. ändere, wie in statischen Raumzeiten auch. Er kann aber niemals überall verschwinden oder überall nicht-negativ sein (letzteres vermute ich jedenfalls, habe ich aber nicht bewiesen, aber daß er nicht überall null sein kann ist klar). Das einzige was er überall sein kann, ist negativ. Deswegen halte ich es durchaus für sinnvoll zu sagen, daß die Energie im expandierenden homogenen Universum verschwindet.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 20. März 2022 11:25 Titel: TomS Verfasst am: 20. März 2022 11:25 Titel: |
 |
|
| Ich hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Siehe oben. Mich würde interessieren, wie du ein endliches Volumen physikalisch sinnvoll definierst. |
Das ist für die Energiedichte eigentlich egal. |
s.o. - es geht um die Energie.
| Ich hat Folgendes geschrieben: | | Wenn man ein "repräsentatives Stück Universum" haben will, dann sollten die Grenzen mitbewegt sein. |
s.o. - habe ich so angesetzt.
Dann ist die erste Frage, ob die so definierte Größe eine Energie mit geeigneten Transformationseigenschaften d.h. die Null-Komponente eines Vierervektors ist. Und die zweite Frage ist, wie man die Effekte eines expandierenden Volumens von der abnehmenden Energiedichte trennt (das o.g. expandierende Volumen ist z.B. thermodynamisch nicht abgeschlossen).
(wieder zunächst speziell für ein flaches, dann für ein nicht-flaches und zuletzt für ein inhomogenes, jeweils expandieres Universum).
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 21. März 2022 21:13 Titel: index_razor Verfasst am: 21. März 2022 21:13 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Und die zweite Frage ist, wie man die Effekte eines expandierenden Volumens von der abnehmenden Energiedichte trennt |
Wenn die Gesamtenergie ) im Volumen im Volumen ) zur späteren Zeit kleiner ist, als zur früheren Zeit, gibt es nur zwei Möglichkeiten. Entweder gab es in der Zwischenzeit einen Energiestrom aus dem Volumen V(t) heraus oder Energie ist verschwunden. Aus dem mitbewegten Volumen strömt aber nichts heraus (die Energiestromdichte ist überall null). Also muß (aus Sicht der mitbewegten Beobachter) Energie verschwunden sein. zur späteren Zeit kleiner ist, als zur früheren Zeit, gibt es nur zwei Möglichkeiten. Entweder gab es in der Zwischenzeit einen Energiestrom aus dem Volumen V(t) heraus oder Energie ist verschwunden. Aus dem mitbewegten Volumen strömt aber nichts heraus (die Energiestromdichte ist überall null). Also muß (aus Sicht der mitbewegten Beobachter) Energie verschwunden sein.
Man kann es auch so sehen: das mitbewegte Volumen skaliert mit ) , die Energiedichte von Strahlung aber z.B. mit , die Energiedichte von Strahlung aber z.B. mit ) . Also enthält das spätere Volumen nur noch den Anteil . Also enthält das spätere Volumen nur noch den Anteil /a(t_1)) der ursprünglich vorhandenen Strahlungsenergie, obwohl nichts davon aus dem Volumen geströmt ist. der ursprünglich vorhandenen Strahlungsenergie, obwohl nichts davon aus dem Volumen geströmt ist.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 22. März 2022 14:21 Titel: TomS Verfasst am: 22. März 2022 14:21 Titel: |
 |
|
Danke.
Für das homogene und isotrope Universum und für mitbewegte Beobachter ist das sicher sinnvoll. Ich habe nur immer Bauchschmerzen, da es sich eben um eine koordinaten- und beobachterabhängige Aussage geht, durchchecken nicht vernünftig verallgemeinern kann.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Ich
Anmeldungsdatum: 11.05.2006
Beiträge: 913
Wohnort: Mintraching
|
 Ich Verfasst am: 22. März 2022 21:16 Titel: Ich Verfasst am: 22. März 2022 21:16 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | Man kann es auch so sehen: das mitbewegte Volumen skaliert mit ) , die Energiedichte von Strahlung aber z.B. mit , die Energiedichte von Strahlung aber z.B. mit ) . Also enthält das spätere Volumen nur noch den Anteil . Also enthält das spätere Volumen nur noch den Anteil /a(t_1)) der ursprünglich vorhandenen Strahlungsenergie, obwohl nichts davon aus dem Volumen geströmt ist. der ursprünglich vorhandenen Strahlungsenergie, obwohl nichts davon aus dem Volumen geströmt ist. |
Weil ich mich vorher falsch ausgedrückt hatte, steige hier mit einem Beispiel ein, das klar macht, worauf ich mit den Normalkoordinaten hinauswill.
Wir nehmen mal vereinfacht als Beispiel zwei mitbewegte Punkte mit Abstand 2dx (zur Zeit 0). Bei dx ist die Grenze der jeweiligen mitbewegten Volumina. Beide Punkte senden zur Zeit 0 ein Photon (Frequenz f im jeweiligen Ruhesystem) zum anderen Punkt.
In mitbewegten Koordinaten erreichen die Photonen die Grenze nach dt=dx/c und sind je um Hdt*f rotverschoben. Also verlässt netto keine Energie die Volumina, trozdem sinkt die Energiedichte, weil jedes Photon mit der Zeit quasimagisch Energie verliert.
Im Ruhesystem von Punkt 1 hingegen (in nicht expandierenden Koordinaten) sieht die Sache anders aus: Zur Zeit 0 entsteht bei Punkt 1 ein Photon mit Energie f, an Punkt zwei ein um 2dx*f/c rotverschobenes Photon. Nach dt erreichen diese die Grenze, aus Volumen 1 geht ein Photon mit f raus und eins mit f-2dxf/c kommt rein. Deswegen nimmt die Energie in diesem Volumen ab. Nicht, weil sie "verschwindet", sondern weil sie ins Nachbarvolumen rüberströmt.
Der Punkt ist nun, dass das lokal eine gültige und wie gesagt per se kanonische Art ist, den Vorgang zu betrachten. Ob die beiden Punkte teil einer klassische Explosion oder eines expandierenden Universums sind, macht lokal exakt gar keinen Unterschied. Ob lokal Energie verschwindet oder nicht, ist mithin Ansichtssache - wenn man "normale" Koordinaten verwendet, verschwindet auf jeden Fall nichts. Das hat auch nichts damit zu tun, ob das Universum expandiert oder nicht, sondern nur mit den lokal verwendeten Koordinaten.
Also ist die Aussage richtig, dass in mitbewegten Koordinaten Energie verschwindet. Die Aussage, dass in einem expandierenden Universum (ohne expliziten Bezug auf die verwendeten Koordinaten) lokal Energie verschwindet, ist aber zu stark. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 23. März 2022 07:02 Titel: index_razor Verfasst am: 23. März 2022 07:02 Titel: |
 |
|
| Ich hat Folgendes geschrieben: |
Im Ruhesystem von Punkt 1 hingegen (in nicht expandierenden Koordinaten) sieht die Sache anders aus: Zur Zeit 0 entsteht bei Punkt 1 ein Photon mit Energie f, an Punkt zwei ein um 2dx*f/c rotverschobenes Photon. Nach dt erreichen diese die Grenze, aus Volumen 1 geht ein Photon mit f raus und eins mit f-2dxf/c kommt rein. Deswegen nimmt die Energie in diesem Volumen ab. Nicht, weil sie "verschwindet", sondern weil sie ins Nachbarvolumen rüberströmt.
|
Ich habe keine Ahnung, wie du zu dieser Beschreibung kommst. Du behauptest, die Energie zur späteren Zeit sei für Beobachter 1 um genau den Betrag des Energiestroms aus dem Volumen geringer als zur früheren Zeit. Diese Aussage -- ob richtig oder falsch -- hat jedenfalls nicht das geringste mit irgendwelchen Koordinaten zu tun, sondern damit ob das Integral über die Viererdivergenz der Energistromdichte für diesen Beobachter über den definierten Raumzeitbereich verschwindet, d.h.
\sqrt{g}\dd^4 x = 0.)
Das ist eine koordinatenunabhängige Größe. Die Energiestromdichte 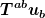 hängt zwar vom Beobachter ab, aber das ist nicht der Punkt. Die Frage ist, ob es einen Beobachter gibt, für den diese Divergenz verschwindet. Das hast du für das Robertson-Walker-Universum nicht gezeigt und ich denke auch nicht, daß es stimmen kann. hängt zwar vom Beobachter ab, aber das ist nicht der Punkt. Die Frage ist, ob es einen Beobachter gibt, für den diese Divergenz verschwindet. Das hast du für das Robertson-Walker-Universum nicht gezeigt und ich denke auch nicht, daß es stimmen kann.
| Zitat: |
Der Punkt ist nun, dass das lokal eine gültige und wie gesagt per se kanonische Art ist, den Vorgang zu betrachten. Ob die beiden Punkte teil einer klassische Explosion oder eines expandierenden Universums sind, macht lokal exakt gar keinen Unterschied. Ob lokal Energie verschwindet oder nicht, ist mithin Ansichtssache - wenn man "normale" Koordinaten verwendet, verschwindet auf jeden Fall nichts. Das hat auch nichts damit zu tun, ob das Universum expandiert oder nicht, sondern nur mit den lokal verwendeten Koordinaten.
|
Nein, das ist falsch, besonders die letzten beiden Behauptungen. Ob lokal Energie verschwindet, hat absolut mit der Frage zu tun ob das Universum expandiert und überhaupt nichts mit der Wahl der Koordinaten.
Allgemeiner hat es mit der völlig koordinatenunabhängigen Frage zu tun ob auf der Raumzeit ein zeitartiges Killingfeld 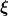 existiert, m.a.W. ob die Raumzeit statisch ist. Dann (und nur dann?) ist der lokale Strom existiert, m.a.W. ob die Raumzeit statisch ist. Dann (und nur dann?) ist der lokale Strom 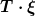 erhalten, es gilt also exakt erhalten, es gilt also exakt  = 0) bzw. bzw.  = 0) . Im expandierenden Universum gibt es kein solches Feld, also auch keinen zugehörigen erhaltenen Strom. (Ich setze hier voraus, daß die Umkehrung des Noether-Theorems gilt.) Das heißt dann die Quellendichte . Im expandierenden Universum gibt es kein solches Feld, also auch keinen zugehörigen erhaltenen Strom. (Ich setze hier voraus, daß die Umkehrung des Noether-Theorems gilt.) Das heißt dann die Quellendichte ) ist für jeden Beobachter mit Vierergeschwindigkeit u irgendwo ungleich null. Daran ändern auch Normalkoordinaten nichts, weil es eine koordinatenunabhängige Aussage ist. ist für jeden Beobachter mit Vierergeschwindigkeit u irgendwo ungleich null. Daran ändern auch Normalkoordinaten nichts, weil es eine koordinatenunabhängige Aussage ist.
| Zitat: |
Also ist die Aussage richtig, dass in mitbewegten Koordinaten Energie verschwindet. Die Aussage, dass in einem expandierenden Universum (ohne expliziten Bezug auf die verwendeten Koordinaten) lokal Energie verschwindet, ist aber zu stark. |
Ganz und gar nicht. Wie gesagt, dann müßtest du auch die Aussage "Das Universum ist homogen und isotrop" für "zu stark" halten. Die basiert nämlich auf exakt denselben Voraussetzungen. Das tust du aber nicht, nehme ich mal an.
Bezug nehmen muß ich übrgens nur auf Beobachter, nicht auf Koordinaten. Das muß ich aber seit jeher, wenn ich von Energiebilanzen reden will, nicht erst in der ART, sondern schon in der Newtonschen Mechanik. Energieerhaltung bedeutet immer, daß es bestimmte Beobachter gibt, für die sich die Gesamtenergie zu keiner Zeit ändert. Meine koordinatenunabhängige, rein physikalische Behauptung ist, daß es solche Beobachter im Robertson-Walker-Universum nicht gibt. Ich vermute auch, daß für alle frei fallenden Beobachter (die beschleunigten sind ohnehin uninteressant) im Laufe der Zeit Energie verschwindet. Da bin ich mir aber nicht sicher. (Die Aufgabe hier wäre jedenfalls für den Energie-Impulstensor ) so eine Schar von Beobachtern zu definieren, für die die Divergenz von so eine Schar von Beobachtern zu definieren, für die die Divergenz von 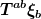 verschwindet oder im Mittel irgendwo nicht-negativ ist.) verschwindet oder im Mittel irgendwo nicht-negativ ist.)
Ich bin mir aber sicher, daß für alle Beobachter, denen das Universum homogen erscheint, die Energie im Laufe der Zeit abnimmt. Das ist ein physikalisches Faktum, und es ist unabhängig von den Koordinaten, die diese Beobachter verwenden.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 23. März 2022 08:47 Titel: TomS Verfasst am: 23. März 2022 08:47 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | [… sondern damit ob das Integral über die Viererdivergenz der Energistromdichte für diesen Beobachter über den definierten Raumzeitbereich verschwindet, d.h.
\sqrt{g}\dd^4 x = 0.)
Das ist eine koordinatenunabhängige Größe. Die Energiestromdichte 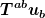 hängt zwar vom Beobachter ab, aber das ist nicht der Punkt. Die Frage ist, ob es einen Beobachter gibt, für den diese Divergenz verschwindet. hängt zwar vom Beobachter ab, aber das ist nicht der Punkt. Die Frage ist, ob es einen Beobachter gibt, für den diese Divergenz verschwindet. |
Das ist sicher ein sinnvoller Ansatz, mir ist aber noch einiges unklar.
u ist ein Vektorfeld, d.h.
 )
und sinnvollerweise
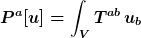
ist abhängig von einer Schar von Beobachtern, nicht nur von einem Beobachter.
Damit sehe ich aber nicht, wie du von der Energie für einen Beobachter sprechen kannst. Ich sehe auch nicht, wie du eine Energieerhaltung oder deren Verletzung für einen Beobachter diskutieren willst, denn was du eigentlich benötigst, ist die Eigenzeit eines Beobachters sowie diesbzgl.
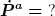
Das hat aber erst mal nichts mit dem von dir genannten Integral zu tun.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 23. März 2022 09:47 Titel: index_razor Verfasst am: 23. März 2022 09:47 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | [… sondern damit ob das Integral über die Viererdivergenz der Energistromdichte für diesen Beobachter über den definierten Raumzeitbereich verschwindet, d.h.
\sqrt{g}\dd^4 x = 0.)
Das ist eine koordinatenunabhängige Größe. Die Energiestromdichte 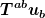 hängt zwar vom Beobachter ab, aber das ist nicht der Punkt. Die Frage ist, ob es einen Beobachter gibt, für den diese Divergenz verschwindet. hängt zwar vom Beobachter ab, aber das ist nicht der Punkt. Die Frage ist, ob es einen Beobachter gibt, für den diese Divergenz verschwindet. |
Das ist sicher ein sinnvoller Ansatz, mir ist aber noch einiges unklar.
u ist ein Vektorfeld, d.h.
 )
und sinnvollerweise
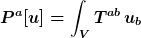
|
Das ist nicht ganz richtig. Das Integral über den Vektor 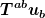 über ein räumliches Volumen ergibt eine Zahl, keinen Vektor. Du mußt (wie bei Flächenintegralen im Dreidimensionalen) den Intergranden mit der Flächennormalen multiplizieren. Das ist in diesem Fall wieder über ein räumliches Volumen ergibt eine Zahl, keinen Vektor. Du mußt (wie bei Flächenintegralen im Dreidimensionalen) den Intergranden mit der Flächennormalen multiplizieren. Das ist in diesem Fall wieder 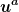 , also ist das Integral , also ist das Integral
}}\dd^3 x = \int_V \rho\sqrt{g^{(3)}}\dd^3 x = E(V))
die eingeschlossenen Energie (aus Sicht des Beobachters u). (Wenn du räumliche Impulse ausrechen willst, mußt du über 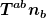 integrieren (wieder mit "Hyperflächenormale" integrieren (wieder mit "Hyperflächenormale" 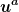 ), wobei nun ebenfalls ), wobei nun ebenfalls 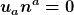 .) .)
| Zitat: |
ist abhängig von einer Schar von Beobachtern, nicht nur von einem Beobachter.
Damit sehe ich aber nicht, wie du von der Energie für einen Beobachter sprechen kannst.
|
Ich muß ja ohnehin voraussetzen, daß für diesen einen Beobachter sowohl zur früheren als auch zur späteren Zeit ein räumliches 3er-Volumen definiert ist, über das er integrieren kann. Alle Ereignisse in diesem Volumen finden für ihn zu einer festen Eigenzeit statt. (Ansonsten handelt es sich aus seiner Sicht nicht um ein "Raumintegral".) Die Vektoren 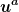 sind dann einfach die Normalenvektoren zu diesem Volumen. Auf der Mantelfläche liegen sind dann einfach die Normalenvektoren zu diesem Volumen. Auf der Mantelfläche liegen 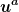 tangential und ihr Verlauf definiert auf invariante Weise die "Zeitabhängigkeit" des räumlichen Volumens. tangential und ihr Verlauf definiert auf invariante Weise die "Zeitabhängigkeit" des räumlichen Volumens.
Insgesamt läuft es immer darauf hinaus, daß ich ein Vierervolumen habe, über dessen Inneres ich (skalare) Divergenzen oder über dessen Rand ich vektorielle Stromdichten integriere. (Laut dem Satz von Gauß jeweils mit demselben koordinatenunabhängigen Ergebnis.)
| Zitat: |
Ich sehe auch nicht, wie du eine Energieerhaltung oder deren Verletzung für einen Beobachter diskutieren willst, denn was du eigentlich benötigst, ist die Eigenzeit eines Beobachters sowie diesbzgl.
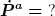
Das hat aber erst mal nichts mit dem von dir genannten Integral zu tun. |
Doch, du mußt nur V nach der Eigenzeit dieses Beobachters parametrisieren und berücksichtigen, daß bei beliebiger Abhängigkeit V(t) auch Energieströme 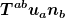 durch durch ) zur Bilanz beitragen. Der Vektor n ist hier normal zur "Mantelfläche" des Vierervolumens, über dessen gesamten Rand integriert wird. Wenn die Energie erhalten ist, verschwindet das komplette Randintegral unabhängig von t. Also ist die Ableitung auch null. Wenn die Energie nicht erhalten ist, ergibt die Ableitung genau die Energie, die pro Eigenzeit für diesen Beobachter im Volumen entsteht oder vernichtet, d.h. nicht durch Ströme durch den Rand verursacht wird. zur Bilanz beitragen. Der Vektor n ist hier normal zur "Mantelfläche" des Vierervolumens, über dessen gesamten Rand integriert wird. Wenn die Energie erhalten ist, verschwindet das komplette Randintegral unabhängig von t. Also ist die Ableitung auch null. Wenn die Energie nicht erhalten ist, ergibt die Ableitung genau die Energie, die pro Eigenzeit für diesen Beobachter im Volumen entsteht oder vernichtet, d.h. nicht durch Ströme durch den Rand verursacht wird.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 23. März 2022 11:20 Titel: TomS Verfasst am: 23. März 2022 11:20 Titel: |
 |
|
Danke, so macht das bzgl. der Indizes Sinn.
Trotzdem bleibt für mich die Frage, wie du von dem Beobachter sprechen kannst, während du tatsächlich ein Beobachterfeld innerhalb des Volumens hast.
Natürlich ist es naheliegend, mitbewegte Beobachter anzusetzen, aber doch nicht zwingend. Betrachten wir z.B. eine Skala, auf der sowohl die Expansion als auch Inhomogenitäten relevant sind, z.B. eine Kugel, die die Sloan Great Wall mit einer Ausdehnung von 1.3 Mrd LJ. enthält.
Dann wäre zunächst eine beliebige Schar von Beobachtern zu betrachten, d.h.
}} \, T^{ab} \, u_a \, u_b)
Dieses Beobachterfeld u muss nicht mitbewegt sein, d.h. es entspricht i.A. nicht der Vierergeschwindigkeit v im Energie-Impuls-Tensor
)
Würden wir dieses E jetzt als „verallgemeinerte Energie“ bezeichnen? Was können wir bzgl. der Erhaltung sagen? Für allgemeines u wahrscheinlich nichts.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 23. März 2022 14:05 Titel: index_razor Verfasst am: 23. März 2022 14:05 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
Trotzdem bleibt für mich die Frage, wie du von dem Beobachter sprechen kannst, während du tatsächlich ein Beobachterfeld innerhalb des Volumens hast.
|
Das Feld ergibt sich doch automatisch, wenn ich eine 3dimensionale raumartige Hyperfläche als Integrationsgebiet definiere, nämlich aus der Menge aller zukunftsgerichteten Normalen an diese Fläche. Natürlich hängen alle Schlußfolgerungen im allgemeinen von der Fläche ab und damit auch vom Beobachter. Aber ob ich einen Beobachter plus Gleichzeitgkeits-Hyperfläche oder eine Schar von Beobachtern einführe, macht denke ich, keinen großen Unterschied. (Abgesehen von technischen Fragen, die wahrscheinlich nicht viel mit der Diskussion zu tun haben.) Mindestens zwei solcher Hyperflächen benötige ich nun. Ihre Ränder müssen irgendwie im Vierdimensionalen verbunden sein, damit ich eine geschlossene Oberfläche habe. Die Art dieser Verbindung bestimmt nur wieviel Energie zu welcher Zeit aus- oder einströmt. Wenn diese Oberfläche einmal definiert ist, kann ich eine Energiebilanz für sie aufstellen. (Die Quellendichte im Inneren hängt natürlich auch von der Bewegung der Beobachter im Inneren ab. Ihr Integral aber, wegen des Satzes von Gauß, nicht.)
| Zitat: |
Natürlich ist es naheliegend, mitbewegte Beobachter anzusetzen, aber doch nicht zwingend. Betrachten wir z.B. eine Skala, auf der sowohl die Expansion als auch Inhomogenitäten relevant sind, z.B. eine Kugel, die die Sloan Great Wall mit einer Ausdehnung von 1.3 Mrd LJ. enthält.
Dann wäre zunächst eine beliebige Schar von Beobachtern zu betrachten, d.h.
}} \, T^{ab} \, u_a \, u_b)
Dieses Beobachterfeld u muss nicht mitbewegt sein, d.h. es entspricht i.A. nicht der Vierergeschwindigkeit v im Energie-Impuls-Tensor
)
|
Klar, ich will auch nicht erzwingen mitbewegte Beobachter zu wählen. Ich wollte aber festhalten, daß Aussagen über mitbewegte Beobachter physikalisch sinnvoll und nicht willkürlich sind.
Ich habe ja außerdem schon Vermutungen darüber geäußert wie ich mir die Situation von nicht-mitbewegten Beobachtern vorstelle. Solche Beobachter definieren also den Energiestrom
\gamma v^a + Pu^a )
mit Dichte
\gamma^2 - P)
Jetzt müßten wir die Gleichzeitigkeitshyperflächen zu zwei verschiedenen Zeiten inklusive Metrik definieren. Außerdem hängt die genaue Form von 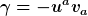 von der Relativbewegung zur Materie ab und könnte theoretisch orts- und zeitabhängig sein. Die Mantelflächen sollen nun vermutlich von der Relativbewegung zur Materie ab und könnte theoretisch orts- und zeitabhängig sein. Die Mantelflächen sollen nun vermutlich 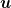 enthalten und nicht wie vorher enthalten und nicht wie vorher  . Dann wird . Dann wird
\gamma n_a u^a)
überall aus dem Gebiet strömen, was wir berücksichtigen müssen. (Anders als vorher ist n nun nicht mehr orthogonal zur Vierergeschwindigkeit der Materie.) In das Skalarpodukt geht wieder  ein. Wenn ein. Wenn  konstant ist, wird es, denke ich, auf dieselbe Schlußfolgerung hinauslaufen wie vorher, daß die Energie abnimmt. Aber wenn nicht, wäre das m.E. auch nicht schlimm. Es beweist nicht, daß die ursprüngliche Aussage physikalisch bedeutungslos ist, sondern nur, daß für verschiedene Beobachter verschiedene physikalisch sinnvolle Aussagen gelten, was ja ohnehin oft der Fall ist. konstant ist, wird es, denke ich, auf dieselbe Schlußfolgerung hinauslaufen wie vorher, daß die Energie abnimmt. Aber wenn nicht, wäre das m.E. auch nicht schlimm. Es beweist nicht, daß die ursprüngliche Aussage physikalisch bedeutungslos ist, sondern nur, daß für verschiedene Beobachter verschiedene physikalisch sinnvolle Aussagen gelten, was ja ohnehin oft der Fall ist.
| Zitat: |
Würden wir dieses E jetzt als „verallgemeinerte Energie“ bezeichnen?
|
Ich würde es einfach als die von den Beobachtern u gemessene Energie im Volumen V bezeichnen. Bei Energien müssen wir immer sagen auf welche Beobachter sie sich beziehen.
| Zitat: |
Was können wir bzgl. der Erhaltung sagen? Für allgemeines u wahrscheinlich nichts. |
Genau. Aber für allgemeines u können wir nie etwas definitives sagen. Selbst in einem statischen Universum können wir beliebig beschleunigte Beobachter einführen, und die von ihnen gemessene Energie macht im wesentlichen was sie will.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 23. März 2022 14:49 Titel: TomS Verfasst am: 23. März 2022 14:49 Titel: |
 |
|
Jetzt sind wir uns einig.
Ich glaube, du hattest oben geschrieben, man müsse zwei Fragen auseinanderhalten: die Frage nach der Definition der Energie, und die Frage nach ihrer Erhaltung.
Das haben wir jetzt aufgedröselt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Ich
Anmeldungsdatum: 11.05.2006
Beiträge: 913
Wohnort: Mintraching
|
 Ich Verfasst am: 24. März 2022 16:40 Titel: Ich Verfasst am: 24. März 2022 16:40 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Ich hat Folgendes geschrieben: |
Im Ruhesystem von Punkt 1 hingegen (in nicht expandierenden Koordinaten) sieht die Sache anders aus: Zur Zeit 0 entsteht bei Punkt 1 ein Photon mit Energie f, an Punkt zwei ein um 2dx*f/c rotverschobenes Photon. Nach dt erreichen diese die Grenze, aus Volumen 1 geht ein Photon mit f raus und eins mit f-2dxf/c kommt rein. Deswegen nimmt die Energie in diesem Volumen ab. Nicht, weil sie "verschwindet", sondern weil sie ins Nachbarvolumen rüberströmt.
|
Ich habe keine Ahnung, wie du zu dieser Beschreibung kommst. Du behauptest, die Energie zur späteren Zeit sei für Beobachter 1 um genau den Betrag des Energiestroms aus dem Volumen geringer als zur früheren Zeit. Diese Aussage -- ob richtig oder falsch -- hat jedenfalls nicht das geringste mit irgendwelchen Koordinaten zu tun, sondern damit ob das Integral über die Viererdivergenz der Energistromdichte für diesen Beobachter über den definierten Raumzeitbereich verschwindet, d.h.
\sqrt{g}\dd^4 x = 0.)
Das ist eine koordinatenunabhängige Größe. Die Energiestromdichte 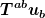 hängt zwar vom Beobachter ab, aber das ist nicht der Punkt. Die Frage ist, ob es einen Beobachter gibt, für den diese Divergenz verschwindet. Das hast du für das Robertson-Walker-Universum nicht gezeigt und ich denke auch nicht, daß es stimmen kann. hängt zwar vom Beobachter ab, aber das ist nicht der Punkt. Die Frage ist, ob es einen Beobachter gibt, für den diese Divergenz verschwindet. Das hast du für das Robertson-Walker-Universum nicht gezeigt und ich denke auch nicht, daß es stimmen kann.
|
Wir reden komplett aneinander vorbei. Nicht verwunderlich, weil ich mich anfangs ja falsch ausgedrückt hatte. Hier nochmal, was ich sagen will:
1. Im strahlungsdominierten Universum geht die Energiedichte für mitbewegte Beobachter wie 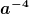 . Das ist Fakt und hat nichts mit speziellen Koordinaten zu tun. . Das ist Fakt und hat nichts mit speziellen Koordinaten zu tun.
2. Das bedeutet noch nicht, dass Energie "verschwindet". Ein Faktor 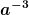 kommt alleine von der Vergrößerung des mitbewegten Volumens. kommt alleine von der Vergrößerung des mitbewegten Volumens.
3. Ein weiterer Faktor 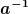 kommt von der kosmologischen Rotverschiebung der Strahlung. Ich beschäftige mich nur mit diesem Faktor, damit wir nicht in weitere Details abgleiten. kommt von der kosmologischen Rotverschiebung der Strahlung. Ich beschäftige mich nur mit diesem Faktor, damit wir nicht in weitere Details abgleiten.
So weit ist noch nichts strittig, denke ich. Deine Aussage war:
| index_razor hat Folgendes geschrieben: | | Aus den Friedmann-Gleichungen folgt aber für die Energiedichte im expandierenden Universum. Also gilt für die Energie ein lokaler "Nichterhaltungssatz" mit negativer Quellendichte. Deshalb ist es schon sinnvoll zu sagen, daß Energie verschwindet. |
4. Ich deute deine Aussage so: Weil aus Symmetriegründen keine Energie aus der Oberfläche des betrachteten 3-Volumens austritt, kann man eindeutig sagen, dass hier lokal Energie verschwindet.
5. Ich behaupte, dass diese Aussage koordinatenabhängig ist, und dass bei Verwendung von Normalkoordinaten die Energie einfach aus dem 3-Volumen fließt. Die Photonenenergie nimmt immer noch mit 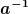 ab, aber das ist ganz einfach damit erklärt, dass energiereichere Photonen austreten und durch energieärmere aus anderen Regionen ersetzt werden. Und ich behaupte, dass deswegen die eindeutige Aussage, dass lokal Energie verschwinde, "zu stark" ist. ab, aber das ist ganz einfach damit erklärt, dass energiereichere Photonen austreten und durch energieärmere aus anderen Regionen ersetzt werden. Und ich behaupte, dass deswegen die eindeutige Aussage, dass lokal Energie verschwinde, "zu stark" ist.
Habe ich das richtig wiedergegeben? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 24. März 2022 16:59 Titel: TomS Verfasst am: 24. März 2022 16:59 Titel: |
 |
|
| Ich hat Folgendes geschrieben: | 4. … kann man eindeutig sagen, dass hier lokal Energie verschwindet.
5. Ich behaupte, dass diese Aussage koordinatenabhängig ist … |
index_razor’s zuletzt diskutierte Gleichungen sind aber koordinatenunabhängigen ;-)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 24. März 2022 17:02 Titel: TomS Verfasst am: 24. März 2022 17:02 Titel: |
 |
|
| Ich hat Folgendes geschrieben: | 4. … kann man eindeutig sagen, dass hier lokal Energie verschwindet.
5. Ich behaupte, dass diese Aussage koordinatenabhängig ist … |
index_razor’s Gleichungen sind aber koordinatenunabhängig, die Energie E[u] ist ein Skalar ;-)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Ich
Anmeldungsdatum: 11.05.2006
Beiträge: 913
Wohnort: Mintraching
|
 Ich Verfasst am: 24. März 2022 21:53 Titel: Ich Verfasst am: 24. März 2022 21:53 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Ich hat Folgendes geschrieben: | 4. … kann man eindeutig sagen, dass hier lokal Energie verschwindet.
5. Ich behaupte, dass diese Aussage koordinatenabhängig ist … |
index_razor’s Gleichungen sind aber koordinatenunabhängig, die Energie E[u] ist ein Skalar ;-) |
Die Energie E[u] ist ja auch immer die selbe, siehe Punkt 1. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 25. März 2022 07:55 Titel: index_razor Verfasst am: 25. März 2022 07:55 Titel: |
 |
|
| Ich hat Folgendes geschrieben: | Deine Aussage war:
| index_razor hat Folgendes geschrieben: | | Aus den Friedmann-Gleichungen folgt aber für die Energiedichte im expandierenden Universum. Also gilt für die Energie ein lokaler "Nichterhaltungssatz" mit negativer Quellendichte. Deshalb ist es schon sinnvoll zu sagen, daß Energie verschwindet. |
4. Ich deute deine Aussage so: Weil aus Symmetriegründen keine Energie aus der Oberfläche des betrachteten 3-Volumens austritt, kann man eindeutig sagen, dass hier lokal Energie verschwindet.
|
Nein, das ist nicht der Grund. Die gesamte Energiebilanz ist
 - E(t_0) + \int_{t_0}^{t_1}\int_{\partial V(t)} \text{Nettostromdichte aus V(t)} = \text{netto erzeugte Energie}.\quad\text{(1)})
Das ist immer negativ, egal wie groß der Nettostrom aus dem Volumen ist. Aber wenn er null ist, wie beim mitbewegten Volumen, ist die verlorene Energie natürlich einfach die Differenz der beiden Energien zwischen End- und Anfangszeit, also im homogenen Universum trivial auszurechnen.
Man kann also nicht eindeutig sagen, wieviel Energie zwischen zwei Zeiten verlorengegangen ist, weil das nicht nur vom Anfangs- und Endvolumen, sondern auch von dessen Änderung in der Zwischenzeit abhängt. Wenn man einen Strom zur Erhaltungsgröße integriert, richtet man es ja normalerweise so ein, daß alle Ströme aus den Randflächen verschwinden, typischerweise dadurch, daß man sie ins Unendliche verlegt. Das bringt hier natürlich nichts. Aber mitbewegte Volumina bieten sich zu dem Zweck natürlich auch an.
Aber egal welches Volumen man wählt, es ist unmöglich, daß exakt soviel Energie ausströmt, wie am Ende weniger vorhanden ist. Also ist deine zentrale Behauptung falsch. Es geht immer Energie verloren.
Warum? Die Energiebilanz für mitbewegte Beobachter ist nichts anderes als das Gaußsche Gesetz für das Vektorfeld 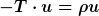 . Die rechte Seite von (1) ist das Integral über die Quellendichte . Die rechte Seite von (1) ist das Integral über die Quellendichte
} \nabla\cdot(T\cdot u)\sqrt{g}\dd t\ \dd^3 x)
und der Integrand ist
 = -3P\frac{\dot a}{a})
Das ist ein Skalar und für Strahlung überall und zu allen Zeiten negativ. (Die Energie von Staub bleibt aber tatsächlich erhalten.) Das gilt übrigens nicht nur für mitbewegte Beobachter, sondern auch solche die sich mit konstanter Geschwindigkeit relativ zum Hintergrund bewegen. Die stellen eine andere Quellendichte fest, aber sie ist immer noch negativ.
| Zitat: |
5. Ich behaupte, dass diese Aussage koordinatenabhängig ist, und dass bei Verwendung von Normalkoordinaten die Energie einfach aus dem 3-Volumen fließt. Die Photonenenergie nimmt immer noch mit 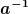 ab, aber das ist ganz einfach damit erklärt, dass energiereichere Photonen austreten und durch energieärmere aus anderen Regionen ersetzt werden. ab, aber das ist ganz einfach damit erklärt, dass energiereichere Photonen austreten und durch energieärmere aus anderen Regionen ersetzt werden.
|
Nein, das kann man eben nicht so erklären. Deine Behauptung ist äquivalent zu
 - E(t_0) = -\int_{t_0}^{t_1}\int_{\partial V(t)} \text{Nettostromdichte aus V(t)}.)
Wenn es so wäre, müßte
 = -3P\frac{\dot a}{a}=-\rho\frac{\dot a}{a})
im raumzeitlichen Mittel verschwinden. Es ist aber immer negativ, also ist auch das Integral negativ und selbst nach Abzug des Nettostroms bleibt immer noch eine Differenz übrig. Folglich ist auch die Energiebilanz immer negativ, egal welchen Bereich der Raumzeit du betrachtest. (Es ist erst recht egal, welche Koordinaten du über diesen Bereich legst. In Normalkoordinaten ändert sich daran rein gar nichts.)
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
 |
Ich
Anmeldungsdatum: 11.05.2006
Beiträge: 913
Wohnort: Mintraching
|
 Ich Verfasst am: 25. März 2022 16:53 Titel: Ich Verfasst am: 25. März 2022 16:53 Titel: |
 |
|
Ich habe mit mäßigem Erfolg versucht, deine Rechnungen und Definitionen aus den letzten Beiträgen nachzuvollziehen. Das ist mir noch nicht gelungen, ich bin leider nicht mehr sehr firm darin. Ich habe auch nicht gefunden, wo du falsch abbiegst.
Mir ist aber beim Nachlese eine Aussage von dir ()am 23.3.) aufgefallen, die vielleicht ein Hinweis ist:
| Zitat: | | Ganz und gar nicht. Wie gesagt, dann müßtest du auch die Aussage "Das Universum ist homogen und isotrop" für "zu stark" halten. Die basiert nämlich auf exakt denselben Voraussetzungen. Das tust du aber nicht, nehme ich mal an. |
Dass das Universum homogen ist, ist tatsächlich koordinatenabhängig. Insbesondere ist das Universum ausschließlich in den Koordinaten homogen, in denen der Energiefluß über die Grenze eines mitbewegten Volumens verschwindet. Diese Homogenitätsforderung hast du vielleicht auf alle lokalen Koordinatensysteme verallgemeinert.
Ich mache mal die Gegenrechnung:
Wir betrachten ein kleines, konstantes sphärisches Volumen mit Radius r. Konstant heißt: nicht mitbewegt, die Vierergeschwindigkeit der Grenze ist parallel zu der des Beobachters im Zentrum.
Das Fluid hat an der Grenze eine Relativgescwindigkeit von
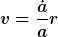 . .
Die 0r-Komponente des Energie-Impulstensors kriegt man also durch einen Boost mit v:
 = \gamma^2\frac{\dot a}{a}r(\rho+p)\simeq \frac{\dot a}{a}r(\rho+p))
Der Energiestrom aus dem Volumen ist
)
Die Abnahme der Energiedichte ist also:
)
Hier ist der zusätzliche Term durch den Druck p schon mit eingespeist, weil das Fluid für einen Beobachter am Rand eben nicht mehr homogen und isotrop ist. Die Abnahme der Energiedichte ist also vollständig durch den Fluss über die Grenze erklärt. Anschaulich fließt wie gesagt wegen des Dopplereffekts wärmere Strahlung raus als rein.
Der Effekt ist linear in r und t, das hat also nichts mit Raumzeitkrümmung zu tun. Das funktioniert in flacher Raumzeit genauso, z.B. bei vernachlässigbarer Energiedichte (Milne). Das ist dann analog zu Rindler-Koordinaten: Durch eine Koordinatentrafo hast du da ein Gravitationsfeld in flacher Raumzeit, und hier hast du verschwindende Energie in flacher Raumzeit, trotz zeitartigem Killingfeld und allem. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 25. März 2022 19:35 Titel: index_razor Verfasst am: 25. März 2022 19:35 Titel: |
 |
|
| Ich hat Folgendes geschrieben: | Ich habe mit mäßigem Erfolg versucht, deine Rechnungen und Definitionen aus den letzten Beiträgen nachzuvollziehen. Das ist mir noch nicht gelungen, ich bin leider nicht mehr sehr firm darin. Ich habe auch nicht gefunden, wo du falsch abbiegst.
Mir ist aber beim Nachlese eine Aussage von dir ()am 23.3.) aufgefallen, die vielleicht ein Hinweis ist:
| Zitat: | | Ganz und gar nicht. Wie gesagt, dann müßtest du auch die Aussage "Das Universum ist homogen und isotrop" für "zu stark" halten. Die basiert nämlich auf exakt denselben Voraussetzungen. Das tust du aber nicht, nehme ich mal an. |
Dass das Universum homogen ist, ist tatsächlich koordinatenabhängig. Insbesondere ist das Universum ausschließlich in den Koordinaten homogen, in denen der Energiefluß über die Grenze eines mitbewegten Volumens verschwindet. Diese Homogenitätsforderung hast du vielleicht auf alle lokalen Koordinatensysteme verallgemeinert.
|
Solange du meine Behauptungen nicht verstehst, ist es etwas voreilig in ihnen nach Fehlern zu suchen. Ich verwende keine speziellen Koordinaten, sondern nur die kovariante Viererdivergenz der Energiestromdichte. (Das ist eine Invariante, also ist auch egal in welchen Koordinaten ich sie berechne.) Dir ist anscheinend nicht klar, was diese Größe mit der Energiebilanz zu tun hat. Vielleicht sollten wir das als erstes klären, denn ich glaube das ist bei weitem der einfachste Zugang zu dem Thema. Ich vermute, dadurch wird auch deutlicher werden, wo der Fehler in deiner eigenen Bilanzgleichung liegt.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
 |
Ich
Anmeldungsdatum: 11.05.2006
Beiträge: 913
Wohnort: Mintraching
|
 Ich Verfasst am: 25. März 2022 20:35 Titel: Ich Verfasst am: 25. März 2022 20:35 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Solange du meine Behauptungen nicht verstehst, ist es etwas voreilig in ihnen nach Fehlern zu suchen. |
Da ist grundsätzlich was Wahres dran. Es ist nur so, dass ich wegen Beispielen, die nichts mit deiner Argumentation zu tun haben. überzeugt bin, dass deine Schlussfolgerung falsch ist. Also suche ich nach dem Fehler. Wobei dieses Suchen ja die Möglichkeit einschließt, dass ich Unrecht habe und ich deine Herleitung als richtig erkenne.
Meine Gegenbeispiele sind:
1. Wie schon gesagt das FLRW-Universum mit verschwindender Energiedichte. Das ist eine flache Raumzeit, in der definitiv Energieerhaltung gilt. Es gibt sogar eine schöne Koordinatentrafo von RW nach Minkowski. Trotzdem zeigt deine Ableitung dafür verschwindende Energie an.
2. Das Birkhoff-Theorem. Jede FLRW-Metrik ist kugelsymmetrisch um jeden Punkt. Also ist die Raumzeitgeometrie eines kleinen, sphärischen Ausschnitts in einem ansonsten leeren Universum exakt dieselbe wie im gänzlich gefüllten Universum. Ein kleiner Gas- oder Strahlungsball im leeren Universum unterliegt aber definitiv in beliebig guter Näherung der Energieerhaltung, da kann nicht einfach substanziell Energie verschwinden, wie es nach deiner Schlussfolgerung aber geschehen soll.
3. Meine Rechnung. Sie beweist explizit das, was ich sage. Sie muss also falsch sein, wenn deine Ableiitung stimmt. Das ist natürlich nicht ausgeschlossen, ich bin ja ganz schön eingerostet in diesen Themen. So wahnsinnig kompliziert ist sie aber auch nicht, du kannst mir den etwaigen Fehler bestimmt schnell zeigen.
4. Die Heuristik hinter meiner Rechnung. Also das Beispiel mit den rotverschobenen Photonen vor 3 Beiträgen. Das zeigt unmittelbar und ohne Rechnung, dass über die Grenze mehr fließt als 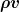 . .
| Zitat: | | Ich verwende keine speziellen Koordinaten, sondern nur die kovariante Viererdivergenz der Energiestromdichte. (Das ist eine Invariante, also ist auch egal in welchen Koordinaten ich sie berechne.) Dir ist anscheinend nicht klar, was diese Größe mit der Energiebilanz zu tun hat. Vielleicht sollten wir das als erstes klären, denn ich glaube das ist bei weitem der einfachste Zugang zu dem Thema. |
Das ist wohl nicht der einfachste Zugang, aber gerne. Vielleicht kannst du mir als erstes die Quellendichte im Volumenintegral erklären, da stehe ich auf dem Schlauch.
| Zitat: | | Ich vermute, dadurch wird auch deutlicher werden, wo der Fehler in deiner eigenen Bilanzgleichung liegt. |
Bitte nicht vermuten, sondern zeigen. Auch wenn ich überzeugt bn, Recht zu haben, bin ich umso mehr daran interessiert, eines besseren belehrt zu werden. Dann kann man am meisten lernen. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 26. März 2022 08:58 Titel: index_razor Verfasst am: 26. März 2022 08:58 Titel: |
 |
|
| Ich hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Solange du meine Behauptungen nicht verstehst, ist es etwas voreilig in ihnen nach Fehlern zu suchen. |
Da ist grundsätzlich was Wahres dran. Es ist nur so, dass ich wegen Beispielen, die nichts mit deiner Argumentation zu tun haben. überzeugt bin, dass deine Schlussfolgerung falsch ist. Also suche ich nach dem Fehler. Wobei dieses Suchen ja die Möglichkeit einschließt, dass ich Unrecht habe und ich deine Herleitung als richtig erkenne.
|
Wenn du nicht ansatzweise verstehst, was ich eigentlich behaupte, argumentierst du natürlich am Thema vorbei. Das ist zumindest auch ein Problem deiner Gegenbeispiele.
| Zitat: |
Meine Gegenbeispiele sind:
1. Wie schon gesagt das FLRW-Universum mit verschwindender Energiedichte. Das ist eine flache Raumzeit, in der definitiv Energieerhaltung gilt. Es gibt sogar eine schöne Koordinatentrafo von RW nach Minkowski. Trotzdem zeigt deine Ableitung dafür verschwindende Energie an.
|
Da eine flache Raumzeit statisch ist, gilt darin nach meiner Aussage Energieerhaltung. Darauf habe ich schon hingewiesen. Das solltest du also wissen. (Vielleicht führt dich hier die "Koordinatentrafo von RW nach Minkowksi" in die Irre. Das ist aber wieder ein anderes Problem, das nicht direkt etwas mit dem Thema zu tun hat.)
| Zitat: |
2. Das Birkhoff-Theorem. Jede FLRW-Metrik ist kugelsymmetrisch um jeden Punkt. Also ist die Raumzeitgeometrie eines kleinen, sphärischen Ausschnitts in einem ansonsten leeren Universum exakt dieselbe wie im gänzlich gefüllten Universum. Ein kleiner Gas- oder Strahlungsball im leeren Universum unterliegt aber definitiv in beliebig guter Näherung der Energieerhaltung, da kann nicht einfach substanziell Energie verschwinden, wie es nach deiner Schlussfolgerung aber geschehen soll.
|
Die Aussage des Birkhoff-Theorems bezieht sich auf materiefreie Bereiche einer kugelsymmetrischen Raumzeit. Wenn es keine solchen Bereiche gibt, spielt es keine Rolle, daß die Raumzeit um jeden Punkt kugelsymmetrisch ist.
Die Behauptung des Theorems ist, daß diese Bereiche statisch und asymptotisch flach sind. Beides trifft auf das Robertson-Walker-Universum natürlich nicht zu. Und wie ich bereits sagte, folgt aus meiner Rechnung Energieerhaltung für statische Raumzeiten.
Sie gilt also natürlich exakt für den kleinen Gas- oder "Strahlungs"ball im ansonsten leeren Universum. Folglich ist das einzige Problem hier wieder, daß du den Inhalt meiner Schlußfolgerung gar nicht verstanden hast.
| Zitat: |
3. Meine Rechnung. Sie beweist explizit das, was ich sage. Sie muss also falsch sein, wenn deine Ableiitung stimmt. Das ist natürlich nicht ausgeschlossen, ich bin ja ganz schön eingerostet in diesen Themen. So wahnsinnig kompliziert ist sie aber auch nicht, du kannst mir den etwaigen Fehler bestimmt schnell zeigen.
|
Es ist ja kein simpler Rechenfehler. Das Problem besteht schon darin, daß du anscheinend nicht weißt, wie man einen lokalen Erhaltungssatz in der ART formuliert. Das ist ein sicher schwieriger auszuräumendes konzeptionelles Problem. Und es hat vermutlich nicht mal speziell etwas mit Energieerhaltung zu tun.
| Zitat: |
4. Die Heuristik hinter meiner Rechnung. Also das Beispiel mit den rotverschobenen Photonen vor 3 Beiträgen. Das zeigt unmittelbar und ohne Rechnung, dass über die Grenze mehr fließt als 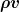 . .
|
Eine Heuristik habe ich auch: im homogenen isotropen Universum ist der Energiestrom überall null und die Dichte überall konstant. Also bedeutet lokale Energieerhaltung 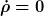 bzw. in einem expandierenden Universum mit denselben Eigenschaften bzw. in einem expandierenden Universum mit denselben Eigenschaften 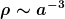 . Wie du sicher gern bestätigen wirst, haben solche Argumente für andere oft wenig Überzeugungskraft. . Wie du sicher gern bestätigen wirst, haben solche Argumente für andere oft wenig Überzeugungskraft.
| Zitat: |
| Zitat: | | Ich verwende keine speziellen Koordinaten, sondern nur die kovariante Viererdivergenz der Energiestromdichte. (Das ist eine Invariante, also ist auch egal in welchen Koordinaten ich sie berechne.) Dir ist anscheinend nicht klar, was diese Größe mit der Energiebilanz zu tun hat. Vielleicht sollten wir das als erstes klären, denn ich glaube das ist bei weitem der einfachste Zugang zu dem Thema. |
Das ist wohl nicht der einfachste Zugang, aber gerne. Vielleicht kannst du mir als erstes die Quellendichte im Volumenintegral erklären, da stehe ich auf dem Schlauch.
|
Das habe ich gerade in mehreren Beiträgen versucht. Deine einzige Reaktion war "Sorry, ich bin eingerostet und kann deswegen deinen Fehler nicht finden." Deshalb will ich im Augenblick eigentlich nicht noch mehr Zeit investieren. Wenn es dir ernst ist, kannst du m.E. viel hilfreiches in Wald, Kap. 4 (inklusive Verweise auf den Anhang) finden. Oder du stellst eine konkrete Frage zu meinem Argument.
| Zitat: |
| Zitat: | | Ich vermute, dadurch wird auch deutlicher werden, wo der Fehler in deiner eigenen Bilanzgleichung liegt. |
Bitte nicht vermuten, sondern zeigen. Auch wenn ich überzeugt bn, Recht zu haben, bin ich umso mehr daran interessiert, eines besseren belehrt zu werden. Dann kann man am meisten lernen. |
Es ist ja nicht so, daß ich hier noch nichts gezeigt hätte, was dich hätte belehren können. Aber solange deine Einstellung ist, daß du das alles nicht verstehen mußt, weil es ja ohnehin falsch ist, werden wir nicht mehr sehr weit kommen.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
 |
|
|















