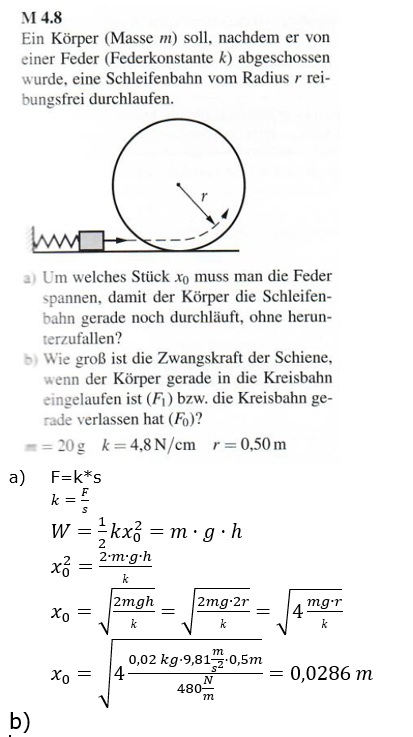
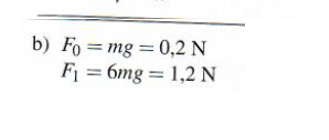Startseite
 
 
Fragen
 
Suchen
 
Formeleditor
 
Über Uns
 
 
  RegistrierenRegistrieren   LoginLogin   FAQFAQ    SuchenSuchen   
Energieerhaltung Looping
 
Neue Frage »
Antworten »
    Foren-Übersicht -> Mechanik
Autor Nachricht
MMchen60



Anmeldungsdatum: 31.01.2021
Beiträge: 207
Wohnort: Heilbronn
Beitrag MMchen60 Verfasst am: 20. Jan 2023 19:22    Titel: Energieerhaltung Looping Antworten mit Zitat
Hallo, liebe Forumsgemeinde,
ich habe Verständnisschwierigkeiten mit der Aufgabe im Anhang.
Aufgabenteil a) Es soll offensichtlich die Spannenergie der Feder in potentielle Energie so umgewandelt werden, dass das abgeschossene Teil im höchsten Punkt nicht herunterfällt. Gut, ich habe das rechnerisch nachvollzogen und komme da bevor ich Werte einsetze zu einer 4 unter der Wurzel.
Die Aufgabe stammt aus dem Übungsbuch Physik im Carl-Hanser-Verlag. Dort sind am Ende nur Ergebnisse angegeben, keine Lösungswege. Das Buch kommt dabei auf die Formel .
Wie kommen die auf die 5?
Dann zu b), was versteht der Autor der Aufgabe unter und ?
Vielen Dank für Antwort

physikerboard01.png
 Beschreibung:
 Dateigröße:  168.49 KB
 Angeschaut:  1093 mal

physikerboard01.png
Myon



Anmeldungsdatum: 04.12.2013
Beiträge: 5852
Beitrag Myon Verfasst am: 20. Jan 2023 20:15    Titel: Antworten mit Zitat
Zu a): In Deiner Gleichung



hast Du vergessen, dass die Masse m am obersten Punkt auch eine kinetische Energie haben muss - so gross, dass die Gewichtskraft gerade der nötigen Zentripetalkraft für die Kreisbewegung entspricht (v^2/r=g).

Zu b): F1 und F0 sollen einfach die beiden Zwangskräfte sein (Normalkraft der Schiene auf die Masse) an den beschriebenen Punkten. Wobei F1 offenbar die Kraft ist gerade kurz nach dem Einlaufen in die Kreisbahn. Am Punkt, wo die Kreisbahn beginnt, hat die Kraft eine Unstetigkeitsstelle, d.h. sie springt von 0 auf die Kraft F1.
MMchen60



Anmeldungsdatum: 31.01.2021
Beiträge: 207
Wohnort: Heilbronn
Beitrag MMchen60 Verfasst am: 21. Jan 2023 09:25    Titel: Antworten mit Zitat
Myon hat Folgendes geschrieben:

Zu b): F1 und F0 sollen einfach die beiden Zwangskräfte sein (Normalkraft der Schiene auf die Masse) an den beschriebenen Punkten. Wobei F1 offenbar die Kraft ist gerade kurz nach dem Einlaufen in die Kreisbahn. Am Punkt, wo die Kreisbahn beginnt, hat die Kraft eine Unstetigkeitsstelle, d.h. sie springt von 0 auf die Kraft F1.


Hallo Myon vielen Dank, ja jetzt ist es mir klar. Doch noch eine Frage zu b). F0 mit m * g dann klar. Aber wie kommt man da auf F1 gemäß Lösung, siehe Anhang?

physikerboard02.png
 Beschreibung:
 Dateigröße:  24.43 KB
 Angeschaut:  1018 mal

physikerboard02.png
Myon



Anmeldungsdatum: 04.12.2013
Beiträge: 5852
Beitrag Myon Verfasst am: 21. Jan 2023 10:03    Titel: Antworten mit Zitat
MMchen60 hat Folgendes geschrieben:
Aber wie kommt man da auf F1 gemäß Lösung, siehe Anhang?

Indem Du für einen Punkt gleich nach dem Einlaufen in die Kreisbahn die Bewegungsgleichung



aufstellst und nach F1 löst. Die Beschleunigung und die Kräfte wirken alle in vertikaler Richtung, und vu ist die Geschwindigkeit "unten". Übrigens habe ich oben falsch geschrieben, die Normalkraft ändert beim Einlaufen nicht von 0 auf F1, sondern von m*g auf F1.
MMchen60



Anmeldungsdatum: 31.01.2021
Beiträge: 207
Wohnort: Heilbronn
Beitrag MMchen60 Verfasst am: 24. Jan 2023 19:40    Titel: Antworten mit Zitat
Myon hat Folgendes geschrieben:

Indem Du für einen Punkt gleich nach dem Einlaufen in die Kreisbahn die Bewegungsgleichung



aufstellst und nach F1 löst. Die Beschleunigung und die Kräfte wirken alle in vertikaler Richtung, und vu ist die Geschwindigkeit "unten". Übrigens habe ich oben falsch geschrieben, die Normalkraft ändert beim Einlaufen nicht von 0 auf F1, sondern von m*g auf F1.


Hallo, danke, habe ich mal gemacht, komme aber auf nur 5 mg, siehe Anhang, in der Lösung steht aber 6mg. Habe ich was vergessen?

physikerboard03.png
 Beschreibung:

Download
 Dateiname:  physikerboard03.png
 Dateigröße:  13.17 KB
 Heruntergeladen:  45 mal
Myon



Anmeldungsdatum: 04.12.2013
Beiträge: 5852
Beitrag Myon Verfasst am: 24. Jan 2023 20:37    Titel: Antworten mit Zitat
Mit den Bezeichnungen vu und vo für die Geschwindigkeiten oben und unten würde die 2. Gleichung lauten:



Für die Mindestgeschwindigkeit am höchsten Punkt gilt, vgl. weiter oben, vo^2/r=g. Aus der Energieerhaltung:



und damit

MMchen60



Anmeldungsdatum: 31.01.2021
Beiträge: 207
Wohnort: Heilbronn
Beitrag MMchen60 Verfasst am: 25. Jan 2023 09:56    Titel: Antworten mit Zitat
Myon hat Folgendes geschrieben:
Mit den Bezeichnungen

Möchte mich kurz nochmal melden und meinen Dank aussprechen.
VG M. Müller
Myon



Anmeldungsdatum: 04.12.2013
Beiträge: 5852
Beitrag Myon Verfasst am: 25. Jan 2023 14:23    Titel: Antworten mit Zitat
Bitte gern geschehen. Und danke für den Dank, das ist nicht unbedingt üblich..;-)
Neue Frage »
Antworten »
    Foren-Übersicht -> Mechanik

Verwandte Themen - die Neuesten
 Themen   Antworten   Autor   Aufrufe   Letzter Beitrag 
Keine neuen Beiträge Looping Mindestgeschwindigkeit 1 Gast 567 01. Jan 2024 19:13
Myon Letzten Beitrag anzeigen
Keine neuen Beiträge Energieerhaltung 3 Gast 568 02. Nov 2023 18:16
TomS Letzten Beitrag anzeigen
Keine neuen Beiträge Newtonsche Gesetze, Energieerhaltung 5 masterchief 1470 10. Jun 2023 17:38
roycy Letzten Beitrag anzeigen
Dieses Thema ist gesperrt, du kannst keine Beiträge editieren oder beantworten. FAQ - Energieerhaltung im Fall destruktiver Interferenz 1 TomS 21003 05. Apr 2023 22:50
ML Letzten Beitrag anzeigen
Dieses Thema ist gesperrt, du kannst keine Beiträge editieren oder beantworten. Energieerhaltung Geschwindigkeit berechnen 2 Dreister 831 10. Dez 2022 22:01
Steffen Bühler Letzten Beitrag anzeigen
 

Verwandte Themen - die Größten
 Themen   Antworten   Autor   Aufrufe   Letzter Beitrag 
Keine neuen Beiträge Skifahrer will Looping fahren 145 Castillo 18652 08. Feb 2007 17:51
Castillo Letzten Beitrag anzeigen
Keine neuen Beiträge Trägheitsgesetz 87 Systemdynamiker 28687 20. Jun 2018 19:28
DrStupid Letzten Beitrag anzeigen
Keine neuen Beiträge Looping 78 gabbo123 22116 18. Jan 2008 03:13
gabbo123 Letzten Beitrag anzeigen
Keine neuen Beiträge Freier Fall und Energieerhaltung 55 Gast 27889 13. Jan 2011 22:07
planck1858 Letzten Beitrag anzeigen
Keine neuen Beiträge Energieerhaltung widerlegt? 53 Superjochen 9236 05. Dez 2022 09:16
Gast0815 Letzten Beitrag anzeigen
 

Verwandte Themen - die Beliebtesten
 Themen   Antworten   Autor   Aufrufe   Letzter Beitrag 
Keine neuen Beiträge Trägheitsgesetz 87 Systemdynamiker 28687 20. Jun 2018 19:28
DrStupid Letzten Beitrag anzeigen
Keine neuen Beiträge Freier Fall und Energieerhaltung 55 Gast 27889 13. Jan 2011 22:07
planck1858 Letzten Beitrag anzeigen
Keine neuen Beiträge Aus welcher Höhe muss ein Körper für den looping starten? 3 serverone 26370 10. Apr 2008 19:36
serverone Letzten Beitrag anzeigen
Keine neuen Beiträge Looping 78 gabbo123 22116 18. Jan 2008 03:13
gabbo123 Letzten Beitrag anzeigen
Keine neuen Beiträge Unterschied: Impulserhaltung - Energieerhaltung 8 Josy 21633 23. Feb 2011 11:15
VeryApe Letzten Beitrag anzeigen
 




 
© 2004-2021 bei Physikerboard.de | Kontakt | Jugendschutz | Nutzungsbedingungen