| Autor |
Nachricht |
St3fan85
Anmeldungsdatum: 04.05.2015
Beiträge: 18
|
 St3fan85 Verfasst am: 30. Apr 2021 13:05 Titel: Poisson Gl. durch Fouriertrafo mit Python lösen |
 |
|
Hallo,
ich bin gerade dabei mir das Programmieren mit Python beizubringen und wollte dafür die Poissongleichung mit Hilfe der diskreten Fourier-Transformation(DFT) lösen.
 = \rho(x,y))
dazu verwende ich die DFT:
Wenn ich die DFT auf die PoissonGl anwende, dann komm ich auf das Ergebnis:
^2+\left(-2\pi i \frac{l}{L_y}\right)^2} \: \hat{\rho}_{k,l})
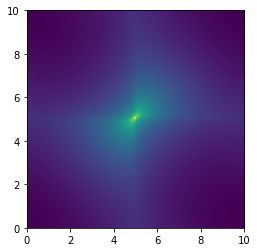
Jetzt habe ich also eine Ladungsverteilung 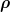 erstellt. Zum Anfang eine einzelne Ladung in der Mitte meines Feldes. Danach wurde durch Numpy eine FFT auf das Array durchgeführt und ich habe alle Werte des Transformierten Arrays mit dem Faktor von Oben geteilt. Danach wurde die inverse FFT angewendet und sollte damit die Lösung für  erhalten. Das Ergebnis habe ich als Plot hochgeladen. Man erkennt eine nicht symmetrische Verteilung für , wobei die Lösung doch Gaußglockenförmig um der Position der Ladung sein sollte.
Hat Jemand eine Idee was ich falsch gemacht habe?
Das ist der Code den ich verwende:
| Code: |
import numpy as np
import matplotlib.pyplot as plt
length = 10
steps = 100
rho = np.zeros((steps,steps))
rho[steps//2-1:steps//2,steps//2-1:steps//2] = -1
plt.imshow(rho, origin='lower', interpolation='none')
plt.show()
rho_fft = np.fft.fft2(rho)
for x in range(len(rho_fft)):
for y in range(len(rho_fft)):
if x==0 and y==0: rho_fft[x,y]=0
else:
k_sqr = (2 * np.pi * x / length)**2 + (2 * np.pi * y / length)**2
rho_fft[x,y] = -rho_fft[x,y] / k_sqr
phi = np.fft.ifft2(rho_fft)
phi_abs = np.real(phi)
plt.imshow(phi_abs,extent=(0,length,0,length ))
plt.show()
|
Vielen Dank für eure Tipps und
viele Grüße
Stefan
| Beschreibung: |
|
| Dateigröße: |
22.9 KB |
| Angeschaut: |
1338 mal |
|
Zuletzt bearbeitet von St3fan85 am 03. Mai 2021 23:51, insgesamt einmal bearbeitet |
|
 |
St3fan85
Anmeldungsdatum: 04.05.2015
Beiträge: 18
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18058
|
| TomS Verfasst am: 03. Mai 2021 08:35 Titel: |
|
|
In deiner Poisson-Gleichung fehlt ein Quadrat beim Nabla-Operator.
Zu deinem Code kann ich erst mal nichts sagen.
So wie du die Gleichung ansetzt, löst du das Problem auf einem 2-Torus bzw. der 2-dim. Ebene mit der Zusatzbedingungen periodischer Funktionen in x und y. Diese Bedingung muss auch deine Ladungsverteilung erfüllen.
Hast du das Problem mal in einer Dimension gelöst?
Ich fasse nochmal zusammen:
 = \sum_{mn}f_{mn}e^{-imx}e^{-iny})
Daraus folgt
\phi_{mn} = \rho_{mn})
und somit
 = \sum_{mn}\frac{\rho_{mn}}{(m^2 + n^2)}e^{-imx}e^{-iny})
Dabei ist zu beachten, dass konstante und lineare Funktionen in x,y durch diesen Ansatz nicht festgelegt werden, d.h. auch, dass m=0, n=0 gesondert betrachtet werden müssen.
Soweit ist jedenfalls alles gut.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18058
|
| TomS Verfasst am: 03. Mai 2021 09:19 Titel: Re: Poisson Gl. durch Fouriertrafo mit Python lösen |
|
|
| St3fan85 hat Folgendes geschrieben: |
Das ist der Code den ich verwende:
| Code: |
for x in range(len(rho_fft)):
for y in range(len(rho_fft)):
if x==0 and y==0: rho_fft[x,y]=0
else:
k_sqr = (2 * np.pi * x / length)**2 + (2 * np.pi * y / length)**2
rho_fft[x,y] = -rho_fft[x,y] / k_sqr
|
|
in deiner Formel stehen richtigerweise x, y sowie k, l; in deinem Code sehe ich dagegen
| Code: |
k_sqr = (2 * np.pi * x / length)**2 + (2 * np.pi * y / length)**2
|
kein k, l.
Ich kenne die Methode der FFT in Python nicht, aber irgendwie sieht das seltsam aus. Wieso packst du in der Schleife die Werte in ein Array in [x,y]? Du rechnest doch im k-Raum, also erwarte ich ein Array in [k,l], anschließend die Rücktrf. nach [x,y].
Aus eigener Erfahrung: verwende konsistente Bezeichner, Variablen etc. zwischen deinen Rechnungen und dem Code.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
St3fan85
Anmeldungsdatum: 04.05.2015
Beiträge: 18
|
| St3fan85 Verfasst am: 03. Mai 2021 18:10 Titel: |
|
|
Hallo,
Das Quadrat am Nabla habe ich vergessen.
Mit den Bezeichnungen hast Du natürlich vollkommen Recht, das führt nur zu Verwirrungen.
Der Code wurde allerdings auch schon verändert, damit nur numpy-Funktionen zu verwenden, um Schleifen zu vermeiden. Das bringt eine deutlich bessere Effizienz:
| Code: |
import numpy as np
import matplotlib.pyplot as plt
length = 10
steps = 100
rho = np.zeros((steps,steps))
rho[steps//2-2:steps//2+2,steps//2-2:steps//2+2] = -1
plt.imshow(rho, origin='lower', interpolation='none')
plt.show()
rho_fft = np.fft.fft2(rho)
rho_fft_shift = np.fft.fftshift(rho_fft)
plt.imshow(np.abs(rho_fft_shift))
plt.show()
kk, ll = np.meshgrid(range(steps), range(steps))
k_sqr = (2 * np.pi * kk / length) ** 2 + (2 * np.pi * ll / length) ** 2
rho_fft = np.divide(-rho_fft, k_sqr, out=np.zeros_like(rho_fft), where=k_sqr != 0)
phi = np.fft.ifft2(rho_fft)
phi_abs = np.real(phi)
plt.imshow(phi_abs,extent=(0,length,0,length ))
plt.show() |
Ich habe mir das irgendwie zu einfach vorgesellt. Ich versteh auch nicht genau wie ich die Randbedingungen mit einbringen kann.
Ich habe gelesen den Laplace-Op zu diskretisieren und dann die Fourier-Transformation anzuwenden:
 \phi \rightarrow \frac{1}{h^2} \left( \phi_{m+1,n} + \phi_{m-1,n} + \phi_{m,n+1} + \phi_{m,n-1} - 4\phi_{m,n} \right))
Das 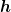 ist dabei der Abstand der diskretisierungs-Punkten.
Wenn die diskrete Fourier trafo in die `s eingesetzt wird, heben sich fast alle Terme aus den Summen auf und man kommt auf die Gleichung:
mit
Diese Methode liefert tatsächlich die richtige Lösung der Poisson-Gl. für eine Punktladung:
 https://i.ibb.co/VLDXnGt/Poisson-Lsg.png
Ich verstehe nicht was der Unterschied zwischen den beiden Varianten ist.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18058
|
| TomS Verfasst am: 03. Mai 2021 22:22 Titel: |
|
|
Jetzt musst du erst mal erklären, worauf du hinauswillst.
Willst du die kontinuierliche Poisson-Gleichung in einem endlichen Intervall bzw. kompaktifizierten Bereich lösen? Das funktioniert mittels der Fouriertransformation so wie oben von dir eingeführt und von mir nochmals bestätigt. Die Fouriertransformation erzeugt aus dem kontinuierlichen Problem im Ortsraum (x,y) ein diskretes Problem im Impulsraum (k,l). Dazu musst du keine Ableitung diskretisieren, du berechnest sie ja exakt.
Oder willst du die kontinuierliche Poisson-Gleichung im Ortsraum diskretisieren? Wozu benötigst dann noch die Fouriertransformation?
Irgendwie vermischt du jetzt beides. Warum?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
St3fan85
Anmeldungsdatum: 04.05.2015
Beiträge: 18
|
| St3fan85 Verfasst am: 03. Mai 2021 22:47 Titel: |
|
|
|
Mein Ziel ist es die Poisson-Gleichung numerisch im Ortsraum zu lösen. Dies ist, wenn ich mich nicht irre, nur möglich auf einem begrenzten Raum der diskretisiert ist. Ich habe schon einmal die Poisson-Gl. mit Dirichlet-RB mit Hilfe der Finiten-Differenzen-Methode numerisch gelöst. Da aber diese Methode rechnerisch sehr aufwendig ist und daher viel Rechenzeit braucht, wollte ich es über den Weg mit der Fourier-Transformation versuchen, da dieser als sehr effizient gilt.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18058
|
| TomS Verfasst am: 03. Mai 2021 23:18 Titel: |
|
|
| St3fan85 hat Folgendes geschrieben: | | Mein Ziel ist es die Poisson-Gleichung numerisch im Ortsraum zu lösen. Dies ist, wenn ich mich nicht irre, nur möglich auf einem begrenzten Raum der diskretisiert ist. |
Ja.
Die Bedingung des endlichen Raumes kann man durch eine geeignete Koordinatentransformation umgehen, allerdings erkauft läuft man damit in andere Schwierigkeiten.
Also bleiben wir zunächst beim endlichen Raum.
| St3fan85 hat Folgendes geschrieben: | | Da aber diese Methode rechnerisch sehr aufwendig ist und daher viel Rechenzeit braucht, wollte ich es über den Weg mit der Fourier-Transformation versuchen, da dieser als sehr effizient gilt. |
Auch gut.
Allerdings, wenn du die Fourier-Transformation nutzt, rechnest du nicht mehr im kontinuierlichen Ortsraum, stattdessen verwendest du diskrete Vektoren und Matrizen in k,l. Letztlich steht alles, was mathematisch notwendig ist, bereits da, du musst es lediglich korrekt implementieren.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18058
|
| TomS Verfasst am: 03. Mai 2021 23:58 Titel: |
|
|
Ich habe mir jetzt nochmal deinen Code angesehen. In meiner ersten Interpretation steckte ein Denkfehler, das ist jetzt klar. Abgesehen von den Zeilen, die ich mangels Python-Kenntnissen nicht ganz verstehe, sieht das doch sinnvoll aus.
Trotzdem: der Fehler steckt im Code; die Mathematik im ersten Ansatz ist ok und sinnvoll.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
St3fan85
Anmeldungsdatum: 04.05.2015
Beiträge: 18
|
| St3fan85 Verfasst am: 04. Mai 2021 13:02 Titel: |
|
|
Hallo,
ich habe herausgefunden wo das Problem liegt. Es war ein Fehler in der Verwendung der FFT Funktion.
Die FFT-Funktion gibt ein Array mit einer bestimmten Sortierung zurück:
Wenn a ein 1D Array mit n Werten ist und A=FFT(a) angewendet wird, dann gilt:
A[0] : Summe der Werte oder Null-Frequenz Term
A[1] bis A[n/2]: Positive Frequenz-Werte (aufsteigend sortiert)
A[n/2+1] bis A[n-1] Negative Frequenz-Werte (absteigend sortiert)
Dementsprechend habe ich immer bei der Division durch 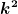 falsche Werte berechnet.
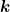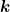Ich habe den richtigen Code angefügt. Die Berechnung der richtigen  -Werte folgt wie immer im -Raum:
Der Abstand zwischen zwei Gitterpunkten i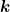m -Raum: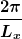 
Bei 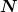 Gitterpunkten habe ich eine x-Achse erstellt im Bereich :\frac{2\pi}{L_x} N\right])
Das Selbe für die y-Achse und dann die passenden  -Werte für das 2D-Gitter Addiert und mit der Transformierten Ladungsverteilung dividiert.
Praktischer Weise gibt es einen passenden Befehl dafür in Numpy der die passenden k-Werte erstellt. Im Code habe ich beider Varianten angegeben. Von Hand und per Numpy
| Code: |
import numpy as np
import matplotlib.pyplot as plt
length = 1 # Seitenlänge des Bereichs
steps = 100 # Anzahl der Gitterpunkte
h = length/steps # Abstand zw. Gitterpunkten
rho = np.zeros((steps,steps)) # Leeres Array für Ladungsverteilung
rho[steps//2,steps//2] = -1 # Eine Ladung in die Mitte des Feldes setzen
rho_fft = np.fft.fft2(rho) # Fourier-Transformation der Ladungsverteilung
# Variante 1: Von Hand Berechnung der k_x und k_y und Sortierung
# passend für die Transformierte Ladungsverteilung
k_positiv = np.arange(0, 2*np.pi / length * steps//2, 2*np.pi / length)
k_negativ = np.arange(2*np.pi / length, 2*np.pi / length * (steps+1)//2, 2*np.pi/length)
# Zusammenfügen pos und neg k Werte in der passenden Reihenfolge
k = np.concatenate((k_positiv, np.flip(-k_negativ)), axis = None)
k_x, k_y = np.meshgrid(k, k) # kx und ky Werte für das 2D Gitter
'''
# Variante 2: Automatisiert durch Numpy
#Befehl eigentlich für Frequenzen, daher mit 2pi multiplizieren
k = 2 * np.pi * np.fft.fftfreq(steps, d=h)
k_x, k_y = np.meshgrid(k, k) # kx und ky Werte für das 2D Gitter
'''
k_sqr = k_x**2 + k_y**2 # k^2 für jeden Gitterplatz
# Division jedes Gitterplatzes mit k^2 außer bei k^2=0
rho_fft = np.divide(-rho_fft, k_sqr, out=np.zeros_like(rho_fft), where=k_sqr != 0)
phi = np.fft.ifft2(rho_fft) # Rücktransformation
phi_real = np.real(phi) # Realteil der Rücktransformation
# Darstellung des Ergebnisses
plt.imshow(phi_real,extent=(0,length,0,length ))
plt.colorbar()
plt.show()
|
Lösung:
https://i.ibb.co/1s2Hqd6/pois-lsg.png
Vielen Dank für die tolle Hilfe
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18058
|
| TomS Verfasst am: 04. Mai 2021 16:41 Titel: |
|
|
Gerne - und danke für deine Rückmeldung und die Ergebnisse.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
|
|
Registrieren
Login
FAQ
Suchen
