| Autor |
Nachricht |
Brandti
Anmeldungsdatum: 29.11.2005
Beiträge: 21
|
 Brandti Verfasst am: 19. Apr 2008 17:07 Titel: Vektorgleichung ohne Komponentendarstellung lösen Brandti Verfasst am: 19. Apr 2008 17:07 Titel: Vektorgleichung ohne Komponentendarstellung lösen |
 |
|
Hallo allerseits
Wir haben auf unserem ersten Übungsblatt für theoretische Physik folgende Aufgabe gestellt bekommen, bei der ich noch nicht mal einen sinnvollen Ansatz habe.
Da die Aufgaben davor und danach hauptsächlich mit dem Levi-Civita-Symbol und dem Kroneckersymbol zu tun haben, nehme ich an das die auch bei dieser Aufgabe sinnvoll sind.
Nun zur Aufgabe:
Lösen Sie die folgenden Gleichungen nach 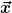 auf, ohne eine Komponentendarstellung zu benutzen. Unter welcher Bedingung ist die Lösung eindeutig? auf, ohne eine Komponentendarstellung zu benutzen. Unter welcher Bedingung ist die Lösung eindeutig?
a) \vec{b})
b) +(\vec{x},\vec{b})\vec{c}=\vec{d})
Für ein wenig Hilfe wäre ich dankbar, vorallem, da ich alle anderen Aufgaben fertig habe und nur bei dieser keine Ahnung habe.
MfG Brandti |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 19. Apr 2008 17:27 Titel: dermarkus Verfasst am: 19. Apr 2008 17:27 Titel: |
 |
|
Wenn da steht, man soll das hier ohne Komonentendarstellung machen, dann würde ich sagen, braucht man hier auch keinen Levi-Civita-Tensor und kein Kronecker-Symbol.
Hast du schon eine anschauliche Vorstellung davon, was Skalarprodukt und Kreuzprodukt von Vektoren bedeuten? Magst du dir mal konkret aufmalen, welche Zusammenhänge zwischen Vektoren in diesen Gleichungen dargestellt sind? Erkennst du damit bereits Zusammenhänge?
Oder kennt ihr bereits fertige Rechenregeln für den Umgang mit Vektorprodukten, etc., wie zum Beispiel die "bac-cab" - Regel, die ihr euch vielleicht gerade in den anderen Übungsaufgaben hergeleitet habt? |
|
 |
Brandti
Anmeldungsdatum: 29.11.2005
Beiträge: 21
|
 Brandti Verfasst am: 19. Apr 2008 18:09 Titel: Brandti Verfasst am: 19. Apr 2008 18:09 Titel: |
 |
|
Also bac-cab haben wir in der Aufgabe vorher bewiesen.
Dann gibt das in b):
-\vec{x}(\vec{a},\vec{b})+\vec{c}(\vec{x},\vec{b})=\vec{d})
außerdem haben wir noch
=(\vec{b},\vec{c}\times\vec{a})=(\vec{c},\vec{a}\times\vec{b}))
bewiesen.
Aber nach o.g. Schritt komme ich bei der b) nicht mehr weiter, bei der a) sehe ich für diese Regeln erstmal keine Anwendungsmöglichkeit.
Was Skalarprodukt und Kreuzprodukt bedeuten, weiß ich natürlich.
MfG Brandti |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 19. Apr 2008 18:34 Titel: dermarkus Verfasst am: 19. Apr 2008 18:34 Titel: |
 |
|
Da habe ich zwei Vermutungen für Wege, die (eventuell auch in Kombination miteinander) für dich zum Erfolg führen könnten:
a) Du kratzt alle, aber auch alle Vektorbeziehungen aus allen Übungsaufgaben zusammen, die ihr zu so etwas bisher gerechnet habt, und versuchst damit, so gut es geht, umzuformen.
b) Du machst dir das ganze zu gut wie möglich auch grafisch klar. (Ich selbst bin immer wieder verblüfft, wie einfach solche kompliziert oder abstrakt scheinenden Vektorgleichungen werden können, wenn man Wege findet, sie sich grafisch und geometrisch darzustellen.) Angefangen zum Beispiel mit dem, was ein Skalarprodukt mit der Projektion des einen Vektors auf die Richtung des anderen zu tun hat. Über das, was ein Spatprodukt mit dem Volumen eines von diesen drei Vektoren aufgespannten Körpers zu tun hat. etc., etc.
//edit: Tippfehler beseitigt
Zuletzt bearbeitet von dermarkus am 01. Nov 2008 00:24, insgesamt einmal bearbeitet |
|
 |
Thomas
Administrator
Anmeldungsdatum: 20.02.2004
Beiträge: 701
|
 Thomas Verfasst am: 21. Apr 2008 14:12 Titel: Thomas Verfasst am: 21. Apr 2008 14:12 Titel: |
 |
|
Probier mal, das Skalarprodukt mit einer nx1 Matrix zu schreiben.
Konkret: =x^Ty ) |
|
 |
Thomas
Administrator
Anmeldungsdatum: 20.02.2004
Beiträge: 701
|
 Thomas Verfasst am: 21. Apr 2008 20:46 Titel: Thomas Verfasst am: 21. Apr 2008 20:46 Titel: |
 |
|
Weitere Möglichkeit:
Bei der a) Skalardurchmultiplizieren mit 
+(\vec{a},\vec{c})=(\vec{x},\vec{c})(\vec{b},\vec{c}))
Dann kann man nach dem Skalarprodukt auflösen und weitermachen. |
|
 |
physikanfaenger
Anmeldungsdatum: 31.10.2008
Beiträge: 8
|
 physikanfaenger Verfasst am: 31. Okt 2008 21:05 Titel: physikanfaenger Verfasst am: 31. Okt 2008 21:05 Titel: |
 |
|
Sorry, dass ich den Thread nochmal nach oben hole, aber ich habe heute (leider) dieselbe Aufgabe in der Uni bekommen und bin gerade total verzweifelt, weil es erst der erste Übungszettel ist und ich dennoch schon ziemliche Probleme habe. 
Nun zur Aufgabe:
Ich bin sie heute mal angegangen und bin auf folgenden Rechenweg gekommen, welcher jedoch falsch ist. Dies weiß ich, weil ich nämlich probeweise Zahlenwerte eingesetzt habe und die Gleichung nicht mehr gestimmt hat.
x + a = (x*c)*b | * c
(x*c)+(a*c) = (x*c)*(b*c) | - (x*c)
(a*c) = (x*c)*(b*c) - (x*c) | auf der rechten Seite (x*c) ausklammern
(a*c) = (x*c)*((b*c) - 1) | : ((b*c) - 1)
(a*c) / ((b*c) - 1) = x*c | : c
a / ((b*c) - 1) = x
(rechts neben dem | stehen die Rechenschritte)
Kann zufällig jemand von euch den Fehler erkennen und mir weiterhelfen?
Danke |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 31. Okt 2008 21:29 Titel: dermarkus Verfasst am: 31. Okt 2008 21:29 Titel: |
 |
|
Ich kann schon mal sagen, wo der Umformfehler ist:
Was du als x, a, b und c hinschreibst, sind ja keine Zahlen, sondern Vektoren. Du meinst also sicher jeweils 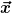 , , 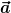 , ,  und und  . .
"Durch einen Vektor teilen", wie du es offenbar im Schritt von der vorletzten zur letzten Rechenzeile tun wolltest, geht aber nicht. Dieser Schritt ist keine Äquivalenzumformung.
Denn in der vorletzten Zeile steht ja lediglich die Information, dass die Projektion des Vektors 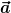 auf die Richtung des Vektors auf die Richtung des Vektors  (dividiert durch die Zahl (dividiert durch die Zahl ) ) gleich der Projektion des Vektors ) gleich der Projektion des Vektors 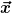 auf die Richtung des Vektors auf die Richtung des Vektors  ist. ist. |
|
 |
physikanfaenger
Anmeldungsdatum: 31.10.2008
Beiträge: 8
|
 physikanfaenger Verfasst am: 31. Okt 2008 23:35 Titel: physikanfaenger Verfasst am: 31. Okt 2008 23:35 Titel: |
 |
|
Danke für die schnelle Antwort! 
Ja, also die Sache mit der Projektion kann ich so einigermaßen nachvollziehen. Ich habe bloß gedacht, dass das Teilen durch den Vektor c, dennoch möglich sein sollte, da das Gegenteil, also die Multiplikation mit c, ja auch möglich war bzw. ist. Welche Möglichkeit gibt es denn noch, um c zu eliminieren?
bist du dir sicher, dass der rest in Ordnung ist? Ich habe den Fehler nämlich bei dem Ausklammern von (x*c) vermutet. |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 31. Okt 2008 23:55 Titel: dermarkus Verfasst am: 31. Okt 2008 23:55 Titel: |
 |
|
Der Rest davor ist insofern in Ordnung, als dass da in jeder Zeile wahre Aussagen stehen. Denn wenn die vorangegangenen Zeilen richtig sind, dann sind die folgenden richtig (bis vor der versuchten Division durch den Vektor).
Bei der Multiplikation mit dem Vektor  hast du allerdings wohl Informationen verloren, da es viele Möglichkeiten für ursprüngliche Vektoren geben könnte, die im Skalarprodukt dieselbe Projektion auf die Richtung von hast du allerdings wohl Informationen verloren, da es viele Möglichkeiten für ursprüngliche Vektoren geben könnte, die im Skalarprodukt dieselbe Projektion auf die Richtung von  multipliziert mit dem Betrag von multipliziert mit dem Betrag von  ergeben können. ergeben können.
Also sind nicht alle Vektoren, die die nachfolgenden Gleichungen erfüllen, automatisch auch Lösungen der Ausgangsgleichung.
Da ich auch noch nicht weiß, wie ich das am elegantesten nach 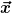 umformen würde, würde ich da wohl erstmal anfangen, mir Pfeile zu malen und damit zu überlegen, welche Lösungen es geben kann. (Oder mal auf dem Übungsblatt schauen, welche anderen Beziehungen für Vektorrechnung da schon mit draufstehen, die man vielleicht noch mit verwenden könnte). umformen würde, würde ich da wohl erstmal anfangen, mir Pfeile zu malen und damit zu überlegen, welche Lösungen es geben kann. (Oder mal auf dem Übungsblatt schauen, welche anderen Beziehungen für Vektorrechnung da schon mit draufstehen, die man vielleicht noch mit verwenden könnte).
Zum Beispiel, wenn ich mir den Vektor  aufmale und eine Gerade hindurchzeichne, dann muss man mit den zwei Pfeilen aufmale und eine Gerade hindurchzeichne, dann muss man mit den zwei Pfeilen 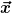 und und 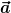 hintereinandergehängt, ausgehend von einem Punkt auf dieser Geraden wieder auf dieser Geraden landen. Denn die Klammer vor dem hintereinandergehängt, ausgehend von einem Punkt auf dieser Geraden wieder auf dieser Geraden landen. Denn die Klammer vor dem  in der Anfangsgleichung ist nur eine Zahl vor dem Vektor. in der Anfangsgleichung ist nur eine Zahl vor dem Vektor.
Zuletzt bearbeitet von dermarkus am 01. Nov 2008 00:09, insgesamt einmal bearbeitet |
|
 |
physikanfaenger
Anmeldungsdatum: 31.10.2008
Beiträge: 8
|
 physikanfaenger Verfasst am: 01. Nov 2008 00:04 Titel: physikanfaenger Verfasst am: 01. Nov 2008 00:04 Titel: |
 |
|
Nun ja, die Aufgabenstellung hat Brandti ja bereits im Eingangpost beschrieben und sie lautet:
Lösen Sie die folgenden Gleichungen nach auf, ohne eine Komponentendarstellung zu benutzen. Unter welcher Bedingung ist die Lösung eindeutig?
Mehr Infos/Hinweise stehen da leider nicht. in der Vorlesung hatten wir auch nur die gewöhnlichen Formeln, also die Definition des Skalarprodukts, a*b =|a||b|cos phi, usw. |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 01. Nov 2008 00:32 Titel: dermarkus Verfasst am: 01. Nov 2008 00:32 Titel: |
 |
|
| physikanfaenger hat Folgendes geschrieben: |
Mehr Infos/Hinweise stehen da leider nicht. |
Ja, klar, das ist ja auch eine Aufgabe fürs Studium  Da darf und soll man sicher auch selbst intensiv probieren mit den Mitteln, die einem selbst einfallen und den Mitteln, die man zum Beispiel durch Nachschlagen finden kann. Da darf und soll man sicher auch selbst intensiv probieren mit den Mitteln, die einem selbst einfallen und den Mitteln, die man zum Beispiel durch Nachschlagen finden kann.
Ob in den anderen Aufgaben deines Übungszettels Beziehungen vorkommen, die für diese Aufgabe nützlich sein könnten, weiß ich nicht, weil ich den Zettel nicht im ganzen kenne.
Wie weit kommst du, wenn du mal anfängst, durch grafisches Aufzeichnen der Vektoren und der Beziehungen, die du über sie herausfinden kannst, Informationen über diese Vektoren zusammenzustellen?
Man könnte zum Beispiel auch mal mit  multiplizieren und das, was man damit erhält, sich grafisch veranschaulichen, um weitere Informationen über diese Gleichung zu sammeln. multiplizieren und das, was man damit erhält, sich grafisch veranschaulichen, um weitere Informationen über diese Gleichung zu sammeln. |
|
 |
physikanfaenger
Anmeldungsdatum: 31.10.2008
Beiträge: 8
|
 physikanfaenger Verfasst am: 01. Nov 2008 09:34 Titel: physikanfaenger Verfasst am: 01. Nov 2008 09:34 Titel: |
 |
|
| dermarkus hat Folgendes geschrieben: | Ja, klar, das ist ja auch eine Aufgabe fürs Studium  Da darf und soll man sicher auch selbst intensiv probieren mit den Mitteln, die einem selbst einfallen und den Mitteln, die man zum Beispiel durch Nachschlagen finden kann. Da darf und soll man sicher auch selbst intensiv probieren mit den Mitteln, die einem selbst einfallen und den Mitteln, die man zum Beispiel durch Nachschlagen finden kann. |
Dagegen habe ich prinzipiell ja auch nichts, nur leider muss man durchschnittlich 70% der Punkte erreichen, um für die Klausur zugelassen zu werden und deshalb lastet ein ziemlicher Druck auf mir. 
| dermarkus hat Folgendes geschrieben: | | Ob in den anderen Aufgaben deines Übungszettels Beziehungen vorkommen, die für diese Aufgabe nützlich sein könnten, weiß ich nicht, weil ich den Zettel nicht im ganzen kenne. |
Ne, leider ist da wohl nix nützliches. Die anderen Aufgaben handeln nämlich von der Schwarz'schen Ungleichung und der Dreiecksungleichung.
| dermarkus hat Folgendes geschrieben: | Wie weit kommst du, wenn du mal anfängst, durch grafisches Aufzeichnen der Vektoren und der Beziehungen, die du über sie herausfinden kannst, Informationen über diese Vektoren zusammenzustellen?
Man könnte zum Beispiel auch mal mit  multiplizieren und das, was man damit erhält, sich grafisch veranschaulichen, um weitere Informationen über diese Gleichung zu sammeln. multiplizieren und das, was man damit erhält, sich grafisch veranschaulichen, um weitere Informationen über diese Gleichung zu sammeln. |
Das habe ich auch schon probiert, aber leider habe ich nichts für die Aufgabe relevantes herausbekommen können. Vielleicht habe ich ja auch irgendetwas wichtiges übersehen!? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 01. Nov 2008 12:15 Titel: dermarkus Verfasst am: 01. Nov 2008 12:15 Titel: |
 |
|
Vielleicht hast du dir das, was beim Multiplizieren mit  als Gleichung herauskommt, nur noch nicht anschaulich genug vor Augen geführt. als Gleichung herauskommt, nur noch nicht anschaulich genug vor Augen geführt.
Hast du auch zum Beispiel schon mal versucht, die Anfangsgleichung mit 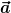 durchzumultiplizieren? Welche Gleichung bekommst du damit, und welche Information gibt dir das über den Vektor durchzumultiplizieren? Welche Gleichung bekommst du damit, und welche Information gibt dir das über den Vektor 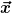 ? ?
Magst du mal die vorletzte Zeile deiner Rechnung von oben in exakterer Schreibweise hier aufschreiben? Also überall dort wirklich einen Pfeil über den Buchstaben machen, wo du einen Vektor meinst? (Ein normal getippter Buchstabe ohne Pfeil drüber meint nicht den Vektor, sondern den Betrag des zugehörigen Vektors.)
Und dann mal sagen, welche Information du damit über das Skalarprodukt von 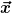 und und  gewonnen hast? Hat dieses Teilergebnis eine grafische Bedeutung, mit Hilfe derer du diese gewonnene Teilinformation leichter verstehen und in Kombination mit anderen Informationen weiterverwenden kannst? gewonnen hast? Hat dieses Teilergebnis eine grafische Bedeutung, mit Hilfe derer du diese gewonnene Teilinformation leichter verstehen und in Kombination mit anderen Informationen weiterverwenden kannst? |
|
 |
physikanfaenger
Anmeldungsdatum: 31.10.2008
Beiträge: 8
|
 physikanfaenger Verfasst am: 01. Nov 2008 14:22 Titel: physikanfaenger Verfasst am: 01. Nov 2008 14:22 Titel: |
 |
|
| dermarkus hat Folgendes geschrieben: | Vielleicht hast du dir das, was beim Multiplizieren mit  als Gleichung herauskommt, nur noch nicht anschaulich genug vor Augen geführt. als Gleichung herauskommt, nur noch nicht anschaulich genug vor Augen geführt. |
Doch das habe ich natürlich probiert, aber weil keine Werte dabei waren fiel es mir schwer, nützliche Infos aus der Zeichung zu holen.
| Zitat: | Hast du auch zum Beispiel schon mal versucht, die Anfangsgleichung mit 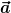 durchzumultiplizieren? Welche Gleichung bekommst du damit, und welche Information gibt dir das über den Vektor durchzumultiplizieren? Welche Gleichung bekommst du damit, und welche Information gibt dir das über den Vektor 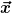 ? ? |
Ich habe bereits alle möglichen Multiplikationen mit der Gleichung  \cdot \vec b) ausprobiert, aber leider wurde das Ergebnis bei den Multiplikationen mit ausprobiert, aber leider wurde das Ergebnis bei den Multiplikationen mit  nur noch größer und unübersichtlicher und letztendlich konnte ich dann nicht mal mehr nach nur noch größer und unübersichtlicher und letztendlich konnte ich dann nicht mal mehr nach 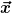 auflösen. auflösen.
| Zitat: | | Magst du mal die vorletzte Zeile deiner Rechnung von oben in exakterer Schreibweise hier aufschreiben? Also überall dort wirklich einen Pfeil über den Buchstaben machen, wo du einen Vektor meinst? (Ein normal getippter Buchstabe ohne Pfeil drüber meint nicht den Vektor, sondern den Betrag des zugehörigen Vektors.) |
 - 1} = \vec x \cdot \vec c)
| Zitat: | Und dann mal sagen, welche Information du damit über das Skalarprodukt von 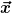 und und  gewonnen hast? Hat dieses Teilergebnis eine grafische Bedeutung, mit Hilfe derer du diese gewonnene Teilinformation leichter verstehen und in Kombination mit anderen Informationen weiterverwenden kannst? gewonnen hast? Hat dieses Teilergebnis eine grafische Bedeutung, mit Hilfe derer du diese gewonnene Teilinformation leichter verstehen und in Kombination mit anderen Informationen weiterverwenden kannst? |
Also wenn ich die Bedeutung des Skalarprodukts richtig verstanden habe, dann bedeutet die vorletzte Zeile, dass die Projektion von 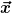 auf auf  genauso groß bzw. lang ist wie der Betrag der Projektion von genauso groß bzw. lang ist wie der Betrag der Projektion von 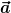 auf auf  geteilt durch den Betrag der Projektion von geteilt durch den Betrag der Projektion von  auf auf  - 1. Leider hilft mir das momentan noch nicht wirklich weiter. Ich werde mir aber gleich nochmal Gedanken darüber machen und vielleicht kommt dann der Geistesblitz!? - 1. Leider hilft mir das momentan noch nicht wirklich weiter. Ich werde mir aber gleich nochmal Gedanken darüber machen und vielleicht kommt dann der Geistesblitz!?  |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 01. Nov 2008 15:21 Titel: dermarkus Verfasst am: 01. Nov 2008 15:21 Titel: |
 |
|
| physikanfaenger hat Folgendes geschrieben: |
 - 1} = \vec x \cdot \vec c)
|
Einverstanden 
Hast du in der Schule in Mathe schon mit dreidimensionalen Vektoren gerechnet? Und zum Beispiel Gleichungen für Kugeln oder Ebenen oder Geraden in Vektorschreibweise aufgestellt und verwendet? Erinnert dich diese Gleichung hier an etwas, das du von daher vielleicht schon kennst?
Wenn der Vektor 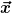 ein Ortsvektor wäre, der im Koordinatenursprung startet, was für ein Gebilde wäre dann die Menge aller Punkte ein Ortsvektor wäre, der im Koordinatenursprung startet, was für ein Gebilde wäre dann die Menge aller Punkte 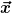 , die diese Gleichung erfüllen? , die diese Gleichung erfüllen?
| Zitat: |
Also wenn ich die Bedeutung des Skalarprodukts richtig verstanden habe, dann bedeutet die vorletzte Zeile, dass die Projektion von 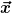 auf auf  genauso groß bzw. lang ist wie der Betrag der Projektion von genauso groß bzw. lang ist wie der Betrag der Projektion von 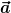 auf auf  geteilt durch den Betrag der Projektion von geteilt durch den Betrag der Projektion von  auf auf  - 1. - 1. |
So hatte ich das oben versucht, in kurzen Worten auszudrücken, ja.
Das Skalarprodukt selbst ist ja noch genauer gesagt die Zahl, die man bekommt, wenn man die Länge der Projektion des einen Vektors auf den anderen mit der Länge des anderen Vektors multipliziert.
Was das bedeutet, und was man damit in der Vektorrechnung zum Beispiel so alles machen kann, hast du bestimmt schon mal in der Schule kennengelernt. Hilft dir das ein bisschen beim anschaulichen Vorstellen dessen, was deine Gleichungen sagen? |
|
 |
physikanfaenger
Anmeldungsdatum: 31.10.2008
Beiträge: 8
|
 physikanfaenger Verfasst am: 01. Nov 2008 15:37 Titel: physikanfaenger Verfasst am: 01. Nov 2008 15:37 Titel: |
 |
|
| dermarkus hat Folgendes geschrieben: | Einverstanden 
Hast du in der Schule in Mathe schon mit dreidimensionalen Vektoren gerechnet? Und zum Beispiel Gleichungen für Kugeln oder Ebenen oder Geraden in Vektorschreibweise aufgestellt und verwendet? Erinnert dich diese Gleichung hier an etwas, das du von daher vielleicht schon kennst?
Wenn der Vektor 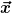 ein Ortsvektor wäre, der im Koordinatenursprung startet, was für ein Gebilde wäre dann die Menge aller Punkte ein Ortsvektor wäre, der im Koordinatenursprung startet, was für ein Gebilde wäre dann die Menge aller Punkte 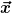 , die diese Gleichung erfüllen? , die diese Gleichung erfüllen? |
Ich hatte das Thema Vektorrechnung leider nie in der Schule (Zentralabitur  ). Alles was ich darüber weiss, habe ich mir in den letzten drei bis vier Wochen selbst beigebracht. ). Alles was ich darüber weiss, habe ich mir in den letzten drei bis vier Wochen selbst beigebracht.
Ich würde deshalb einfach mal auf eine Ebene tippen.  |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 01. Nov 2008 15:44 Titel: dermarkus Verfasst am: 01. Nov 2008 15:44 Titel: |
 |
|
Ist dein Tipp eher geraten oder kannst du ihn mathematisch begründen?
Hast du in den letzten vier Wochen zum Beispiel schon mal etwas von einer Hesse'schen Normalenform gehört? |
|
 |
physikanfaenger
Anmeldungsdatum: 31.10.2008
Beiträge: 8
|
 physikanfaenger Verfasst am: 01. Nov 2008 15:48 Titel: physikanfaenger Verfasst am: 01. Nov 2008 15:48 Titel: |
 |
|
| dermarkus hat Folgendes geschrieben: | | Ist dein Tipp eher geraten oder kannst du ihn mathematisch begründen? |
Eher geraten. Sorry, aber ich bin noch ein Anfänger auf diesem Gebiet.
| Zitat: | | Hast du in den letzten vier Wochen zum Beispiel schon mal etwas von einer Hesse'schen Normalenform gehört? |
Na ja, indirekt: Mein Mathe-Prof hat erwähnt, dass wir das irgendwann im Laufe des Semesters machen werden und es nicht klausurrelevant sein wird.
 |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 01. Nov 2008 16:12 Titel: dermarkus Verfasst am: 01. Nov 2008 16:12 Titel: |
 |
|
Das hat er sicher nur auf seine Klausur für die Mathevorlesung bezogen.
Wenn du dir das mal anschauen möchtest und dabei findest, dass dir das für das Verständnis der Aufgabe hier weiterhilft, dann spricht nicht dagegen, dass du so etwas hier verwendest. (Viele Studienanfänger kennen so etwas einfach schon aus der Schule.)
Wenn du dir das mit den Vektoren hingegen lieber selber überlegen und intensivem "Umformen probieren" machen möchtest und damit auch schon zum Ziel kommen solltest, spricht auch da nichts dagegen.
Magst du mal versuchen, dich mit meinen Tipps neu an der Sache zu versuchen? Wie sieht die Punktmenge für die Gleichung von eben (deine Vermutung bisher "irgendeine Ebene?") genauer aus?
Welche Punktmengen erhältst du außerdem aus den Gleichungen, die du durch Multiplizieren mit den anderen Vektoren erhalten hast? |
|
 |
physikanfaenger
Anmeldungsdatum: 31.10.2008
Beiträge: 8
|
 physikanfaenger Verfasst am: 01. Nov 2008 18:05 Titel: physikanfaenger Verfasst am: 01. Nov 2008 18:05 Titel: |
 |
|
Ach, ich gebe die Sache für heute auf und widme mich den anderen Fächern, die ich habe. Ich werde es in den nächsten Tagen noch mal probieren und vielleicht finde ich dann ja etwas neues heraus.
Dennoch danke ich dir sehr für deine Hilfe, denn immerhin habe ich hier und heute nochmals eine Menge zu diesem Thema dazugelernt und das ist ja auch schon ganz gut!  |
|
 |
|


















 Da darf und soll man sicher auch selbst intensiv probieren mit den Mitteln, die einem selbst einfallen und den Mitteln, die man zum Beispiel durch Nachschlagen finden kann.
Da darf und soll man sicher auch selbst intensiv probieren mit den Mitteln, die einem selbst einfallen und den Mitteln, die man zum Beispiel durch Nachschlagen finden kann.

 ). Alles was ich darüber weiss, habe ich mir in den letzten drei bis vier Wochen selbst beigebracht.
). Alles was ich darüber weiss, habe ich mir in den letzten drei bis vier Wochen selbst beigebracht.
