| Autor |
Nachricht |
Lagrangemechaniker
Gast
|
 Lagrangemechaniker Verfasst am: 30. Mai 2020 23:16 Titel: Lagrange-Funktion eines Teilchens Lagrangemechaniker Verfasst am: 30. Mai 2020 23:16 Titel: Lagrange-Funktion eines Teilchens |
 |
|
Meine Frage:
Hallo, ich habe momentan eine Schwierigkeit folgenden Sachverhalt zu verstehen:
"Da sich die Bewegungsgleichungen bei Transformation von einem Intertialsystem in ein anderes Inertialsystem nicht ändern, kann die Lagrange-Funktion nicht explizit vom Radiusvektor 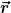 abhängen" abhängen"
Näher begründet wird das leider nirgendwo. Würde mich freuen wenn mir das jemand erklären bzw. mathematisch beweisen kann.
Meine Ideen:
Etwas anders formuliert läuft es glaube ich auf folgende Äquivalenz hinaus; Sei T die Transformation welche mein System um einen konstanten Vektor  verschiebt, also verschiebt, also  , dann gilt: , dann gilt:
Die Lagrange-Funktion ist invariant unter T  Die Bewegunsgleichungen bzw. die Lagrange-Gleichungen sind invariant unter T. Die Bewegunsgleichungen bzw. die Lagrange-Gleichungen sind invariant unter T.
"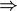 " ist mir dabei auch klar, aber " " ist mir dabei auch klar, aber " " nicht. " nicht. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 01. Jun 2020 13:19 Titel: Re: Lagrange-Funktion eines Teilchens index_razor Verfasst am: 01. Jun 2020 13:19 Titel: Re: Lagrange-Funktion eines Teilchens |
 |
|
| Lagrangemechaniker hat Folgendes geschrieben: |
"Da sich die Bewegungsgleichungen bei Transformation von einem Intertialsystem in ein anderes Inertialsystem nicht ändern, kann die Lagrange-Funktion nicht explizit vom Radiusvektor 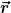 abhängen" abhängen"
[...]
Meine Ideen:
Etwas anders formuliert läuft es glaube ich auf folgende Äquivalenz hinaus; Sei T die Transformation welche mein System um einen konstanten Vektor  verschiebt, also verschiebt, also  , dann gilt: , dann gilt:
Die Lagrange-Funktion ist invariant unter T  Die Bewegunsgleichungen bzw. die Lagrange-Gleichungen sind invariant unter T. Die Bewegunsgleichungen bzw. die Lagrange-Gleichungen sind invariant unter T.
"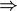 " ist mir dabei auch klar, aber " " ist mir dabei auch klar, aber " " nicht. " nicht. |
Die Umkehrung gilt doch auch nicht. Die Bewegungsgleichungen

sind translationsinvariant, folgen aber aus der Lagrangefunktion

die explizit von 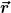 abhängt. Ich vermute in der zitierten Aussage sind eigentlich Symmetrien der Wirkung gemeint (im engeren Sinne abhängt. Ich vermute in der zitierten Aussage sind eigentlich Symmetrien der Wirkung gemeint (im engeren Sinne  ), nicht lediglich Symmetrien der Bewegungsgleichungen. Eine solche liegt in meinem Beispiel nicht vor, da ja ), nicht lediglich Symmetrien der Bewegungsgleichungen. Eine solche liegt in meinem Beispiel nicht vor, da ja
.)
(Im Hinblick auf das Noether-Theorem definiert man Symmetrien der Wirkung ja oft im weiteren Sinne als Transformationen, die die Wirkung nur um Randterme ändern. Eine solche liegt hier natürlich trotzdem vor, aber sie erfordert eben nicht die r-Unabhängigkeit von L.) |
|
 |
Lagrangemechaniker
Gast
|
 Lagrangemechaniker Verfasst am: 03. Jun 2020 20:05 Titel: Lagrangemechaniker Verfasst am: 03. Jun 2020 20:05 Titel: |
 |
|
|
Es tut mir Leid, ich hatte mich in meinem Ursprungstext verlesen und ein wichtiges kleines Wort komplett übersehen. Es soll um ein freies Teilchen in einem Inertialsystem gehen, also ohne Wechselwirkung. Dennoch verstehe ich auch unter solchen Umständen nicht ganz, dass dann die Lagrange-Funktion unabhängig vom Radiusvektor sein muss. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 04. Jun 2020 10:09 Titel: index_razor Verfasst am: 04. Jun 2020 10:09 Titel: |
 |
|
| Lagrangemechaniker hat Folgendes geschrieben: | | Es tut mir Leid, ich hatte mich in meinem Ursprungstext verlesen und ein wichtiges kleines Wort komplett übersehen. Es soll um ein freies Teilchen in einem Inertialsystem gehen, also ohne Wechselwirkung. Dennoch verstehe ich auch unter solchen Umständen nicht ganz, dass dann die Lagrange-Funktion unabhängig vom Radiusvektor sein muss. |
Was bedeutet denn "ohne Wechselwirkung"? Die Lagrangegleichungen für ein Teilchen lauten

Der "Wechselwirkungsterm" steht auf der rechten Seite. Wenn "ohne Wechselwirkung" bedeuten soll, daß er verschwindet, muß L offenbar unabhängig von r sein. Wofür benötigt man dann noch irgendeine Invarianz?
Woher stammt das Zitat denn? Und in welchem Kontext steht es? |
|
 |
Lagrangemechaniker
Anmeldungsdatum: 04.06.2020
Beiträge: 4
|
 Lagrangemechaniker Verfasst am: 04. Jun 2020 16:54 Titel: Lagrangemechaniker Verfasst am: 04. Jun 2020 16:54 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: |
Was bedeutet denn "ohne Wechselwirkung"?
|
Ich dachte das sei einfach die Definition für "freies Teilchen".
| index_razor hat Folgendes geschrieben: |

Der "Wechselwirkungsterm" steht auf der rechten Seite. Wenn "ohne Wechselwirkung" bedeuten soll, daß er verschwindet, muß L offenbar unabhängig von r sein.
|
Okay, das kann ich schon eher verstehen, aber ich bin mir nicht ganz sicher warum der rechte Term der "Wechselwirkungsterm" sein soll. Ich vermute mal weil er allgemein nur von  abhängen kann. (Also wenn die q's die generalisierten Koordinaten darstellen und t die zeit) abhängen kann. (Also wenn die q's die generalisierten Koordinaten darstellen und t die zeit)
| index_razor hat Folgendes geschrieben: |
Wofür benötigt man dann noch irgendeine Invarianz?
Woher stammt das Zitat denn? Und in welchem Kontext steht es?
|
https://www.maths.tcd.ie/~frolovs/AdvMech/Notes_Lagrangian_Mechanics.pdf
Das ist kein richtiges Zitat gewesen, aber ich bin mir eigentlich sicher, dass es den Inhalt von diesem Text ab Seite 15 "1.3 Lagrangians of various systems" bis zum Ende von Seite 16 (wo es dann auch um ein einziges Teilchen geht), zusammenfasst.
Beachte übrigens folgende Abkürzungen welche in dem Text vorgenommen wurden: eom = equations of motion, dof = degrees of freedom |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 05. Jun 2020 17:17 Titel: index_razor Verfasst am: 05. Jun 2020 17:17 Titel: |
 |
|
| Lagrangemechaniker hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: |
Was bedeutet denn "ohne Wechselwirkung"?
|
Ich dachte das sei einfach die Definition für "freies Teilchen".
|
Die Frage ist, was daraus für die Lagrangegleichungen folgt. Ansonsten hilft diese Definition nicht weiter.
| Zitat: |
| index_razor hat Folgendes geschrieben: |

Der "Wechselwirkungsterm" steht auf der rechten Seite. Wenn "ohne Wechselwirkung" bedeuten soll, daß er verschwindet, muß L offenbar unabhängig von r sein.
|
Okay, das kann ich schon eher verstehen, aber ich bin mir nicht ganz sicher warum der rechte Term der "Wechselwirkungsterm" sein soll. Ich vermute mal weil er allgemein nur von  abhängen kann. (Also wenn die q's die generalisierten Koordinaten darstellen und t die zeit) abhängen kann. (Also wenn die q's die generalisierten Koordinaten darstellen und t die zeit)
|
Weil z.B. die Lagragegleichungen für ein einzelnes Teilchen ) lauten, mit lauten, mit  . Das Argument kommt dir sicher zirkulär vor. Und das ist es auch. Man kann aus Eigenschaften der Bewegungsgleichungen allein nur sehr schwache Schlußfolgerungen über L ziehen. Das liegt einfach daran, daß L durch die Lagrangegleichungen höchstens bis auf eine totale Zeitableitung eindeutig bestimmt wird. Deshalb wird es keine strenge Herleitung für die gewünschte Form . Das Argument kommt dir sicher zirkulär vor. Und das ist es auch. Man kann aus Eigenschaften der Bewegungsgleichungen allein nur sehr schwache Schlußfolgerungen über L ziehen. Das liegt einfach daran, daß L durch die Lagrangegleichungen höchstens bis auf eine totale Zeitableitung eindeutig bestimmt wird. Deshalb wird es keine strenge Herleitung für die gewünschte Form  geben, die allein auf der Invarianz der Bewegungsgleichungen aufbaut. geben, die allein auf der Invarianz der Bewegungsgleichungen aufbaut.
Will man L festlegen, dann muß man stärkere Voraussetzungen machen, z.B., wie von mir vorgeschlagen, daß Translationen die Wirkung selbst invariant lassen. Das ist natürlich keine triviale Annahme und das Argument wird dadurch etwas zirkulär.
| Zitat: |
| index_razor hat Folgendes geschrieben: |
Wofür benötigt man dann noch irgendeine Invarianz?
Woher stammt das Zitat denn? Und in welchem Kontext steht es?
|
https://www.maths.tcd.ie/~frolovs/AdvMech/Notes_Lagrangian_Mechanics.pdf
Das ist kein richtiges Zitat gewesen, aber ich bin mir eigentlich sicher, dass es den Inhalt von diesem Text ab Seite 15 "1.3 Lagrangians of various systems" bis zum Ende von Seite 16 (wo es dann auch um ein einziges Teilchen geht), zusammenfasst.
|
Ja, da stimme ich dir zu. Wie mein Gegenbeispiel allerdings zeigt, ist die Behauptung auf S. 15 falsch. Im allgemeinen folgt aus der Invarianz der Lagrangegleichungen nur, daß sich die Lagrangefunktion um höchstens eine totale Zeitableitung ändert, d.h.
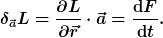
Daß nicht unbedingt F=const. sein muß, wird in dem Skript anscheinend übersehen. Insbesondere verletzt ein homogenes Kraftfeld natürlich nicht die Homogenität des Raumes. Es verletzt aber die Isotropie. Die wird ja später ohnehin verwendet.
Wenn es also nur darum geht, zu zeigen, daß man L so wählen kann, daß es unabhängig von r ist, dann reichen zumindest Translations-, Rotations- und Galileiinvarianz der Bewegungsgleichungen aus.
Wenn man davon ausgeht, daß sich die Lagrangegleichungen für ein einzelnes Teilchen auf die Form
.)
bringen lassen, kann man folgendermaßen argumentieren. Invarianz dieser Gleichung unter Raumtranslationen bedeutet, daß 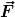 unabhängig von unabhängig von 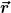 ist, denn die linke Seite ist manifest invariant und die rechte Seite nur wenn ist, denn die linke Seite ist manifest invariant und die rechte Seite nur wenn
 = \vec{F}(\vec{r},\ldots))
Aus der Galileiinvarianz und der Zeittranslationsinvarianz bekommen wir mit praktisch demselben Argument, die Unabhängigkeit von  und und  . Also . Also

Damit ist nur noch das konstante Kraftfeld übrig. Das wird man nun mit der Isotropie los, denn der einzige rotationsinvariante Vektor ist  . .
Damit ist gezeigt, daß
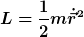
eine mögliche (r-unabhängige) Lagrangefunktion für ein freies Teilchen ist. Es ist natürlich nicht die einzige. Auch

liefert die Bewegungsgleichungen eines freien Teilchens, was nochmal zeigt, daß man die Behauptung im Skript gar nicht streng herleiten kann, selbst wenn man die komplette Galileiinvarianz der Lagrangegleichungen voraussetzt. |
|
 |
Lagrangemechaniker
Anmeldungsdatum: 04.06.2020
Beiträge: 4
|
 Lagrangemechaniker Verfasst am: 06. Jun 2020 18:05 Titel: Lagrangemechaniker Verfasst am: 06. Jun 2020 18:05 Titel: |
 |
|
Ich danke dir vielmals für deine Erklärungen, sie sind sehr verständlich.
| index_razor hat Folgendes geschrieben: | | Lagrangemechaniker hat Folgendes geschrieben: |
Ich dachte das sei einfach die Definition für "freies Teilchen".
|
Die Frage ist, was daraus für die Lagrangegleichungen folgt. Ansonsten hilft diese Definition nicht weiter.
|
Achso, ich denke ein gute und richtige Definition wäre dann, dass ein "freies Teilchen" im Inertialsystem eine gleichförmige, geradlinige Bewegung ausführt oder ruht.
| index_razor hat Folgendes geschrieben: | | Lagrangemechaniker hat Folgendes geschrieben: |
https://www.maths.tcd.ie/~frolovs/AdvMech/Notes_Lagrangian_Mechanics.pdf
Das ist kein richtiges Zitat gewesen, aber ich bin mir eigentlich sicher, dass es den Inhalt von diesem Text ab Seite 15 "1.3 Lagrangians of various systems" bis zum Ende von Seite 16 (wo es dann auch um ein einziges Teilchen geht), zusammenfasst.
|
Ja, da stimme ich dir zu. Wie mein Gegenbeispiel allerdings zeigt, ist die Behauptung auf S. 15 falsch.
|
Das komische ist halt, dass das Skript das ich hier verlinkt habe, nicht das einzige ist das so argumentiert. Das macht so mehr oder weniger jedes Skript (also zumindest die Skripte, die die Lagrange-Funktion über die Wirkung herleiten). Inklusive meinem Lehrbuch das ich zuhause hab (Lehrbuch der theoretischen Physik I. Mechanik von L.D. Landau und E.M. Lifschitz).
Bzw. um etwas genauer zu sein; ein Teil dieser Skripte sagt nur, dass L (unter den bereits besprochenen Umständen) unabhängig von r sein muss, weil der Raum homogen ist, und zwar ohne überhaupt zu sagen was ein "homogener Raum" konkret sein soll.
Der andere Teil (worunter auch das verlinkte fällt) führt die homogenität des Raumes etwas weiter aus und sagt, dass dort die Bewegungsgleichugen eines freien Teilchens (wie oben definiert) invariant unter Translation sind.
Ich mein... haben die jetzt alle irgendwie unrecht?! Bei interesse kann ich noch mehr Skripte verlinken oder mein Buch zitieren. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 07. Jun 2020 12:56 Titel: index_razor Verfasst am: 07. Jun 2020 12:56 Titel: |
 |
|
| Lagrangemechaniker hat Folgendes geschrieben: | Ich danke dir vielmals für deine Erklärungen, sie sind sehr verständlich.
|
Keine Ursache. Es freut mich, wenn es weiterhilft.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Lagrangemechaniker hat Folgendes geschrieben: |
Ich dachte das sei einfach die Definition für "freies Teilchen".
|
Die Frage ist, was daraus für die Lagrangegleichungen folgt. Ansonsten hilft diese Definition nicht weiter.
|
Achso, ich denke ein gute und richtige Definition wäre dann, dass ein "freies Teilchen" im Inertialsystem eine gleichförmige, geradlinige Bewegung ausführt oder ruht.
|
Ja, ich denke das ist eine gute Definition. Aus ihr folgt auch ohne weitere Umscheife über Symmetrieprinzipien die richtige Bewegungsgleichung 
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Lagrangemechaniker hat Folgendes geschrieben: |
https://www.maths.tcd.ie/~frolovs/AdvMech/Notes_Lagrangian_Mechanics.pdf
Das ist kein richtiges Zitat gewesen, aber ich bin mir eigentlich sicher, dass es den Inhalt von diesem Text ab Seite 15 "1.3 Lagrangians of various systems" bis zum Ende von Seite 16 (wo es dann auch um ein einziges Teilchen geht), zusammenfasst.
|
Ja, da stimme ich dir zu. Wie mein Gegenbeispiel allerdings zeigt, ist die Behauptung auf S. 15 falsch.
|
Das komische ist halt, dass das Skript das ich hier verlinkt habe, nicht das einzige ist das so argumentiert. Das macht so mehr oder weniger jedes Skript (also zumindest die Skripte, die die Lagrange-Funktion über die Wirkung herleiten). Inklusive meinem Lehrbuch das ich zuhause hab (Lehrbuch der theoretischen Physik I. Mechanik von L.D. Landau und E.M. Lifschitz).
|
Mich hat das Argument auch an Landau, Lifschitz erinnert, und ich dachte auch zuerst dies wäre deine einzige Quelle. Deswegen habe ich nochmal nachgelesen, wie ihr Argument genau geht.
Interessanterweise behandeln sie die Boostinvarianz anscheinend anders als die Translationsinvarianz.
Auf S. 6 schreiben sie: "Die Homogenität des Raumes und der Zeit bedeutet, daß diese Funktion [die Lagrangefunktion] weder den Radiusvektor 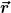 noch die Zeit noch die Zeit  explizit enthalten kann..." Also "bedeutet" offenbar Homogenität einfach die Invarianz von L und damit die Unabhängigkeit von der entsprechenden Variablen, was nach einer Definition klingt. explizit enthalten kann..." Also "bedeutet" offenbar Homogenität einfach die Invarianz von L und damit die Unabhängigkeit von der entsprechenden Variablen, was nach einer Definition klingt.
Natürlich schließen sie aus der Boostinvarianz nicht analog, daß L nicht von v abhängen darf. Stattdessen schreiben sie auf S. 8: "Da die Bewegungsgleichungen in allen Inertialsystemen dieselbe Form haben müssen, so muß die Lagrangefunktion ) bei dieser Transformation in die Funktion bei dieser Transformation in die Funktion  übergehen, die sich von übergehen, die sich von ) höchstens um die totale Ableitung einer Funktion der Koordinaten und der Zeit unterschieden kann..." höchstens um die totale Ableitung einer Funktion der Koordinaten und der Zeit unterschieden kann..."
Die Frage ist also: wenn man im Falle der Galileiboosts eine gewisse Änderung von L zulassen muß, warum nicht auch bei den Translationen? Es ist schon eigenartig, daß sie auf diesen Unterschied mit keinem Wort eingehen. Es ist schwierig zu erkennen wie man hierfür ohne implizite Annahmen über die Form von L, die man erst ableiten will, eine Rechtfertigung finden sollte bzw. wie man hinreichende Zusatzannahmen formulieren könnte, ohne daß das Argument zirkulär wird.
Ich sehe im Augenblick nur die Möglichkeit die Bewegungsgleichungen in der Form
 = 0)
anzusetzen (was recht allgemein ist) und aus der Invarianz dieser Gleichung unter der vollen Galileigruppe  zu schließen. Damit folgt zu schließen. Damit folgt
)
Der letzte Term hat keinen Einfluß auf die Lagrangegleichungen, also kann man setzen

| Zitat: |
Bzw. um etwas genauer zu sein; ein Teil dieser Skripte sagt nur, dass L (unter den bereits besprochenen Umständen) unabhängig von r sein muss, weil der Raum homogen ist, und zwar ohne überhaupt zu sagen was ein "homogener Raum" konkret sein soll.
Der andere Teil (worunter auch das verlinkte fällt) führt die homogenität des Raumes etwas weiter aus und sagt, dass dort die Bewegungsgleichugen eines freien Teilchens (wie oben definiert) invariant unter Translation sind.
Ich mein... haben die jetzt alle irgendwie unrecht?! Bei interesse kann ich noch mehr Skripte verlinken oder mein Buch zitieren. |
Was die Skripte angeht spekuliere ich mal: von Landau-Lifschitz abgeschrieben... Die Lehrbuchreihe ist zweifellos ziemlich einflußreich, und es liegt nahe sich besonders bei den etwas unklaren Punkten einfach auf ihre Autorität zu berufen.
Übrigens, Arnol'd -- eine gewissermaßen unabhängige Autorität auf dem Gebiet der klassischen Mechanik -- argumentiert in seinem Lehrbuch nicht so. Ihm reicht die Feststellung (inklusive trivialem Beweis), daß L=T-U die Newtonsche Bewegungsgleichung ergibt. Warum auch nicht? |
|
 |
Lagrangemechaniker
Anmeldungsdatum: 04.06.2020
Beiträge: 4
|
 Lagrangemechaniker Verfasst am: 09. Jun 2020 14:14 Titel: Lagrangemechaniker Verfasst am: 09. Jun 2020 14:14 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: |
Interessanterweise behandeln sie die Boostinvarianz anscheinend anders als die Translationsinvarianz.
Auf S. 6 schreiben sie: "Die Homogenität des Raumes und der Zeit bedeutet, daß diese Funktion [die Lagrangefunktion] weder den Radiusvektor 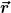 noch die Zeit noch die Zeit  explizit enthalten kann..." Also "bedeutet" offenbar Homogenität einfach die Invarianz von L und damit die Unabhängigkeit von der entsprechenden Variablen, was nach einer Definition klingt. explizit enthalten kann..." Also "bedeutet" offenbar Homogenität einfach die Invarianz von L und damit die Unabhängigkeit von der entsprechenden Variablen, was nach einer Definition klingt.
Natürlich schließen sie aus der Boostinvarianz nicht analog, daß L nicht von v abhängen darf. Stattdessen schreiben sie auf S. 8: "Da die Bewegungsgleichungen in allen Inertialsystemen dieselbe Form haben müssen, so muß die Lagrangefunktion ) bei dieser Transformation in die Funktion bei dieser Transformation in die Funktion  übergehen, die sich von übergehen, die sich von ) höchstens um die totale Ableitung einer Funktion der Koordinaten und der Zeit unterschieden kann..." höchstens um die totale Ableitung einer Funktion der Koordinaten und der Zeit unterschieden kann..."
Die Frage ist also: wenn man im Falle der Galileiboosts eine gewisse Änderung von L zulassen muß, warum nicht auch bei den Translationen? Es ist schon eigenartig, daß sie auf diesen Unterschied mit keinem Wort eingehen. Es ist schwierig zu erkennen wie man hierfür ohne implizite Annahmen über die Form von L, die man erst ableiten will, eine Rechtfertigung finden sollte bzw. wie man hinreichende Zusatzannahmen formulieren könnte, ohne daß das Argument zirkulär wird.
Ich sehe im Augenblick nur die Möglichkeit die Bewegungsgleichungen in der Form
 = 0)
anzusetzen (was recht allgemein ist) und aus der Invarianz dieser Gleichung unter der vollen Galileigruppe  zu schließen. Damit folgt zu schließen. Damit folgt
)
Der letzte Term hat keinen Einfluß auf die Lagrangegleichungen, also kann man setzen

|
Abgeshen davon, dass die Argumentaion von Landau, Lifschitz etwas seltsam ist, wirkt sie zusätzlich noch unnötig kompliziert, was es für mich noch komischer macht, dass sie diesen Weg gegangen sind.
Ich hab mir den Anfang vom Buch nochmal durchgelesen und auch eine Idee bekommen, wie man die Argumentation von Landau, Lifschitz evtl. interpretieren kann:
Dazu erstmal 2 Zitate
"Nach diesem Prinzip [Prinzip der kleinsten Wirkung] ist jedes mechanische System durch eine bestimmte Funktion charakterisiert: ) " ( S.2) " ( S.2)
"In einem beliebigen Bezugssystem ist der Raum im allgemeinen weder homogen noch isotrop. Das bedeutet, dass verschiedene Lagen im Raum und verschiedene Richtungen in mechanischer Hinsicht nicht äquivalent sind, selbst wenn der betrachtete Körper in keiner Wechselwirkung mit anderen Körpern steht." (S.5-6)
Vielleicht wollen sie L nicht nur so konstruieren, dass es ein mechanisches System beschreiben kann, sondern dass L eine Art "Äquivalent" zum mechansichen System ist. Damit mein ich, dass L alle Eigenschaften eines mechanischen Systems in sich vereinen soll.
Konkret im Fall des freien Teilchens; da es nicht mit seiner Umwelt wechselwirkt, ist es egal wo es sich befindet und von wo aus es betrachtet wird (homogenität des Raumes), deshalb sollte auch L unabhängig von r sein.
Wenn man bei einem freien Teilchen eine Boost-transformation macht, also die Geschwindigkeit um eine konstante erhöht, dann ändert man das mechanische System, also soll sich auch L ändern.
Was hältst du davon, plausible Interpretation?
Mir ist beim lesen dann auch nochmal was aufgefallen, was ich nicht verstehe:
| index_razor hat Folgendes geschrieben: |
"Da die Bewegungsgleichungen in allen Inertialsystemen dieselbe Form haben müssen, so muß die Lagrangefunktion ) bei dieser Transformation in die Funktion bei dieser Transformation in die Funktion  übergehen, die sich von übergehen, die sich von ) höchstens um die totale Ableitung einer Funktion der Koordinaten und der Zeit unterschieden kann..." höchstens um die totale Ableitung einer Funktion der Koordinaten und der Zeit unterschieden kann..."
|
Mir ist zwar klar, dass die Lagrange-Gleichungen invariant unter L + einer Funktion ) sind, mir ist aber noch nicht ganz klar, dass das die einzige Möglichkeit sein soll. Auf S.5 besprechen sie diesen Sachverhalt, mir wird dort allerdings nur deutlich, dass das eine Möglichekit ist. sind, mir ist aber noch nicht ganz klar, dass das die einzige Möglichkeit sein soll. Auf S.5 besprechen sie diesen Sachverhalt, mir wird dort allerdings nur deutlich, dass das eine Möglichekit ist.
Falls es kein zu großer Aufwand ist, würde ich mich sehr freuen wenn du mir das auch noch erklären könntest.
| index_razor hat Folgendes geschrieben: |
Was die Skripte angeht spekuliere ich mal: von Landau-Lifschitz abgeschrieben... Die Lehrbuchreihe ist zweifellos ziemlich einflußreich, und es liegt nahe sich besonders bei den etwas unklaren Punkten einfach auf ihre Autorität zu berufen.
|
Wenn das wahr ist, wäre das schon irgendwie traurig, ich denke es sollte ja gerade die Arbeit eines Professoren/Dozenten sein, die unklaren Punkte etwas aufzuarbeiten und verständlicher zu machen. Ob ich mir nun meinen Kopf an einem unverständlichem Skript vom Prof zerbrech oder an einem unverständlichem Lehrbuch macht dann auch keinen Unterschied mehr.
| index_razor hat Folgendes geschrieben: |
Übrigens, Arnol'd -- eine gewissermaßen unabhängige Autorität auf dem Gebiet der klassischen Mechanik -- argumentiert in seinem Lehrbuch nicht so. Ihm reicht die Feststellung (inklusive trivialem Beweis), daß L=T-U die Newtonsche Bewegungsgleichung ergibt. Warum auch nicht?
|
Interessant wie unterschiedlich das betrachtet wird, würde mich auch mal interssieren wie das Lagrange selbst sah, im Internet hab ich dazu leider nichts gefunden. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 09. Jun 2020 15:55 Titel: index_razor Verfasst am: 09. Jun 2020 15:55 Titel: |
 |
|
| Lagrangemechaniker hat Folgendes geschrieben: |
Vielleicht wollen sie L nicht nur so konstruieren, dass es ein mechanisches System beschreiben kann, sondern dass L eine Art "Äquivalent" zum mechansichen System ist. Damit mein ich, dass L alle Eigenschaften eines mechanischen Systems in sich vereinen soll.
Konkret im Fall des freien Teilchens; da es nicht mit seiner Umwelt wechselwirkt, ist es egal wo es sich befindet und von wo aus es betrachtet wird (homogenität des Raumes), deshalb sollte auch L unabhängig von r sein.
Wenn man bei einem freien Teilchen eine Boost-transformation macht, also die Geschwindigkeit um eine konstante erhöht, dann ändert man das mechanische System, also soll sich auch L ändern.
|
Wieso ändert ein Boost das System? Das ist doch lediglich eine Symmetrietransformation und als solche prinzipiell nicht anders als eine Translation.
| Zitat: |
Was hältst du davon, plausible Interpretation?
|
Ich denke sie wollen ein möglichst einfaches L konstruieren. Dazu übernehmen sie möglichst viele Symmetrien aus den Bewegungsgleichungen in L, müssen aber vermeiden, daß L dadurch trivial wird.
Also L unabhängig von r und t zu wählen, ist möglich und führt zu translationsinvarianten Bewegungsgleichungen. Trotz Galileiinvarianz dieser Gleichungen ist es aber nicht möglich, L unabhängig von v zu wählen, weil sonst L=const. und jede Kurve die Lagrangegleichungen erfüllt. Also ist L eine Funktion allein von v. Wegen der Rotationsinvarianz lediglich eine von 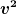 und wegen der Boostinvarianz ist sie linear in und wegen der Boostinvarianz ist sie linear in 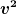 . .
Ich denke das ist im wesentlichen ihr Argument.
| Zitat: |
Mir ist beim lesen dann auch nochmal was aufgefallen, was ich nicht verstehe:
| index_razor hat Folgendes geschrieben: |
"Da die Bewegungsgleichungen in allen Inertialsystemen dieselbe Form haben müssen, so muß die Lagrangefunktion ) bei dieser Transformation in die Funktion bei dieser Transformation in die Funktion  übergehen, die sich von übergehen, die sich von ) höchstens um die totale Ableitung einer Funktion der Koordinaten und der Zeit unterschieden kann..." höchstens um die totale Ableitung einer Funktion der Koordinaten und der Zeit unterschieden kann..."
|
Mir ist zwar klar, dass die Lagrange-Gleichungen invariant unter L + einer Funktion ) sind, mir ist aber noch nicht ganz klar, dass das die einzige Möglichkeit sein soll. Auf S.5 besprechen sie diesen Sachverhalt, mir wird dort allerdings nur deutlich, dass das eine Möglichekit ist. sind, mir ist aber noch nicht ganz klar, dass das die einzige Möglichkeit sein soll. Auf S.5 besprechen sie diesen Sachverhalt, mir wird dort allerdings nur deutlich, dass das eine Möglichekit ist.
Falls es kein zu großer Aufwand ist, würde ich mich sehr freuen wenn du mir das auch noch erklären könntest.
|
Dazu muß man nur zeigen, daß jede triviale Lagrangefunktion, also eine, deren Lagrangegleichungen von jeder Funktion erfüllt werden, eine totale Zeitableitung ist. (Denn zwei Lagrangefunktionen, die dieselben Lagrangegleichungen ergeben, unterscheiden sich nur um eine solche triviale Funktion.) Sei also ) trivial. Dann ist trivial. Dann ist
 = \left(\frac{\partial L}{\partial\vec{r}} - \frac{\dd}{\dd t}\frac{\partial L}{\partial\dot{\vec{r}}}\right)\cdot\vec{r} + \frac{\dd}{\dd t}\left(\vec{r}\cdot\frac{\partial}{\partial{\dot{\vec{r}}}} L(\epsilon\vec{r}, \epsilon\dot{\vec{r}}, t)\right))
Da L trivial ist, verschwindet der erste Term auf der rechten Seite. Jetzt integriert man über  von 0 bis 1 von 0 bis 1
 = L(0, 0, t) + \frac{\dd}{\dd t}\left(\ldots\right))
und wählt irgendeine Stammfunktion von ) , sagen wir , sagen wir ) . Dann gilt . Dann gilt
 = \frac{\dd}{\dd t}\left(\int_0^1 \vec{r}\cdot\frac{\partial}{\partial{\dot{\vec{r}}}} L(\epsilon\vec{r}, \epsilon\dot{\vec{r}}, t)\ \dd\epsilon + \Lambda(t)\right).)
Dieses Argument ist im wesentlichen eine vereinfachte Version des Beweises von Theorem 4.7 aus Olver, Applications of Lie Groups to Differential Equations. |
|
 |
Lagrangemechaniker
Anmeldungsdatum: 04.06.2020
Beiträge: 4
|
 Lagrangemechaniker Verfasst am: 10. Jun 2020 14:35 Titel: Lagrangemechaniker Verfasst am: 10. Jun 2020 14:35 Titel: |
 |
|
Vielen Dank für den Beweis, deine Hilfe ist für mich wirklich Gold wert!
| index_razor hat Folgendes geschrieben: | | Lagrangemechaniker hat Folgendes geschrieben: |
Vielleicht wollen sie L nicht nur so konstruieren, dass es ein mechanisches System beschreiben kann, sondern dass L eine Art "Äquivalent" zum mechansichen System ist. Damit mein ich, dass L alle Eigenschaften eines mechanischen Systems in sich vereinen soll.
Konkret im Fall des freien Teilchens; da es nicht mit seiner Umwelt wechselwirkt, ist es egal wo es sich befindet und von wo aus es betrachtet wird (homogenität des Raumes), deshalb sollte auch L unabhängig von r sein.
Wenn man bei einem freien Teilchen eine Boost-transformation macht, also die Geschwindigkeit um eine konstante erhöht, dann ändert man das mechanische System, also soll sich auch L ändern.
|
Wieso ändert ein Boost das System? Das ist doch lediglich eine Symmetrietransformation und als solche prinzipiell nicht anders als eine Translation.
|
Bei einer Translation ändert sich zwar der Ort, wenn man aber sagt, dass es keine ausgezeichneten Raumpunkte gibt, ist das eine triviale Änderung.
Bei einem Boost ändert man die Energie des Systems, was evtl. keine triviale Änderung ist? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 10. Jun 2020 15:06 Titel: index_razor Verfasst am: 10. Jun 2020 15:06 Titel: |
 |
|
| Lagrangemechaniker hat Folgendes geschrieben: | | Zitat: |
Wieso ändert ein Boost das System? Das ist doch lediglich eine Symmetrietransformation und als solche prinzipiell nicht anders als eine Translation.
|
Bei einer Translation ändert sich zwar der Ort, wenn man aber sagt, dass es keine ausgezeichneten Raumpunkte gibt, ist das eine triviale Änderung.
Bei einem Boost ändert man die Energie des Systems, was evtl. keine triviale Änderung ist? |
Hm, wenn man sagt, daß es keine ausgezeichneten Inertialsysteme gibt, impliziert das dann nicht ebenso, daß alle Änderungen, die vom Wechsel des Inertialsystems abhängen, eben doch trivial sind? Das schließt natürlich die kinetische Energie mit ein. Ich glaube ich verstehe schon so ungefähr, worauf du hinauswillst, aber für mich bleibt das ein zirkuläres Argument. |
|
 |
|
|















