| Autor |
Nachricht |
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 296
|
 Corbi Verfasst am: 06. Mai 2020 13:25 Titel: Feynman-Regeln aus Lagrangefunktion finden |
 |
|
Hi,
ich bin noch ein blutiger Anfänger in der QFT und habe bisher noch nicht viele Zusammenhänge verstanden deshalb müsst ihr vielleicht etwas Geduld haben.
Es geht um 3 Elementarteilchen:
 : massives Spin-1-Teilchen mit Masse 
2 Dirac-Fermionen q und Q mit Masse m und M.
Die Interaktion dieser Teilchen wird durch folgende Lagrangefunktion beschrieben:
Q + adj.])
Dabei ist 
 sind komplexe konstanten.
"adj." steht für den selben Term in adjungiert.
Meine Aufgabe ist es die Feynman-Regeln für alle möglichen Vertices zu finden. Ich habe bisher absolut keine Idee wie ich da vorgehen soll und bin aus den Vorlesungsnotizen und dem einzigen Buch (Peskin/Schroeder) das ich zur Hand habe nicht wirklich schlau geworden.
Bin über jede Hilfe dankbar!
(bei mir werden die Formeln grade nicht richtig angezeigt, ich hoffe ich habe alles richtig eingegeben)
Zuletzt bearbeitet von Corbi am 07. Mai 2020 11:36, insgesamt einmal bearbeitet |
|
 |
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
| jh8979 Verfasst am: 06. Mai 2020 16:22 Titel: |
|
|
|
Im Kapitel 4 beschreibt P&S es doch ganz gut, insbesondere Kapitel 4.4. |
|
|
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 296
|
| Corbi Verfasst am: 06. Mai 2020 17:30 Titel: |
|
|
Ich kapier hald garnicht wie ich das jetzt auf 3 unterschiedliche Felder mit den gegebenen Eigenschaften anwende.
Was wäre denn jetzt der analoge Ausdruck zu Gleichung (4.31) (P&S) bei meinem Problem ?
P.S ist das Problem mit den Formeln ein Problem von Physikerboard oder von meinem PC&Handy ? |
|
|
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 296
|
| Corbi Verfasst am: 06. Mai 2020 17:57 Titel: |
|
|
Da die Aufgabe so formuliert ist "write down the Feynman-Rules for all vertices" und es die erste Teilaufgabe von einer recht langen Aufgabe ist, gehe ich auch mal davon aus, dass man sie nicht unbedingt von Grundauf ableiten soll sondern vielleicht in Analogie zur QED einfach erraten kann.
Aber wie gesagt ich hab die Grundstruktur der Theorie noch nicht wirklich durchschaut. Für mich ist das bisher einfach ein riesiges Gewirr aus Formeln |
|
|
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 296
|
| Corbi Verfasst am: 06. Mai 2020 18:19 Titel: |
|
|
könnte für eine Vertex 
nicht irgendwie sowas rauskommen:
 \gamma^{\mu} ) |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
| jh8979 Verfasst am: 06. Mai 2020 20:16 Titel: |
|
|
| Corbi hat Folgendes geschrieben: | könnte für eine Vertex
nicht irgendwie sowas rauskommen:
V_{\mu} \rightarrow \bar{q}Q = -iq(g_R + g_L) \gamma^{\mu} |
Das q rechts ist zuviel, es fehlen die Projektionsmatrzen P_L/R und gamma^mu steht dann auf der falschen Seite der P_L/R. |
|
|
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 296
|
| Corbi Verfasst am: 06. Mai 2020 22:14 Titel: |
|
|
ok also:
V_{\mu} \rightarrow \bar{q}Q = -i\gamma^{\mu}(g_R P_R + g_L P_L)
?
Das q ist zuviel weil die Kopplung durch eine "Ladung" bereits durch g_r und g_l geleistet wird ? |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
| jh8979 Verfasst am: 07. Mai 2020 07:36 Titel: |
|
|
Ja.
PS: Ich würde den Vertex aber nicht nennen, da er auch andere Übergänge beschreibt. |
|
|
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 296
|
| Corbi Verfasst am: 07. Mai 2020 11:34 Titel: |
|
|
Allright.
Was muss ich für das massive  -Teilchen beachten, im vergleich zum Photon in der QED ?
Kann ich da dieselben Formeln wie in der QED verwenden ? |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
|
|
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 296
|
| Corbi Verfasst am: 09. Mai 2020 16:14 Titel: |
|
|
Ich soll jetzt das Matrix-element für einen Prozess:
 berechnen.
Ich bin etwas verwirrt. Die vollständige Lagrangefunktion lautet:
Q + \bar{Q} \gamma^{\mu} (g_L^* P_L + g_R^* P_R)q] )
Es gibt also keine Vertex für den oben genannten Prozess und ich komm nicht drauf wie ich den Prozess aus erlaubten Diagrammen zusammensetzen soll.
Ist das überhaupt möglich ? |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
| jh8979 Verfasst am: 09. Mai 2020 16:23 Titel: |
|
|
Ja, natürlich. Das ist der ja genau der Wechselwirkungsterm.
(Du siehst hier schön, wieso ich Deine Bezeichnung oben nicht gut fand.)
Vorgehen wie in der QED:
1. Feynman-Diagramm zeichnen.
2. Fermionlinien entgegen der Pfeilrichtung abgehen und entsprechenden Regeln anwenden (bar-u für ausgehendes Teilchen, v für eingehendes Antiteilchen, ...., Vertizes/Propagatoren einfügen,...)
3. Rest des Diagramms abarbeiten.
4. Jetzt hat man i*M (oder -i*M, vergess ich immer, ist aber egal): Also mit dem Komplezkonjugierten multiplizieren (Vorsicht mit der Reihenfolge der Gammas etc).
5. Evtl Summen über Spinmittelungen ausführen, Spurformeln benutzen, etc
..
usw.
Ich finde das ist im Peskin sehr gut erklärt: WIE man damit rechnet. Schau Dir mal Kapitel 5 an. Da ist ein einfaches Beispiel. (Deine Aufgabe ist in der Tat noch ein kleines bisschen leichter) |
|
|
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 296
|
| Corbi Verfasst am: 09. Mai 2020 16:50 Titel: |
|
|
Wie die Rechnung funktioniert ist mir einigermaßen klar.
Ich dachte gerade nur dass es keine Vertices gibt, die ein q-Fermion mit einem Q-Fermion verbinden.
Aber es ist ja im Prinzip wie ein Elektron, das ein Photon emittiert. Nur dass in diesem Fall kein neues Q-Fermion sondern ein q-Fermion herauskommt. |
|
|
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 296
|
| Corbi Verfasst am: 09. Mai 2020 17:12 Titel: |
|
|
|
wenn ich über die Spins Summiere muss ich dann auch über die Photon-polarisationen summieren ? |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
| jh8979 Verfasst am: 09. Mai 2020 17:37 Titel: |
|
|
| Corbi hat Folgendes geschrieben: | Wie die Rechnung funktioniert ist mir einigermaßen klar.
Ich dachte gerade nur dass es keine Vertices gibt, die ein q-Fermion mit einem Q-Fermion verbinden.
Aber es ist ja im Prinzip wie ein Elektron, das ein Photon emittiert. Nur dass in diesem Fall kein neues Q-Fermion sondern ein q-Fermion herauskommt. |
Genau. |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
| jh8979 Verfasst am: 09. Mai 2020 17:40 Titel: |
|
|
| Corbi hat Folgendes geschrieben: | | wenn ich über die Spins Summiere muss ich dann auch über die Photon-polarisationen summieren ? |
Ob Du über ein/ausgehende Spins summieren musst, hängt davon ab was Du berechnen willst. Wenn der Eingangsspin feststeht, und ausgehender Spin und Polarisation gemessen werden, dann wird gar nichts summiert.
Wenn in der Aufgabe nicht mehr gegeben ist, würde ich aber denken, dass über eingehende Spins/Polarisationen gemittelt wird und ausgehende summiert werden. |
|
|
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 296
|
| Corbi Verfasst am: 22. Mai 2020 19:50 Titel: |
|
|
Ok, z.B. bei der Compton-Streuung verwendet man dann foglenden Ausdruck:
Der Faktor 1/4 kommt dabei vom Mitteln der eingehenden Spins, was einen Faktor 1/2 bedeutet und durch das Betragsquadrat erhält man dann 1/4 ? |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 23. Mai 2020 17:21 Titel: |
|
|
| Corbi hat Folgendes geschrieben: | Ok, z.B. bei der Compton-Streuung verwendet man dann foglenden Ausdruck:
Der Faktor 1/4 kommt dabei vom Mitteln der eingehenden Spins, was einen Faktor 1/2 bedeutet und durch das Betragsquadrat erhält man dann 1/4 ? |
Bei der Compton-Streuung mußt du zwei Spinvariablen berücksichtigen; den des Elektrons 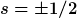 und die Polarisation des Photons,  . Da für beide je zwei Möglichkeiten bestehen, ist die Spinkonfiguration des in-Zustands ein Produkt aus zwei 2x2-Matrizen,
(Hier geht bereits die Annahme ein, daß die Polarisationszustände der beiden einlaufenden Teilchen unkorreliert sind und daß außerdem keine Interferenz zwischen den möglichen Spinzuständen besteht. Das läßt sich natürlich verallgemeinern.) Für den out-Zustand gilt also
S^\dagger = \sum_{s,\epsilon}p_s p_\epsilon S|s,\epsilon\rangle\langle s,\epsilon|S^\dagger)
Ich ignoriere die Variable für den Impulsübertrag, von der S natürlich auch abhängt. Für den Fall, daß beide in-Zustände vollkommen unpolarisiert sind, gilt also
und damit
Im letzten Schritt wird berücksichtigt, daß ) man sich aber ja normalerweise nur für den Fall interessiert, daß irgendein Impulsübertrag stattgefunden hat. Zumindest ist dies die Voraussetzung, die der Definition des Wirkungsquerschnitts zugrunde liegt.
Der Faktor 1/4 kommt also nicht vom Betragsquadrat, sondern aus den Faktoren der initialen Dichtematrizen.
Das Produkt auf der rechten Seite beschreibt nun die komplette Information über die Spinkonfiguration der finalen Zustände. Man könnte hieraus insbesondere die Wahrscheinlichkeiten und den Wirkungsquerschnitt für einen bestimmte finale Spinkonfiguration ausrechnen
=\text{Tr}(P_{s\epsilon}\rho_\text{out}) \propto \text{Tr}(P_{s\epsilon}MM^\dagger).)
Wenn die Spins gar nicht gemessen werden, steht anstelle des Projektors  einfach der Einheitsoperator (Projektor auf den gesamten Hilbertraum der möglichen Spinkonfigurationen) und deswegen ist
 \propto \text{Tr}(MM^\dagger)\propto \frac{\dd \sigma}{\dd \Omega}(\vec{p}_\text{in}\to\vec{p}_\text{out}) .)
Die Spur ist genau die Spinsumme über die Spins des Endzustandes, also vermutlich das, was bei dir als  ausgedrückt ist. |
|
|
|
Registrieren
Login
FAQ
Suchen
