| Autor |
Nachricht |
Physikhilfeamsonntag
Anmeldungsdatum: 29.03.2020
Beiträge: 1
|
 Physikhilfeamsonntag Verfasst am: 29. März 2020 19:41 Titel: Messunsicherheit Physikhilfeamsonntag Verfasst am: 29. März 2020 19:41 Titel: Messunsicherheit |
 |
|
Meine Frage:
Guten Tag,
Ich habe den Mittelwert verschiedener Messungen (8 Messungen) von der Wellenlänge eines Lasers.
Der Mittelwert ist: 629,909375nm
Ich will laut Aufgabe den Mittelwert mit Unsicherheit bestimmen.
Als Tipp war dort, die Standardabweichung auszurechnen.
Meine Ideen:
1 Frage: Ist die Unsicherheit genau das selbe wie die Standardabweichung?
2 Frage: Welche Formel der Standardabweichung nehme ich?
Es gibt im Skript einmal die Formel welche unter der Wurzel die Summe aller (Lambda + Mittelwert)^2 durch (n-1) teilt und es gibt einmal die Formel die sehr ähnlich aussieht, jedoch steht unter dem Bruch n*(n-1). Kann mir hier bitte jemand weiterhelfen?
Am Ende will ich mit der Unsicherheit + dem Mittelwert überprüfen, ob ich damit den Literaturwert von 632,8nm erreiche. Meine Idee war es, die Standardabweichung auszurechnen (nur welche der beiden Formeln? Bei der einen kommt ca 2nm raus, bei der anderen nur 0,7nm) und diese Zahl ist meine Messunsicherheit, die ich auf meinen Mittelwert addieren würde und mit dem Literaturwert vergleichen.
Hilfe bitte  |
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2019
|
 Nils Hoppenstedt Verfasst am: 30. März 2020 11:42 Titel: Re: Messunsicherheit Nils Hoppenstedt Verfasst am: 30. März 2020 11:42 Titel: Re: Messunsicherheit |
 |
|
| Physikhilfeamsonntag hat Folgendes geschrieben: |
1 Frage: Ist die Unsicherheit genau das selbe wie die Standardabweichung?
|
Nein, die Messunsicherheit umfasst zwei grundsätzliche Typen:
1. Die systematische Messunsichheit, die das Messergebnis in eine Richtung verschiebt (z.B. durch Offset in der Kalibrierung, schief abgelesene Skala, etc).
2. Die statistische Messunsicherheit, die mehr oder wenig symmetrisch um einen Mittelwert streut.
Der 2. Typ lässt sich mit Hilfe der Standardabweichung quantifizieren.
| Physikhilfeamsonntag hat Folgendes geschrieben: |
2 Frage: Welche Formel der Standardabweichung nehme ich?
Es gibt im Skript einmal die Formel welche unter der Wurzel die Summe aller (Lambda + Mittelwert)^2 durch (n-1) teilt und es gibt einmal die Formel die sehr ähnlich aussieht, jedoch steht unter dem Bruch n*(n-1). Kann mir hier bitte jemand weiterhelfen?
|
Die erste Formel beschreibt die statistische Messunsicherheit für eine Einzelmessung, die zweite Formel beschreibt die statistische Messunsicherheit für den Mittelwert einer Stichprobe. Da euch ja die Unsicherheit des Mittelwerts interessiert, müsst ihr also die letztere verwenden. In der Messtechnik hat sich etabliert hier den 3-fachen Wert zu nehmen. Das Ergebnis wäre also:
lambda = (629.9 +/- 2.1) nm
Ihr habt also den Literaturwert leicht verfehlt, was auf eine zusätzliche systematischen Messunsicherheit hindeutet.
Viele Grüße,
Nils |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 30. März 2020 12:46 Titel: Re: Messunsicherheit index_razor Verfasst am: 30. März 2020 12:46 Titel: Re: Messunsicherheit |
 |
|
| Physikhilfeamsonntag hat Folgendes geschrieben: |
Es gibt im Skript einmal die Formel welche unter der Wurzel die Summe aller (Lambda + Mittelwert)^2 durch (n-1) teilt und es gibt einmal die Formel die sehr ähnlich aussieht, jedoch steht unter dem Bruch n*(n-1). Kann mir hier bitte jemand weiterhelfen?
|
Als Ergänzung nochmal, was es mit den beiden Standardabweichungen auf sich hat. Jede Einzelmessung schwankt zufällig mit unbekannter Standardabweichung 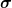 um den wahren Wert um den wahren Wert 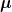 . Da das . Da das 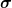 eben unbekannt ist, man weiß also nicht, wie genau die einzelne Messung ist. eben unbekannt ist, man weiß also nicht, wie genau die einzelne Messung ist.
Man weiß aber, daß, wenn immer unter denselben Bedingungen gemessen wird, der Mittelwert der Einzelergebnisse einer Meßreihe eine geringere Schwankung hat, als jeder Einzelwert, nämlich (unter recht allgemeinen Voraussetzungen)  . .
Das ist der einzige Grund, warum man überhaupt mehrmals mißt und die Ergebnisse mittelt. Man will die Unsicherheit des Ergebnisses verringern.
Eine empirische Schätzung der Standardabweichung 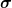 der Einzelmessung ist der Einzelmessung ist
^2}.)
Eine Schätzung für die Standardabweichung des Mittelwertes folglich
 . .
Die statistische "Meßunsicherheit" ist nun hingegen eine Schätzung der Breite der Verteilung von 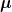 bei gegebenem bei gegebenem /n) und und  . Diese wird oft, aber nicht immer, in Form eines symmetrischen Intervalls um . Diese wird oft, aber nicht immer, in Form eines symmetrischen Intervalls um  angegeben. Man möchte mit der Wahl der Intervallgröße erreichen, daß dieses den wahren Wert mit großer Sicherheit einschließt. Normalerweise strebt man dabei Wahrscheinlichkeiten von 95% oder mehr an. Diese Wahrscheinlichkeit nennt man das Konfidenzniveau. Welches Konfidenzniveau man wählt ist, wie gesagt, keine rein statistische Frage. Unter Umständen benötigt man deutlich mehr als 99 %, manchmal reichen um die 70 %. angegeben. Man möchte mit der Wahl der Intervallgröße erreichen, daß dieses den wahren Wert mit großer Sicherheit einschließt. Normalerweise strebt man dabei Wahrscheinlichkeiten von 95% oder mehr an. Diese Wahrscheinlichkeit nennt man das Konfidenzniveau. Welches Konfidenzniveau man wählt ist, wie gesagt, keine rein statistische Frage. Unter Umständen benötigt man deutlich mehr als 99 %, manchmal reichen um die 70 %.
Im allgemeinen ist diese Meßunsicherheit, also die Schwankung von 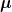 , eine Funktion von , eine Funktion von  . Ob man eine angestrebte Konfidenz durch Multiplikation mit 3 oder 1 oder irgendeiner anderen Zahl erreicht, hängt nur davon ab, wie . Ob man eine angestrebte Konfidenz durch Multiplikation mit 3 oder 1 oder irgendeiner anderen Zahl erreicht, hängt nur davon ab, wie 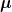 verteilt ist, was u.a. von der Verteilung der Einzelmeßwerte und der Anzahl der Messungen beeinflußt sein kann. verteilt ist, was u.a. von der Verteilung der Einzelmeßwerte und der Anzahl der Messungen beeinflußt sein kann.
Wenn man z.B. aus irgendwelchen Gründen wüßte, daß 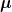 gaußverteilt ist, dann läge das Konfidenzniveau von 95 % bei ca 1.96 Standardabweichung. Wenn man dies anstrebt, würde es in diesem Fall also reichen gaußverteilt ist, dann läge das Konfidenzniveau von 95 % bei ca 1.96 Standardabweichung. Wenn man dies anstrebt, würde es in diesem Fall also reichen  mit 1.96 zu multiplizieren. (Woher man allerdings die nötige Information über mit 1.96 zu multiplizieren. (Woher man allerdings die nötige Information über 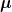 haben sollte, ist eine andere Frage.) haben sollte, ist eine andere Frage.)
In eurem Fall liegt mit ziemlicher Sicherheit keine Gaußverteilung vor, sondern wie gesagt vermutlich eine t-Verteilung. Dafür ist bei einem Umfang von 8 Messung der Faktor 3 schon angemessen (ca. 97 %). Faktor 2 wäre jedenfalls ein paar Prozent unsicherer. Wenn man deutlich sicherer sein will als 99.9 % kann es sein, daß Faktor 3 nicht reicht. |
|
 |
|
|
















