| Autor |
Nachricht |
Lehramtsstudent
Anmeldungsdatum: 11.03.2018
Beiträge: 77
|
 Lehramtsstudent Verfasst am: 22. Feb 2020 16:45 Titel: Warum ist das Huygensprinzip (auch makroskopisch) falsch? Lehramtsstudent Verfasst am: 22. Feb 2020 16:45 Titel: Warum ist das Huygensprinzip (auch makroskopisch) falsch? |
 |
|
In diesem Video wird bei 7:52 gesagt, dass das Huygensprinzip falsch sei: https://www.youtube.com/watch?v=NLmpNM0sgYk
Begründet wird es damit, dass die Lichtausbreitung bei der Brechung im Glas auch in anderen Richtungen als der nach Snellius vorgegebenen Richtung vorhanden sei. Ist das ein triftiger Einwand? Ich habe den noch nie vorher gehört. Hier geht es ja auch noch nicht um Beugung, sondern ganz makroskopisch...
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 22. Feb 2020 18:16 Titel: Nils Hoppenstedt Verfasst am: 22. Feb 2020 18:16 Titel: |
 |
|
|
Hier wird leider das Huygensche Prinzip nicht richtig angewendet. Es besagt nämlich, dass man die neue Wellenfront erhält, indem man die äußere Einhüllende aller Elementarwellen bildet. Die in dem Video gezeigten alternativen Wellenfronten verbinden zwar die Wellenberge benachbarter Elementarwellen, aber sie bilden zu keinem Zeitpunkt die äußere Einhüllende des Wellenfeldes.
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 22. Feb 2020 18:19 Titel: Re: Warum ist das Huygensprinzip (auch makroskopisch) falsch index_razor Verfasst am: 22. Feb 2020 18:19 Titel: Re: Warum ist das Huygensprinzip (auch makroskopisch) falsch |
 |
|
Dort wird nicht behauptet das Huygensche Prinzip sei falsch, sondern lediglich, daß es keine Erklärung für das Brechungsgesetz liefert.
| Zitat: |
Begründet wird es damit, dass die Lichtausbreitung bei der Brechung im Glas auch in anderen Richtungen als der nach Snellius vorgegebenen Richtung vorhanden sei.
|
Das Huygensche Prinzip besagt ja nur, daß die gesamte Welle wieder die Summe einzelner Elementarwellen ist, die von der Wellenfront ausgehen. Das besagt überhaupt nichts darüber, wo die Wellenfront verläuft und wie der Verlauf sich beim Übergang zu einem anderen Medium ändert. Das ist aber gerade was das Brechungsgesetz angeben soll.
Insofern denke ich, daß Dr. Don Lincoln vollkommen recht hat und auch nichts wirklich kontroverses behauptet.
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 22. Feb 2020 19:18 Titel: index_razor Verfasst am: 22. Feb 2020 19:18 Titel: |
 |
|
| Nils Hoppenstedt hat Folgendes geschrieben: | | Hier wird leider das Huygensche Prinzip nicht richtig angewendet. Es besagt nämlich, dass man die neue Wellenfront erhält, indem man die äußere Einhüllende aller Elementarwellen bildet. Die in dem Video gezeigten alternativen Wellenfronten verbinden zwar die Wellenberge benachbarter Elementarwellen, aber sie bilden zu keinem Zeitpunkt die äußere Einhüllende des Wellenfeldes. |
Ich denke du hast die Behauptung im Video falsch verstanden. Der Punkt ist doch gerade, daß du nicht weißt, wie genau diese Summe "aller" Elementarwellen aussieht, ohne jegliche Kentniss des Verlaufs der Wellenfront zu haben. Im Video wird ab Minute 7:55 behauptet, daß nun "alle" Elementarwellen in Betracht gezogen werden. Die Einhüllende der Summe liegt aber eben nicht senkrecht zur Ausbreitungsrichtung (8:23). Woher soll man nun wissen, daß dies nicht korrekt ist?
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 22. Feb 2020 19:30 Titel: Nils Hoppenstedt Verfasst am: 22. Feb 2020 19:30 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: |
Ich denke du hast die Behauptung im Video falsch verstanden.
|
Na, ich denke doch schon. Es wird behauptet, dass man mit dem Huygenschen Prinzip die Ausbreitungsrichtung nicht eindeutig bestimmen kann. Das ist aber nicht richtig.
| index_razor hat Folgendes geschrieben: | | Der Punkt ist doch gerade, daß du nicht weißt, wie genau diese Summe "aller" Elementarwellen aussieht, ohne jegliche Kentniss des Verlaufs der Wellenfront zu haben. Im Video wird ab Minute 7:55 behauptet, daß nun "alle" Elementarwellen in Betracht gezogen werden. Die Einhüllende der Summe liegt aber eben nicht senkrecht zur Ausbreitungsrichtung. Woher soll man nun wissen, daß dies nicht korrekt ist? |
Wie gesagt: es geht um die äußere Einhüllende zu einem beliebigen Zeitpunkt (wie es im Video auch vorher gezeigt). Damit wird es dann auch eindeutig.
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 22. Feb 2020 19:42 Titel: index_razor Verfasst am: 22. Feb 2020 19:42 Titel: |
 |
|
| Nils Hoppenstedt hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: |
Ich denke du hast die Behauptung im Video falsch verstanden.
|
Na, ich denke doch schon. Es wird behauptet, dass man mit dem Huygenschen Prinzip die Ausbreitungsrichtung nicht eindeutig bestimmen kann. Das ist aber nicht richtig.
|
Wieso nicht? Wie bestimmst du denn mit den Huygenschen Prinzip allein die Richtung? Die Summe der Elementarwellen hängt von Informationen über die Wellenfront ab.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Der Punkt ist doch gerade, daß du nicht weißt, wie genau diese Summe "aller" Elementarwellen aussieht, ohne jegliche Kentniss des Verlaufs der Wellenfront zu haben. Im Video wird ab Minute 7:55 behauptet, daß nun "alle" Elementarwellen in Betracht gezogen werden. Die Einhüllende der Summe liegt aber eben nicht senkrecht zur Ausbreitungsrichtung. Woher soll man nun wissen, daß dies nicht korrekt ist? |
Wie gesagt: es geht um die äußere Einhüllende zu einem beliebigen Zeitpunkt (wie es im Video auch vorher gezeigt). Damit wird es dann auch eindeutig. |
Das beantwortet doch die Frage nicht. Woher weißt du, daß die vorher im Video gezeigte Summe richtig ist und die ab 8:00 gezeigte Summe falsch? Weil du die korrekte Ausbreitungsrichtung kennst?
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 22. Feb 2020 20:30 Titel: Nils Hoppenstedt Verfasst am: 22. Feb 2020 20:30 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Das beantwortet doch die Frage nicht. Woher weißt du, daß die vorher im Video gezeigte Summe richtig ist und die ab 8:00 gezeigte Summe falsch? |
Es ist zwar richtig, dass die eingezeichneten roten Linien jeweils durch die Wellenberge der Elementarwellen gehen, aber keine dieser Linien ist die äußere Einhüllende des gesamten Wellenfeldes, da es ja hinter jeder Linie noch weitere Elementarwellenkreise gibt. Dies ist bei der (richtigen) Konstruktion bei Minute 7:30 anders. Hier gibt es hinter der vordersten der roten Linien keine weiteren Elementarwellenkreise. Sie ist also tatsächlich die äußere Einhüllende und beschreibt damit eindeutig die neue Wellenfront und damit die neue Ausbreitungsrichtung. Genau das ist das Huygensche Prinzip.
Edit: Vielleicht sollte man noch dazu sagen, dass in der Darstellung in Minute 8:00 nicht alle Elementarkreiswellen eingezeichnet sind. Die Welle trifft die Grenzfläche ja zu erst unten und erst etwas später oben. Im Medium sollte also zu einem gegebenen Zeitpunkt im unteren Bereich mehr Kreiswellen zu sehen sein.
Zuletzt bearbeitet von Nils Hoppenstedt am 22. Feb 2020 21:25, insgesamt einmal bearbeitet |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 22. Feb 2020 21:16 Titel: index_razor Verfasst am: 22. Feb 2020 21:16 Titel: |
 |
|
| Nils Hoppenstedt hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Das beantwortet doch die Frage nicht. Woher weißt du, daß die vorher im Video gezeigte Summe richtig ist und die ab 8:00 gezeigte Summe falsch? |
Es ist zwar richtig, dass die eingezeichneten roten Linien jeweils durch die Wellenberge der Elementarwellen gehen, aber keine dieser Linien ist die äußere Einhüllende des gesamten Wellenfeldes, da es ja hinter jeder Linie noch weitere Elementarwellenkreise gibt.
|
Schau mal bei Minute 8:23. Warum sind die eingezeichneten roten Linien nicht die korrekten Wellenzüge? Eine davon liegt genau auf der Einhüllenden der eingezeichneten Elementarwellen. Die müßte also nach deinem Argument die korrekte Wellenfront sein. Es sei denn du kannst begründen, daß die Summe dort falsch ist. Das hast du bis jetzt nicht getan. Und das kannst du m.E. auch nicht auf Basis des Huygenschen Prinzips allein.
| Zitat: |
Dies ist bei der (richtigen) Konstruktion bei Minute 7:30 anders. Hier gibt es hinter der vordersten der roten Linien keine weiteren Elementarwellenkreise. Sie ist also tatsächlich die äußere Einhüllende und beschreibt damit eindeutig die neue Wellenfront und damit die neue Ausbreitungsrichtung. Genau das ist das Huygensche Prinzip. |
Ich finde du argumentierst immer noch völlig an der Behauptung im Video vorbei. Versuchen wir es mal so: Das Huygensche Prinzip ist eine Konsequenz der Wellengleichung und von ein paar Integralidentitäten. Es gilt für alle Wellenformen, beliebige Oberflächen und alle möglichen Ausbreitungsrichtungen. Das Brechungsgesetz ist hingegen (wie im Video erklärt) ein Resultat der unterschiedlichen dielektrischen Eigenschaften der Medien. Keine dieser Eigenschaften geht in das Huygensche Prinzip ein außer implizit über die zu berechnende Welle. Es ist genauso anwendbar wenn sich auf beiden Seiten der eingezeichneten Oberfläche dasselbe Medium befindet und folglich keinerlei Brechung stattfindet.
Mathematisch gesehen mußt du für die Berechnung der Summe der Elementarwellen die Normalenableitung der Welle auf der Grenzfläche kennen. Es ist doch klar, daß dies nur dann durchführbar ist, wenn du schon weißt in welche Richtung sich die Welle nach Durchqueren der Grenzfläche ausbreitet. Das Huygensche Prinzip sagt dir das nicht.
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 22. Feb 2020 21:29 Titel: Nils Hoppenstedt Verfasst am: 22. Feb 2020 21:29 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: |
Schau mal bei Minute 8:23. Warum sind die eingezeichneten roten Linien nicht die korrekten Wellenzüge? Eine davon liegt genau auf der Einhüllenden der eingezeichneten Elementarwellen. Die müßte also nach deinem Argument die korrekte Wellenfront sein. Es sei denn du kannst begründen, daß die Summe dort falsch ist. Das hast du bis jetzt nicht getan. Und das kannst du m.E. auch nicht auf Basis des Huygenschen Prinzips allein.
|
Siehe mein Edit von oben. Ja, die Darstellung ist falsch, da Kreiswellen weggelassen wurden.
| index_razor hat Folgendes geschrieben: |
Mathematisch gesehen mußt du für die Berechnung der Summe der Elementarwellen die Normalenableitung der Welle auf der Grenzfläche kennen. Es ist doch klar, daß dies nur dann durchführbar ist, wenn du schon weißt in welche Richtung sich die Welle nach Durchqueren der Grenzfläche ausbreitet. Das Huygensche Prinzip sagt dir das nicht. |
Es genügt, wenn die Wellenfront zu einem bestimmen Zeitpunkt bekannt ist. Mit dem Huygenschen Prinzip kann man die Wellenfront zu beliebigen späteren Zeitpunkten berechnen.
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 22. Feb 2020 21:35 Titel: index_razor Verfasst am: 22. Feb 2020 21:35 Titel: |
 |
|
| Nils Hoppenstedt hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: |
Schau mal bei Minute 8:23. Warum sind die eingezeichneten roten Linien nicht die korrekten Wellenzüge? Eine davon liegt genau auf der Einhüllenden der eingezeichneten Elementarwellen. Die müßte also nach deinem Argument die korrekte Wellenfront sein. Es sei denn du kannst begründen, daß die Summe dort falsch ist. Das hast du bis jetzt nicht getan. Und das kannst du m.E. auch nicht auf Basis des Huygenschen Prinzips allein.
|
Siehe mein Edit von oben. Ja, die Darstellung ist falsch, da Kreiswellen weggelassen wurden.
|
Wieso? Im Vergleich zu der von dir als richtig bezeichneten Darstellung wurden doch welche hinzugefügt. Tatsächlich muß auch von jedem Punkt der Fläche eine Elementarwelle ausgehen.
| Zitat: |
| index_razor hat Folgendes geschrieben: |
Mathematisch gesehen mußt du für die Berechnung der Summe der Elementarwellen die Normalenableitung der Welle auf der Grenzfläche kennen. Es ist doch klar, daß dies nur dann durchführbar ist, wenn du schon weißt in welche Richtung sich die Welle nach Durchqueren der Grenzfläche ausbreitet. Das Huygensche Prinzip sagt dir das nicht. |
Es genügt, wenn die Wellenfront zu einem bestimmen Zeitpunkt bekannt ist.
|
Nein, das genügt nicht. Ein Gegenbeispiel habe ich doch genannt.
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 22. Feb 2020 21:40 Titel: Nils Hoppenstedt Verfasst am: 22. Feb 2020 21:40 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: |
Wieso? Im Vergleich zu der von dir als richtig bezeichneten Darstellung wurden doch welche hinzugefügt.
|
Ja, aber die Anzahl der eingezeichneten Kreiswellen stimmt nicht. Hier wurden zu jedem Punkt gleich viele Kreise eingezeichnet. Die unteren Punkte wurden aber früher angeregt, hier müssten also mehr Kreise da sein. (Vergleiche die Darstellung bei Minute 7:30, hier ist es richtig)
| index_razor hat Folgendes geschrieben: |
Nein, das genügt nicht. Ein Gegenbeispiel habe ich doch genannt. |
Nein, das hast du lediglich behauptet...
Zuletzt bearbeitet von Nils Hoppenstedt am 22. Feb 2020 21:48, insgesamt einmal bearbeitet |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 22. Feb 2020 21:46 Titel: index_razor Verfasst am: 22. Feb 2020 21:46 Titel: |
 |
|
| Nils Hoppenstedt hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: |
Wieso? Im Vergleich zu der von dir als richtig bezeichneten Darstellung wurden doch welche hinzugefügt.
|
Ja, aber die Anzahl der eingezeichneten Kreiswellen stimmt nicht. Hier wurden zu jedem Punkt gleich viele Kreise eingezeichnet. Die unteren Punkte wurden aber früher angeregt, hier müssten also mehr Kreise da sein.
|
Daraus folgt immer noch nicht, daß sich die Ausbreitungsrichtung ändert.
| Zitat: |
| index_razor hat Folgendes geschrieben: |
Nein, das genügt nicht. Ein Gegenbeispiel habe ich doch genannt. |
Nein, das hast du lediglich behauptet... |
Nimm auf beiden Seiten der Grenzfläche dasselbe Medium. Dann ist die Wellenfront auf der Flläche in beiden Situationen gleich. Aber es findet keine Brechung statt.
Du behauptest hier die ganze Zeit, du könntest das Brechungsgesetz aus dem Huygenschen Prinzip ableiten. Gezeigt hast du das bis jetzt aber auch nicht.
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 22. Feb 2020 21:54 Titel: Nils Hoppenstedt Verfasst am: 22. Feb 2020 21:54 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: |
Daraus folgt immer noch nicht, daß sich die Ausbreitungsrichtung ändert.
|
Natürlich. Siehe Minute 7:30, wo die Anzahl der Kreise und damit die Einhüllende korrekt eingezeichnet wird.
| index_razor hat Folgendes geschrieben: |
Du behauptest hier die ganze Zeit, du könntest das Brechungsgesetz aus dem Huygenschen Prinzip ableiten. Gezeigt hast du das bis jetzt aber auch nicht. |
Das findet man nun wirklich tonnenweise im Netz. Hier ist ein random Link:
https://www.toppr.com/guides/physics/wave-optics/refraction-and-reflection-of-waves-using-huygens-principle/
(habs nur kurz überflogen, aber ich denke es ist korrekt.)
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 23. Feb 2020 09:20 Titel: index_razor Verfasst am: 23. Feb 2020 09:20 Titel: |
 |
|
| Nils Hoppenstedt hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: |
Daraus folgt immer noch nicht, daß sich die Ausbreitungsrichtung ändert.
|
Natürlich. Siehe Minute 7:30, wo die Anzahl der Kreise und damit die Einhüllende korrekt eingezeichnet wird.
|
Daß dies korrekt ist, folgt nicht aus dem Huygenschen Prinzip, sondern aus den Maxwellgleichungen. Alle im Video eingezeichneten Wellenfronten -- und noch unendlich viele nicht eingezeichnete -- sind mit dem Huygenschen Prinzip vereinbar. Das ist genau der Punkt.
Wenn die "korrekte" Summe der Elementarwellen durch die zeitliche Folge der Anregungen auf der Grenzfläche bestimmt wäre, wie du behauptest, dann wäre der Brechungswinkel nur vom Einfallswinkel abhängig und nicht vom Brechungsindex. Natürlich ist das nicht der Fall und die Summe hängt auch vom Verlauf des Wellenfeldes ab.
Tatsächlich hat die Begründung des Brechungsgesetzes nicht das geringste mit der Einhüllenden der Elementarwellen zu tun. Diese Behauptung hast du komplett aus der Luft gegriffen. Das Brechungsgesetz ist exakt dasselbe, wenn du komplett monochromatische Wellen betrachtest, die zu allen Zeiten überall auf ihrer Seite der Halbebene waren. (Streng genommen bezieht sich das Gesetz auch nur auf diesen Fall, da ja eine Frequenzabhängigkeit von n nicht ausgeschlossen ist.) Deshalb ist auch deine Behauptung, die ab 7:55 eingezeichneten Elementarwellen resultierten aus eine falschen Anwendung des Huygenschen Prinzips, völlig unbegründet.
Deine Behauptung war aber, daß du mit Hilfe des Huygenschen Prinzips aus der Kenntnis des Wellenfeldes auf der Grenzfläche den Brechungswinkel ableiten könntest. Das bringt dein random link, wenig überraschenderweise, natürlich auch nicht fertig.
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 23. Feb 2020 11:31 Titel: Nils Hoppenstedt Verfasst am: 23. Feb 2020 11:31 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: |
Daß dies korrekt ist, folgt nicht aus dem Huygenschen Prinzip, sondern aus den Maxwellgleichungen.
|
Langsam wird es albern, an dieser Stelle ist von den Maxwellgleichungen doch noch überhaupt nicht die Rede.
| index_razor hat Folgendes geschrieben: |
Wenn die "korrekte" Summe der Elementarwellen durch die zeitliche Folge der Anregungen auf der Grenzfläche bestimmt wäre, wie du behauptest, dann wäre der Brechungswinkel nur vom Einfallswinkel abhängig und nicht vom Brechungsindex.
|
Sorry, du hast dich da echt in was verrannt. In dem Link oben wird es doch explizit vorgerechnet, inklusive der Abhängigkeit vom Brechungsindex. Tatsächlich ist das Schulstoff.... wenn du das immer noch nicht einsiehst, dann kann ich dir leider echt nicht weiterhelfen. Oder könnte es sein, dass dir überhaupt nicht so richtig klar ist, worum es beim Huygenschen Prinzip geht?
| index_razor hat Folgendes geschrieben: |
Das Brechungsgesetz ist exakt dasselbe, wenn du komplett monochromatische Wellen betrachtest, die zu allen Zeiten überall auf ihrer Seite der Halbebene waren.
|
Ich hab keine Ahnung, was du damit sagen willst...
| index_razor hat Folgendes geschrieben: |
(Streng genommen bezieht sich das Gesetz auch nur auf diesen Fall, da ja eine Frequenzabhängigkeit von n nicht ausgeschlossen ist.)
|
Bei einer monochromatischen Welle ändert sich die Frequenz doch überhaupt nicht beim Übertritt in das neue Medium. Ich schlage vor, du beschäftigst dich erstmal mit den Grundlagen, mittlerweile geht hier ja alles durcheinander.
| index_razor hat Folgendes geschrieben: |
Deine Behauptung war aber, daß du mit Hilfe des Huygenschen Prinzips aus der Kenntnis des Wellenfeldes auf der Grenzfläche den Brechungswinkel ableiten könntest. Das bringt dein random link, wenig überraschenderweise, natürlich auch nicht fertig. |
Nein, meine Behauptung war, dass man die neue Ausbreitungsrichtung im 2. Medium mit Hilfe des Huygenschen Prinzips alleine aus der Kenntnis der Lage der Wellenfronten im 1. Medium herleiten kann. Eben genauso wie es im Link gemacht wird. Wie gesagt, das ist Schulstoff (ganz ohne Maxwellgleichungen). Ich verstehe ehrlich gesagt nicht, wieso du immer noch behauptest, dass das nicht geht und "überhaupt nichts dem Huygenschen Prinzip" zu tun hat, wo es doch hier explizit vorgerechnet wird.
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 23. Feb 2020 12:39 Titel: index_razor Verfasst am: 23. Feb 2020 12:39 Titel: |
 |
|
| Nils Hoppenstedt hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: |
Daß dies korrekt ist, folgt nicht aus dem Huygenschen Prinzip, sondern aus den Maxwellgleichungen.
|
Langsam wird es albern, an dieser Stelle ist von den Maxwellgleichungen doch noch überhaupt nicht die Rede.
|
Ja eben. Weil du nur von Huygens redest und nicht von Maxwell folgt deine Behauptung ja auch nicht.
| Zitat: |
| index_razor hat Folgendes geschrieben: |
Wenn die "korrekte" Summe der Elementarwellen durch die zeitliche Folge der Anregungen auf der Grenzfläche bestimmt wäre, wie du behauptest, dann wäre der Brechungswinkel nur vom Einfallswinkel abhängig und nicht vom Brechungsindex.
|
Sorry, du hast dich da echt in was verrannt. In dem Link oben wird es doch explizit vorgerechnet, inklusive der Abhängigkeit vom Brechungsindex.
|
Dort wird ein Zusammenhang zwischen Ausbreitungsgeschwindigkeit und Brechungsindex angenommen. Der folgt aus den Maxwellgleichungen. Aus diesen folgt auch direkt das Brechungsgesetz. Aus dem Huygenschen Prinzip allein folgt gar nichts.
| Zitat: |
| Zitat: |
Das Brechungsgesetz ist exakt dasselbe, wenn du komplett monochromatische Wellen betrachtest, die zu allen Zeiten überall auf ihrer Seite der Halbebene waren.
|
Ich hab keine Ahnung, was du damit sagen willst...
|
Daß deine Aussagen über die Einhüllende irrelevant sind. Zumindest sehe ich nicht, wie du in diesem Fall eine Einhüllende bestimmen willst.
| Zitat: |
| index_razor hat Folgendes geschrieben: |
(Streng genommen bezieht sich das Gesetz auch nur auf diesen Fall, da ja eine Frequenzabhängigkeit von n nicht ausgeschlossen ist.)
|
Bei einer monochromatischen Welle ändert sich die Frequenz doch überhaupt nicht beim Übertritt in das neue Medium.
|
Na und?
| Zitat: |
Ich schlage vor, du beschäftigst dich erstmal mit den Grundlagen, mittlerweile geht hier ja alles durcheinander.
|
Ich schlage vor, du kommst mal wieder auf den Teppich. Keine Ahnung was dir hier so zu Kopf steigt, aber so vollkommen gerechtfertigt scheint mir dein überheblicher Tonfall nicht zu sein.
| Zitat: |
| index_razor hat Folgendes geschrieben: |
Deine Behauptung war aber, daß du mit Hilfe des Huygenschen Prinzips aus der Kenntnis des Wellenfeldes auf der Grenzfläche den Brechungswinkel ableiten könntest. Das bringt dein random link, wenig überraschenderweise, natürlich auch nicht fertig. |
Nein, meine Behauptung war, dass man die neue Ausbreitungsrichtung im 2. Medium mit Hilfe des Huygenschen Prinzips alleine aus der Kenntnis der Lage der Wellenfronten im 1. Medium herleiten kann.
|
Und das ist und bleibt falsch. Wenn das so wäre, könnte die Richtung im 2. Medium ja nicht vom Brechungsindex abhängen.
| Zitat: |
Eben genauso wie es im Link gemacht wird. Wie gesagt, das ist Schulstoff (ganz ohne Maxwellgleichungen).
|
Nein, du benötigst Annahmen, die nur aus den Maxwellgleichungen folgen, nicht aus dem Huygenschen Prinzip. Diese Annahmen verwendet auch dein link. Genau das ist die Behauptung.
***
P.S. noch was zu der Relevanz deines Links. Die Behauptung im Video ist ja, daß die Folgerungen aus dem Huygenschen Prinzip nicht eindeutig sind, wenn man tatsächlich alle Elementarwellen aufsummiert. In der Rechnung im Link wird genau eine Elementarwelle geeignet ausgewählt. Das widerlegt natürlich nicht die Behauptung im Video. Selbstverständlich gibt es eine korrekte Summatation der Elementarwellen, so daß das Ergebnis im Einklang mit dem Brechungsgesetz ist. Der Punkt ist nur, daß nicht auf Basis des Prinzips allein festliegt, wie diese Summe auszuführen ist. Mathematisch ist das klar: die Summe beinhaltet Informationen über die Änderung des Wellenfeldes an der Grenzfläche. Das widerlegt m.E. auch nochmal deine Behauptung du könntest das Feld auf der einen Seite der Grenzfläche allein aus seinem Wert auf der anderen Seite ausrechnen.
Zuletzt bearbeitet von index_razor am 23. Feb 2020 13:07, insgesamt einmal bearbeitet |
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 23. Feb 2020 12:59 Titel: Nils Hoppenstedt Verfasst am: 23. Feb 2020 12:59 Titel: |
 |
|
|
Ich denke, an dieser Stelle hat die Diskussion einen Punkt erreicht, wo wir nicht mehr weiter kommen.
|
|
 |
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3419
|
 ML Verfasst am: 23. Feb 2020 14:20 Titel: ML Verfasst am: 23. Feb 2020 14:20 Titel: |
 |
|
Hallo,
| index_razor hat Folgendes geschrieben: |
Du behauptest hier die ganze Zeit, du könntest das Brechungsgesetz aus dem Huygenschen Prinzip ableiten. Gezeigt hast du das bis jetzt aber auch nicht. |
vielleicht kannst Du ja mal genauer definieren, was bei der Erklärung mit dem Huygens'schen Prinzip fehlt. Das würde die Diskussion weiterbringen.
Es kann ja sein, dass noch etwas Subtiles fehlt. Aber der Hinweis aus dem Video, einzig die Maxwellgleichungen seien geeignet, das Brechungsgesetz zu erklären, ist nicht wirklich befriedigend.
Es ist richtig, dass die Maxwellgleichungen zusammen mit den Anfangs- und Randbedingungen sowie den Materialeigenschaften die Brechung von Licht korretk beschreiben. Aber woher bist Du Dir so sicher, dass die Kenntnis über die einlaufende Wellenfront, die Lichtgeschwindigkeiten in beiden Medien und die Annahme von Kugelwellen nicht ebenso ausreichen?
Die unterschiedlichen Gleichungen können ja durchaus Redundanz enthalten.
Ich frage deshalb so explizit, da das Brechungsgesetz von Snellius in ähnlicher Form auch für Schallwellen gilt. Exakt gilt es bei ebenen Wellen an einer ebenen Grenzfläche zwischen zwei mit einem Fluid gefüllten Halbräumen.
Es ist klar, dass es in beiden Gebieten auch bei angenommener Linearität mehr gibt als nur "Snellius" (Licht: Polarisation, Doppelbrechung; Schall: Modenwandlungen zwischen Longitudinal-, Transversal- und Oberflächenwellen u. ä.), aber im einfachsten Fall sind die Green'schen Funktionen zumindest bei Schall Kugelwellen, die von der Grenzfläche der Medien ausgehen.
In der Praxis verwendet man nicht selten (mit Übereinstimmung zwischen Simulation und Messung) eine sogenannte Punktquellensynthese, um die Fokussiereigenschaften von akustischen Linsen oder die Schallfelder bei der Ansteuerung von Ultraschallarrays zu berechnen. Im Bild ist ein einstufiges Verfahren gezeigt, bei dem man das Schallfeld in einem Fluid als Ergebnis der mechanischen Spannung an der Grenzfläche berechnen kann.
Viele Grüße
Michael
| Beschreibung: |
|

Download |
| Dateiname: |
Bild.png |
| Dateigröße: |
81.52 KB |
| Heruntergeladen: |
148 mal |
|
|
 |
Qubit
Anmeldungsdatum: 17.10.2019
Beiträge: 851
|
 Qubit Verfasst am: 23. Feb 2020 14:39 Titel: Qubit Verfasst am: 23. Feb 2020 14:39 Titel: |
 |
|
Huygens-Fresnel bietet ein geometrisch-kinematisches Modell für Lösungen der Maxwellgleichungen (allg. Wellengleichungen). Das Prinzip an sich (Aufsummieren von Amplituden und Phasen von Wavelets) ist bei vielen Berechnungen (und Kostruktionen wie zB. Fresnelsche Zonen) als Modell hinreichend. Will man es aber theoretisch fundieren, dann muss es an entsprechenden Stellen erweitert werden (Kirchhoff, Sommerfeld).
Siehe zB.
https://aapt.scitation.org/doi/10.1119/1.12882
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 23. Feb 2020 15:22 Titel: index_razor Verfasst am: 23. Feb 2020 15:22 Titel: |
 |
|
| ML hat Folgendes geschrieben: |
| index_razor hat Folgendes geschrieben: |
Du behauptest hier die ganze Zeit, du könntest das Brechungsgesetz aus dem Huygenschen Prinzip ableiten. Gezeigt hast du das bis jetzt aber auch nicht. |
vielleicht kannst Du ja mal genauer definieren, was bei der Erklärung mit dem Huygens'schen Prinzip fehlt. Das würde die Diskussion weiterbringen.
Es kann ja sein, dass noch etwas Subtiles fehlt. Aber der Hinweis aus dem Video, einzig die Maxwellgleichungen seien geeignet, das Brechungsgesetz zu erklären, ist nicht wirklich befriedigend.
|
Ich halte das nicht für subtil. Das Video enthält mehrere Hinweise darauf warum die "Summe der Elementarwellen" mehrdeutig ist. Wenn ich mir das Helmholtz-Integral anschaue, finde ich das eigentlich auch einleuchtend
=\frac{1}{4\pi}\int \frac{e^{ikr_x}}{r_x}\nabla u(r) - u(r)\nabla\left(\frac{e^{ikr_x}}{r_x}\right)\dd \vec{S})
Kurz gesagt, man summiert nicht einfach nur Elementarwellen, sondern in Abhängigkeit vom weiteren Verlauf der Welle gewichtete Elementarwellen. Diese nötige Zusatzinformation folgt nicht aus dem Huygenschen Prinzip und wenn man sie einbauen will, um tatsächlich etwas vorherzusagen, benötigt man plausible Annahmen, z.B für  . Wo sollen die herkommen, wenn nicht ultimativ aus den Maxwellgleichungen? Und wenn ich dann schon weiß, wie die Normalableitung aussieht, benötige ich dann noch das Huygensche Prinzip? Das erscheint mir einfach zirkulär. . Wo sollen die herkommen, wenn nicht ultimativ aus den Maxwellgleichungen? Und wenn ich dann schon weiß, wie die Normalableitung aussieht, benötige ich dann noch das Huygensche Prinzip? Das erscheint mir einfach zirkulär.
| Zitat: |
Es ist richtig, dass die Maxwellgleichungen zusammen mit den Anfangs- und Randbedingungen sowie den Materialeigenschaften die Brechung von Licht korretk beschreiben. Aber woher bist Du Dir so sicher, dass die Kenntnis über die einlaufende Wellenfront, die Lichtgeschwindigkeiten in beiden Medien und die Annahme von Kugelwellen nicht ebenso ausreichen?
|
Das habe ich, glaube ich, gar nicht behauptet. Ich sehe es aber so, daß diese ganzen Zusatzannahmen 1) nicht aus dem Huygenschen Prinzip folgen und es 2) ziemlich entbehrlich zu machen scheinen. In welchem Sinne liefert es also eine Erklärung für Brechung? Um diese Frage ging es doch in dem Video.
| Zitat: |
Ich frage deshalb so explizit, da das Brechungsgesetz von Snellius in ähnlicher Form auch für Schallwellen gilt. Exakt gilt es bei ebenen Wellen an einer ebenen Grenzfläche zwischen zwei mit einem Fluid gefüllten Halbräumen.
Es ist klar, dass es in beiden Gebieten auch bei angenommener Linearität mehr gibt als nur "Snellius" (Licht: Polarisation, Doppelbrechung; Schall: Modenwandlungen zwischen Longitudinal-, Transversal- und Oberflächenwellen u. ä.), aber im einfachsten Fall sind die Green'schen Funktionen zumindest bei Schall Kugelwellen, die von der Grenzfläche der Medien ausgehen.
|
Ja natürlich. Aber die Greensfunktionen sind doch immer Kugelwellen, auch wenn ich entlang von Flächen summiere, durch die gar keine Mediengrenze verläuft. Die Form der Greensfunktionen reicht also als Erklärung nicht aus. Das Huygensche Prinzip ist doch eine rein geometrische Identität. Ohne Randbedingungen folgt daraus nicht viel. Und diese Randbedingungen, nicht das Huygensche Prinzip, sind doch genau die Information, die man für das Brechungsgesetz benötigt.
|
|
 |
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3419
|
 ML Verfasst am: 24. Feb 2020 00:16 Titel: ML Verfasst am: 24. Feb 2020 00:16 Titel: |
 |
|
Hallo,
| index_razor hat Folgendes geschrieben: |
Ich halte das nicht für subtil. Das Video enthält mehrere Hinweise darauf warum die "Summe der Elementarwellen" mehrdeutig ist.
|
Du meinst die ebenfalls als möglich bezeichnete Ausbreitung gemäß Bild 1?
Diesen Ansatz habe ich (um ehrlich zu sein: ohne genaueres Nachdenken) immer gleich verworfen, weil ich mir gedacht habe, dass die Welle sich nicht gewissermaßen "selbst überholen" kann.
Schülern gebe ich hierzu folgenden Hinweis:
Man bilde im 2. Medium jeweils die Tangente an den Ringen, die durch die selbe Wellenfront des 1. Mediums erzeugt wurden.
- Im Beispiel von Bild 2 bedeutet das, dass direkt am Berührpunkt der vordersten Wellenfront mit der Grenzfläche der 0. Ring (=Punkt an der Grenzfläche) verwendet werden soll.
- Von den Wellen, die vom Schnittpunkt der zweitvordersten Wellenfront des Ausgangsmediums mit der Grenzfläche ausgehen, muss man den 1. Ring verwenden, da dieser "vor einer Wellenlänge/Periodendauer", also von der vordersten Wellenfront, angeregt wurde.
- Von den Wellen, die vom Schnittpunkt der drittvordersten Wellenfront des Ausgangsmediums mit der Grenzfläche ausgehen, muss man den 2. Ring verwenden, da dieser "vor zwei Wellenlängen/Perdiodendauern", also wiederum von der vordersten Wellenfront angeregt worden war.
usw.
Dein Einwand macht mich aber ehrlich gesagt schon nachdenklich. Das Auswahlkritium führt zwar zu richtigen Lösungen, aber die Erklärungskraft ist nicht so groß wie ich ursprünglich dachte.
Vor allem bleibt bei der Betrachtung dieser Wellenfronten vollkommen außer acht, welche Amplituden vorliegen und (das kritisiert das Video ja zurecht) in welche Richtung die Energie sich ausbreitet.
| Zitat: |
Und wenn ich dann schon weiß, wie die Normalableitung aussieht, benötige ich dann noch das Huygensche Prinzip? Das erscheint mir einfach zirkulär.
|
Wir sind uns einig, dass das Huygens'sche Prinzip letztlich nur ein Modell dafür ist, wie die Wellen überhaupt zum Laufen kommen. Es liefert im besten Fall redundante Informationen (die die Maxwellgleichungen auch so liefern würden) und verleitet darüber hinaus -- wie wir am Beispiel sehen -- zu unvollständigen Erklärungen.
Die Verwendung von zusätzlichen, redundanten Gleichungen ist in der Physikdidaktik aber auch nichts wirklich Außergewöhnliches. Ich meine hier beispielsweise die Nutzung des Energieerhaltungssatzes zusätzlich zu einem Theoriegebäude wie dem System der Maxwellgleichungen.
| Zitat: |
Ja natürlich. Aber die Greensfunktionen sind doch immer Kugelwellen,
|
Beim Schall stimmt das nicht mehr so richtig (siehe Bild 3) -- allerdings führt uns das von der eigentlichen Diskussion weg.
Grund für die komische Form der Punktrichtcharakteristik beim Übergang PZT-Wasser ist, dass Modenwandlungen und Oberflächenwellen mit in die Richtcharakteristik mit eingehen. Erstaunlich beim Beispiel PZT--Wasser ist aber, dass diese Punktrichtcharakteristik sich bei praktischen Anwendungen mit halbwegs großen Schallwandlerelementen nur wenig auf das Gesamtschallfeld auswirken.
| Zitat: |
Die Form der Greensfunktionen reicht also als Erklärung nicht aus.
|
Ja, das stimmt. Sie liefert nur eine Teilinformation. Aber durch die Abstände der Wellenfronten lassen wir indirekt auch die Lichtgeschwindigkeiten eingehen.
| Zitat: | | Das Huygensche Prinzip ist doch eine rein geometrische Identität. Ohne Randbedingungen folgt daraus nicht viel. Und diese Randbedingungen, nicht das Huygensche Prinzip, sind doch genau die Information, die man für das Brechungsgesetz benötigt. |
Ja, da stimme ich zu.
Schauen wir nochmal, was in der Snellius-Gleichung drinsteht:
1.) die Lichtgeschwindigkeiten in beiden Medien und
2.) der Einfallswinkel in beiden Medien
Die Lichtgeschwindigkeiten gehen bei dem Huygens'schen Ansatz mit ein, da wir die Abstände der Wellenfronten entsprechend den jeweiligen Wellenlängen (und damit: Lichtgeschwindigkeiten) wählen.
Die Winkel gehen aber nur ein, wenn wir Auswahlkriterien für die "richtigen" Wellenfronten (wie von mir weiter oben beschrieben) mit einführen. Diese Auswahlkritien sind m. E. aber noch nicht ausreichend begründet und werden bei der Erklärung irgendwie mit "hineingeschummelt".
Viele Grüße
Michael
| Beschreibung: |
|

Download |
| Dateiname: |
Bild1.jpg |
| Dateigröße: |
77 KB |
| Heruntergeladen: |
137 mal |
| Beschreibung: |
|

Download |
| Dateiname: |
Bild2.jpg |
| Dateigröße: |
131.03 KB |
| Heruntergeladen: |
129 mal |
| Beschreibung: |
|

Download |
| Dateiname: |
Bild3.jpg |
| Dateigröße: |
75.01 KB |
| Heruntergeladen: |
145 mal |
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 26. Feb 2020 20:41 Titel: index_razor Verfasst am: 26. Feb 2020 20:41 Titel: |
 |
|
| ML hat Folgendes geschrieben: |
| index_razor hat Folgendes geschrieben: |
Ich halte das nicht für subtil. Das Video enthält mehrere Hinweise darauf warum die "Summe der Elementarwellen" mehrdeutig ist.
|
Du meinst die ebenfalls als möglich bezeichnete Ausbreitung gemäß Bild 1?
|
Ja, unter anderem die meine ich. Ich bin mir aber noch nicht im Klaren darüber, ob das tatsächlich am Huygensschen Prinzip liegt -- das Problem also unterbestimmt ist -- oder ob lediglich die Anwendung mit ausschließlich elementargeometrischen Methoden mehrdeutig ist. Auf jeden Fall sehe ich keinen offensichtlichen Fehler in den Argumenten im Video, die zu den anderen Resultaten führen; zumindest keine, die sich mit dem Huygensschen Prinzip und auf Basis derselben Methoden allein begründen ließen.
| Zitat: |
Diesen Ansatz habe ich (um ehrlich zu sein: ohne genaueres Nachdenken) immer gleich verworfen, weil ich mir gedacht habe, dass die Welle sich nicht gewissermaßen "selbst überholen" kann.
Schülern gebe ich hierzu folgenden Hinweis:
Man bilde im 2. Medium jeweils die Tangente an den Ringen, die durch die selbe Wellenfront des 1. Mediums erzeugt wurden.
|
Das ist auch sicher eine sinnvolle Konstruktion. Aber folgt sie aus dem Huygensschen Prinzip? Laut diesem Prinzip ergibt sich die resultierende Welle als Summe aller Elementarwellen über die gesamte Oberfläche. Wie genau führe ich diese Summe mit elementaren Methoden aus? Und was sind "alle" Elementarwellen? (Diese Frage wirft das Video ja auch auf.) Ich kann lediglich bestimmen, daß alle Punkte, in denen sich "gleich viele" Elementarwellen schneiden, dieselbe Amplitude haben. Das sieht erstmal, wie Dr. Don feststellt, mehrdeutig aus.
Ich kann natürlich versuchen mit Plausibilitätsbetrachtungen über die zeitlichen Reihenfolge der Elementaranregungen ein eindeutiges Ergebnis zu erhalten. Aber dieses Argument scheint mir irgendwie trügerisch zu sein. Bei der Ableitung des Brechungsgesetzes aus den Maxwellgleichungen betrachten wir normalerweise ebene monochromatische Wellen. Deren Gleichungen lassen sich vollkommen auf den stationären Fall zurückführen, d.h. die Zeitabhängigkeit fällt raus. Von ihr hängt das Resultat also nicht ab. Wieso sollte sie also bei der Herleitung gerade die entscheidende Rolle spielen? Ist das nicht unlogisch?
Monochromatische Wellen erfüllen die Helmholtzgleichung u(x)=0) . In diesem Fall nimmt das Huygens-Prinzip die präzise Form des Kirchhoff-Helmholtz-Integrals aus meinem vorigen Beitrag an. Ich denke man kann das Problem nun so formulieren: Unter welchen Bedingungen an u gilt die speziellere Form . In diesem Fall nimmt das Huygens-Prinzip die präzise Form des Kirchhoff-Helmholtz-Integrals aus meinem vorigen Beitrag an. Ich denke man kann das Problem nun so formulieren: Unter welchen Bedingungen an u gilt die speziellere Form
 = \frac{1}{4\pi} \int_S \frac{e^{ik|r-x|}}{|r-x|}\nabla u(r)\cdot \dd\vec{S}\quad \text{(1)})
Dieses Integral sieht mir wie eine mathematische Präzisierung der elementargeometrsichen Konstruktion aus. Danach ist ) zumindest eindeutig aus zumindest eindeutig aus 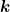 und und  bestimmt. Es zeigt auch nochmal explizit, daß die Eindeutigkeit gar nichts mit der zeitlichen Reihenfolge der Anregungen zu tun hat, da die Zeit ja nirgendwo eingeht. Es kann natürlich sein, daß die nötigen Voraussetzungen für (1) bereits implizit im Helmholtz-Integral enthalten sind. (Eine ähnliche Situation liegt ja auch bei den Greenschen Identitäten in der Elektrostatik vor.) bestimmt. Es zeigt auch nochmal explizit, daß die Eindeutigkeit gar nichts mit der zeitlichen Reihenfolge der Anregungen zu tun hat, da die Zeit ja nirgendwo eingeht. Es kann natürlich sein, daß die nötigen Voraussetzungen für (1) bereits implizit im Helmholtz-Integral enthalten sind. (Eine ähnliche Situation liegt ja auch bei den Greenschen Identitäten in der Elektrostatik vor.)
Was mich dann aber noch stört ist, daß ich gar nicht weiß, wie ich  auswerten soll. Das ganze hängt doch von der Ausbreitungsrichtung auswerten soll. Das ganze hängt doch von der Ausbreitungsrichtung 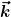 im Medium 2 ab oder? Und die soll doch gerade "berechnet" werden. Das ist es, was mir daran zirkulär vorkommt. (Oder muß ich die "linksseitige" Richtungsableitung, d.h. im Medium 1, verwenden? Dann wäre alles eindeutig bestimmt. Aber wie rechtfertige ich das?) im Medium 2 ab oder? Und die soll doch gerade "berechnet" werden. Das ist es, was mir daran zirkulär vorkommt. (Oder muß ich die "linksseitige" Richtungsableitung, d.h. im Medium 1, verwenden? Dann wäre alles eindeutig bestimmt. Aber wie rechtfertige ich das?)
| Zitat: |
| Zitat: |
Und wenn ich dann schon weiß, wie die Normalableitung aussieht, benötige ich dann noch das Huygensche Prinzip? Das erscheint mir einfach zirkulär.
|
Wir sind uns einig, dass das Huygens'sche Prinzip letztlich nur ein Modell dafür ist, wie die Wellen überhaupt zum Laufen kommen. Es liefert im besten Fall redundante Informationen (die die Maxwellgleichungen auch so liefern würden) und verleitet darüber hinaus -- wie wir am Beispiel sehen -- zu unvollständigen Erklärungen.
Die Verwendung von zusätzlichen, redundanten Gleichungen ist in der Physikdidaktik aber auch nichts wirklich Außergewöhnliches. Ich meine hier beispielsweise die Nutzung des Energieerhaltungssatzes zusätzlich zu einem Theoriegebäude wie dem System der Maxwellgleichungen.
|
Die Redundanz des Huygensschen Prinzips sehe ich auch nicht als problematisch an. Mir ist einfach nicht klar, wie ich von einer einlaufenden monochromatischen Welle auf die Richtung des Ausbreitungsvektors komme, wenn ich nur das Huygenssche Prinzip verwenden darf. Die redundanten Gleichungen, die ich noch bräuchte sind für mich die Maxwellgleichungen. Aber die machen das Huygensche Prinzip auch überflüssig.
| Zitat: |
| Zitat: |
Ja natürlich. Aber die Greensfunktionen sind doch immer Kugelwellen,
|
Beim Schall stimmt das nicht mehr so richtig (siehe Bild 3) -- allerdings führt uns das von der eigentlichen Diskussion weg.
Grund für die komische Form der Punktrichtcharakteristik beim Übergang PZT-Wasser ist, dass Modenwandlungen und Oberflächenwellen mit in die Richtcharakteristik mit eingehen. Erstaunlich beim Beispiel PZT--Wasser ist aber, dass diese Punktrichtcharakteristik sich bei praktischen Anwendungen mit halbwegs großen Schallwandlerelementen nur wenig auf das Gesamtschallfeld auswirken.
|
Hm, ich meinte mit "immer" eigentlich auch nur die Fälle, in denen die normale (3+1-dimensionale) Wellengleichung  gilt. Ich dachte unter diesen Voraussetzungen haben wir es mit Kugelwellen als Fundamentallösungen zu tun. gilt. Ich dachte unter diesen Voraussetzungen haben wir es mit Kugelwellen als Fundamentallösungen zu tun.
| Zitat: |
| Zitat: | | Das Huygensche Prinzip ist doch eine rein geometrische Identität. Ohne Randbedingungen folgt daraus nicht viel. Und diese Randbedingungen, nicht das Huygensche Prinzip, sind doch genau die Information, die man für das Brechungsgesetz benötigt. |
Ja, da stimme ich zu.
Schauen wir nochmal, was in der Snellius-Gleichung drinsteht:
1.) die Lichtgeschwindigkeiten in beiden Medien und
2.) der Einfallswinkel in beiden Medien
Die Lichtgeschwindigkeiten gehen bei dem Huygens'schen Ansatz mit ein, da wir die Abstände der Wellenfronten entsprechend den jeweiligen Wellenlängen (und damit: Lichtgeschwindigkeiten) wählen.
|
Das kann man natürlich voraussetzen. Aber ich denke das Video wollte auf eine weit spezifischere Erklärung hinaus, in welcher die Brechung mit den dielektrischen Eigenschaften des Mediums in Verbindung gebracht wird. Dann benötigt man ja noch den Zusammenhang  . Aber ist die Annahme über die Abhängigkeit der Lichtgeschwindigkeit vom Medium wirklich plausibler, als die Änderung der Ausbreitungsrichtung die man damit erklären will? . Aber ist die Annahme über die Abhängigkeit der Lichtgeschwindigkeit vom Medium wirklich plausibler, als die Änderung der Ausbreitungsrichtung die man damit erklären will?
| Zitat: |
Die Winkel gehen aber nur ein, wenn wir Auswahlkriterien für die "richtigen" Wellenfronten (wie von mir weiter oben beschrieben) mit einführen. Diese Auswahlkritien sind m. E. aber noch nicht ausreichend begründet und werden bei der Erklärung irgendwie mit "hineingeschummelt".
|
Ja, ich denke darauf können wir uns einigen.
|
|
 |
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3419
|
 ML Verfasst am: 27. Feb 2020 02:28 Titel: ML Verfasst am: 27. Feb 2020 02:28 Titel: |
 |
|
Hallo,
| index_razor hat Folgendes geschrieben: | Auf jeden Fall sehe ich keinen offensichtlichen Fehler in den Argumenten im Video, die zu den anderen Resultaten führen; zumindest keine, die sich mit dem Huygensschen Prinzip und auf Basis derselben Methoden allein begründen ließen.
|
Ich habe nochmal in das Video reingeschaut und glaube jetzt zu wissen, was da falsch läuft:
Wenn ich das richtig sehe, lässt das Video nur von den Punkten der Grenzfläche Elementarwellen ausgehen, an denen gerade ein Wellenberg ankommt. Die Punktquellen auf der Grenzfläche müssen aber eigentlich kontinuierlich absenden, und zwar von jedem (bestrahlten) Punkt der Oberfläche ausgehend.
kontinuierliche Abstrahlung heißt: Es dürfen nicht nur Wellenberge ausgesendet werden, sondern auch Wellentäler und alle Phasen dazwischen.
von jedem Punkt heißt: Die Punktdichte muss groß sein, dass zwischen zwei Punktquellen gleicher Phase noch weitere Punktquellen mit unterschiedlicher Phase liegen müssen.
| Zitat: | | Mir ist einfach nicht klar, wie ich von einer einlaufenden monochromatischen Welle auf die Richtung des Ausbreitungsvektors komme, wenn ich nur das Huygenssche Prinzip verwenden darf. |
Die Richtungsinformation über das einfallende Licht steckt letztlich in der Phasendifferenz zwischen den einzelnen Punktquellen: Wenn ein Lichtbündel senkrecht auf eine (sagen wir: plane) Glasfläche einfällt, werden alle Punkte gleichphasig angeregt. Wenn das Licht schräg von rechts einfällt, liegen Phasendifferenzen vor, weil der linke Teil des Lichtbündels eine weitere Strecke durch die Luft laufen muss als der rechte.
Die zugehörigen Phasendifferenzen bei den Punktquellen sind es, die dann die Richtung des ausfallenden Strahls bestimmt.
Meine Vermutung ist, dass das, was man in dem Video als die anderen Wellenfronten zu erkennen meint, letztlich eine Art "Aliasingeffekt" ist und dass eine Verletzung des Nyquistkriteriums/Abtasttheorems vorlieft. Normalerweise denkt man beim Abtasttheorem an eine zeitliche Abtastung, aber bei der örtlichen Abtastung, die wir durch die Punktquellen realisieren, gilt ja auch Entsprechendes.
Das trifft m. E. auch für die übliche Erklärung mit dem "Huygens'schen Prinzip" zu. Die Einschränkung, dass man die einlaufenden Wellenfronten "zusammenbehält", ist wohl die Grundlage dafür, dass diese Erklärung trotzdem (nur näherungsweise?) korrekte Winkel vorhersagt.
Die Frage "nur näherungsweise?" stelle ich, da ich mir nicht ganz sicher bin, dass das Snellius'sche Gesetz in der Optik wirklich alle relevanten Effekte, die an der Grenzfläche auftreten, berücksichtigt.
Das "Umbiegen" der E-Feld-Vektoren an der Grenzfläche aufgrund des Brechungsgesetzes für Felder, deutet aus meiner Sicht darauf hin, dass die Huygens'schen Wellen eine Richtcharakteristik aufweisen könnten und somit in manche Richtungen stärker strahlen als in andere. Auch besteht aus meiner Sicht Grund für die Annahme, dass das Reflexionsgesetz bei schmalen Strahlenbündeln und ebenen Wellen möglicherweise anders aussieht, da die Amplitudenverteilung auf der Grenzfläche voneinander abweicht. Über Doppelbrechung, Polarisation, Reflexions- und Transmissionsfaktoren u. ä. haben wir uns in dem Zusammenhang ja auch noch nicht unterhalten.
Viele Grüße
Michael
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 29. Feb 2020 18:42 Titel: index_razor Verfasst am: 29. Feb 2020 18:42 Titel: |
 |
|
| ML hat Folgendes geschrieben: | Hallo,
| index_razor hat Folgendes geschrieben: | Auf jeden Fall sehe ich keinen offensichtlichen Fehler in den Argumenten im Video, die zu den anderen Resultaten führen; zumindest keine, die sich mit dem Huygensschen Prinzip und auf Basis derselben Methoden allein begründen ließen.
|
Ich habe nochmal in das Video reingeschaut und glaube jetzt zu wissen, was da falsch läuft:
Wenn ich das richtig sehe, lässt das Video nur von den Punkten der Grenzfläche Elementarwellen ausgehen, an denen gerade ein Wellenberg ankommt. Die Punktquellen auf der Grenzfläche müssen aber eigentlich kontinuierlich absenden, und zwar von jedem (bestrahlten) Punkt der Oberfläche ausgehend.
|
Das stimmt natürlich. Deswegen ja auch meine Versuche die Eindeutigkeit aus der analytischen Formulierung des Huygensschen Prinzips in Integralform abzulesen.
| Zitat: |
| Zitat: | | Mir ist einfach nicht klar, wie ich von einer einlaufenden monochromatischen Welle auf die Richtung des Ausbreitungsvektors komme, wenn ich nur das Huygenssche Prinzip verwenden darf. |
Die Richtungsinformation über das einfallende Licht steckt letztlich in der Phasendifferenz zwischen den einzelnen Punktquellen: Wenn ein Lichtbündel senkrecht auf eine (sagen wir: plane) Glasfläche einfällt, werden alle Punkte gleichphasig angeregt. Wenn das Licht schräg von rechts einfällt, liegen Phasendifferenzen vor, weil der linke Teil des Lichtbündels eine weitere Strecke durch die Luft laufen muss als der rechte.
Die zugehörigen Phasendifferenzen bei den Punktquellen sind es, die dann die Richtung des ausfallenden Strahls bestimmt.
|
Qualitativ ist mir ungefähr klar, wie es funktionieren soll. Ich habe mich nur gefragt, ob das Kirchhoff-Helmholtz-Integral für gegebenes  der einfallenden Welle und gegebenes der einfallenden Welle und gegebenes  der Elementarwellen immer noch mehrere Lösungen zuläßt, oder ob die scheinbare Mehrdeutigkeit lediglich daher kommt, daß im Video zu grobes Sampling verwendet wird (also nicht mit hinreichend dichter Punktmenge). Ich vermute jetzt eher, daß letzteres der Fall ist. der Elementarwellen immer noch mehrere Lösungen zuläßt, oder ob die scheinbare Mehrdeutigkeit lediglich daher kommt, daß im Video zu grobes Sampling verwendet wird (also nicht mit hinreichend dichter Punktmenge). Ich vermute jetzt eher, daß letzteres der Fall ist.
| Zitat: |
Meine Vermutung ist, dass das, was man in dem Video als die anderen Wellenfronten zu erkennen meint, letztlich eine Art "Aliasingeffekt" ist und dass eine Verletzung des Nyquistkriteriums/Abtasttheorems vorlieft.
|
Das ist eine sehr gute Überlegung. Ich denke damit kommen wir der Sache näher. Klar, dort wird nur in Abständen von  gesamplet (von Wellenberg zu Wellenberg). Das ist natürlich zu wenig. Ich brauche zumindest noch die Information über die Täler. gesamplet (von Wellenberg zu Wellenberg). Das ist natürlich zu wenig. Ich brauche zumindest noch die Information über die Täler.
| Zitat: |
Das trifft m. E. auch für die übliche Erklärung mit dem "Huygens'schen Prinzip" zu. Die Einschränkung, dass man die einlaufenden Wellenfronten "zusammenbehält", ist wohl die Grundlage dafür, dass diese Erklärung trotzdem (nur näherungsweise?) korrekte Winkel vorhersagt.
Die Frage "nur näherungsweise?" stelle ich, da ich mir nicht ganz sicher bin, dass das Snellius'sche Gesetz in der Optik wirklich alle relevanten Effekte, die an der Grenzfläche auftreten, berücksichtigt.
Das "Umbiegen" der E-Feld-Vektoren an der Grenzfläche aufgrund des Brechungsgesetzes für Felder, deutet aus meiner Sicht darauf hin, dass die Huygens'schen Wellen eine Richtcharakteristik aufweisen könnten und somit in manche Richtungen stärker strahlen als in andere.
|
Also das Umbiegen folgt doch auch aus den Maxwellgleichungen ganz ohne Huygenssches Prinzip. In welcher Form das Huygenssche Prinzip in der Situation, in der das Brechungsgesetz normalerweise abgeleitet wird, anwendbar ist, würde ich auch gern wissen. Da das komplette Problem nicht mehr isotrop ist, kann ich mir auch gut vorstellen, daß das für die Elementarwellen nicht mehr gilt. Wahrscheinlich wird man mit dem üblichen Ansatz nur für Punkte in ausreichender Entfernung von der Grenzfläche zuverlässige Aussagen bekommen, da in der Nähe der Grenzfläche ja c einen Sprung macht, die Gültigkeit der Wellengleichung also aussetzt. Damit sind auch die Voraussetzungen des Huygenschen Prinzips hinfällig, so wie ich es verstehe.
| Zitat: |
Auch besteht aus meiner Sicht Grund für die Annahme, dass das Reflexionsgesetz bei schmalen Strahlenbündeln und ebenen Wellen möglicherweise anders aussieht, da die Amplitudenverteilung auf der Grenzfläche voneinander abweicht. Über Doppelbrechung, Polarisation, Reflexions- und Transmissionsfaktoren u. ä. haben wir uns in dem Zusammenhang ja auch noch nicht unterhalten.
|
Hm, das wäre wahrscheinlich noch eine ganz neue Diskussion. Ich würde erstmal gern einen möglichst einfachen Fall verstehen.
|
|
 |
|
|















