| Autor |
Nachricht |
physikstudent0815
Gast
|
 physikstudent0815 Verfasst am: 06. Aug 2019 21:34 Titel: Variationsrechnung Lagrangefunktion physikstudent0815 Verfasst am: 06. Aug 2019 21:34 Titel: Variationsrechnung Lagrangefunktion |
 |
|
Meine Frage:
Hallo,
bei der Variationsrechnung habe ich Probleme und würde mich freuen, wenn mir da jemand auf die Sprünge helfen könnte. Danke :)
Gesucht ist die Variation von 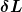 in Abhängigkeit von in Abhängigkeit von  bei einer infinitisimalen Verschiebung bei einer infinitisimalen Verschiebung  \rightarrow q(t) + \epsilon)
Meine Ideen:
Ich lasse aus Übersichtsgründen ab sofort die  Abhängigkeiten weg, was nicht heißt, dass dem nicht so ist, sprich Abhängigkeiten weg, was nicht heißt, dass dem nicht so ist, sprich
, \dot{q}=\dot{q}(t) )
 - L(q,\dot{q},t) )
(ist das so richtig oder ist hier schon der Fehler?)
Dann betrachte ich die Taylorentwicklung in  von von
 )
Allgemein gilt:
 \approx \left(f(x)\right)_{x=0} + \left( \frac{\partial f(x)}{\partial x}\right)_{x=0} \cdot x + O(x^{2}) )
Also gilt hier im Entwicklungspunkt 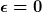
 \approx L(q,\dot{q},t) + \frac{\partial L(q+\epsilon,\dot{q},t)}{\partial (q+\epsilon)}\cdot \epsilon + O(\epsilon ^{2}) )
Mir ist nun nicht klar, warum gelten soll:
}{\partial (q+\epsilon)} = \frac{\partial L(q,\dot{q},t)}{\partial q} )
Laut Lösung muss das so sein, denn die ist gegeben mit

Man darf ja nun nicht einfach  Null setzen, da ja nach einem Ausdruck Null setzen, da ja nach einem Ausdruck  abgeleitet wird oder doch? abgeleitet wird oder doch?
Wäre sehr dankbar, wenn mir hier jemand weiterhelfen könnte  |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 06. Aug 2019 23:15 Titel: franz Verfasst am: 06. Aug 2019 23:15 Titel: |
 |
|
Mir ist das Konzept rätselhaft: Die Lagrangegleichung ergibt sich aus dem Wirkungsprinzip (Hamilton)  ; zu integrieren zwischen zwei Punkten usw. (siehe vielleicht Landau / Lifschitz I §2). ; zu integrieren zwischen zwei Punkten usw. (siehe vielleicht Landau / Lifschitz I §2). |
|
 |
physikstudent0815
Gast
|
 physikstudent0815 Verfasst am: 07. Aug 2019 10:06 Titel: physikstudent0815 Verfasst am: 07. Aug 2019 10:06 Titel: |
 |
|
Es geht hier nicht um die Herleitung der Euler Lagrange Gleichung sondern schlussendlich um die Impulserhaltung aus dem Lagrangeformalismus. Man sagt dann, wegen der Homogenität des Raumes muss 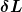 Null sein und da Epsilon beliebig ist, muss also Null sein und da Epsilon beliebig ist, muss also  Null sein. Null sein.
Ich verstehe nur die Taylorentwicklung bzw. das Epsilon = 0 setzen hier nicht und warum das in dem Operator gemacht werden darf |
|
 |
Gast002
Gast
|
 Gast002 Verfasst am: 07. Aug 2019 17:30 Titel: Gast002 Verfasst am: 07. Aug 2019 17:30 Titel: |
 |
|
Hallo Physikstudent0815,
es ist besser, Du setzt die Taylorentwicklung nicht um den Argumentwert x = 0 an, sondern um eine beliebige Stelle x0:
 \approx f(x_0) + (\frac{\partial f(x)}{\partial x} )_{x=x_0} * \Delta x + O({\Delta x}^2)) . .
Auf die Lagrangefunktion bezogen entwickelst Du also um die Stelle q.
Beste Grüße |
|
 |
physikstudent0815
Gast
|
 physikstudent0815 Verfasst am: 07. Aug 2019 18:31 Titel: physikstudent0815 Verfasst am: 07. Aug 2019 18:31 Titel: |
 |
|
Hallo Gast002,
dann würde die Entwicklung der Funktion
 )
um die Stelle 
doch folgenermaßen aussehen:
 \approx L(q+q, \dot{q}, t) + \left(\frac{\dd L(q+\epsilon, \dot{q}, t)}{\dd \epsilon}\right)_{\epsilon=q} \cdot (\epsilon - q) + O((\epsilon - q)^{2}) )
Sieht für mich noch nicht richtig aus und soweit ich das verstanden habe Entwickelt man schon nach 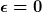 . Zumindest passiert es bei der Herleitung der Invarianzbedingung beim Noethertheorem genauso (sieht z.B. Fließbach Mechanik das entsprechende Kapitel). Das vorgehen ist hier logischerweise ganz analog. . Zumindest passiert es bei der Herleitung der Invarianzbedingung beim Noethertheorem genauso (sieht z.B. Fließbach Mechanik das entsprechende Kapitel). Das vorgehen ist hier logischerweise ganz analog.
Mir ist nicht klar, um es vielleicht nochmal genauer auf den Punkt zu bringen, warum z.B.
}{\dd \epsilon} \right]_{\epsilon=0})
also diese Ableitung ausgewertet an der Stelle 
folgendes ergibt:
}{\partial q}\cdot a)
Ich komme in meiner Rechnung so weit:
}{\dd \epsilon} \right]_{\epsilon=0} =)
}{\partial (q+a\epsilon)} \frac{\dd (q+a\epsilon)}{\dd \epsilon}\right]_{\epsilon=0} = )
}{\partial (q+a\epsilon)}\cdot a\right]_{\epsilon=0} )
Warum darf ich hier nun anscheinend  setzen? setzen?
Die Auswertung an dieser Stelle ist doch erst nach der Ableitung von ) nach nach  vorzunehmen. vorzunehmen.
Es macht ja z.B. einen Unterschied ob ich die Funktion =x^{2}) vor oder nach dem Ableiten an der Stelle vor oder nach dem Ableiten an der Stelle  auswerte. Einmal ist das Ergebnis hier 1 und einmal 2... auswerte. Einmal ist das Ergebnis hier 1 und einmal 2...
Da ich das Argument von 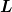 nicht genauer kenne sondern nur weis, dass nicht genauer kenne sondern nur weis, dass 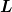 in irgendeiner Weise von in irgendeiner Weise von  abhängt weiß ich nicht wie man eben auf die oben genannte Löung kommt, ohne hier gleich abhängt weiß ich nicht wie man eben auf die oben genannte Löung kommt, ohne hier gleich  im Argument und im Operator zu setzen, was für mich mathematisch aus oben genannter Argumentation nicht richtig zu sein scheint.... im Argument und im Operator zu setzen, was für mich mathematisch aus oben genannter Argumentation nicht richtig zu sein scheint....
Liebe Grüße |
|
 |
Gast002
Gast
|
 Gast002 Verfasst am: 07. Aug 2019 18:47 Titel: Gast002 Verfasst am: 07. Aug 2019 18:47 Titel: |
 |
|
Hallo,
das hast Du leider falsch verstanden. Das 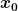 bedeutet eine fest vorgegebene Stelle im Definitionsbereich der Funktion, in deren Umgebung die Funktion näherungsweise dargestellt werden soll. Das bedeutet eine fest vorgegebene Stelle im Definitionsbereich der Funktion, in deren Umgebung die Funktion näherungsweise dargestellt werden soll. Das 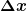 ist die kleine Differenz des aktuellen Arguments zu dieser vorgegebenen Stelle. ist die kleine Differenz des aktuellen Arguments zu dieser vorgegebenen Stelle.
Auf die Lagrangefunktion bezogen entspricht das q dem 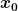 und das und das  dem dem 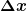 . Das ist auch sinnvoll im Hinblick darauf, daß das . Das ist auch sinnvoll im Hinblick darauf, daß das  ja eine kleine Variation sein soll. ja eine kleine Variation sein soll.
Beste Grüße |
|
 |
physikstudent0815
Gast
|
 physikstudent0815 Verfasst am: 07. Aug 2019 19:07 Titel: physikstudent0815 Verfasst am: 07. Aug 2019 19:07 Titel: |
 |
|
Hallo,
vielen Dank für die Antworten erstmal 
Ich denke ich hab so ziemlich viel falsch bzw. nicht verstanden, leider -.-
Okey dann zurück zum Thema:
Wenn hier also  und und  ist, dann fehlt immer noch ist, dann fehlt immer noch  um die oben gegebene Formel der Taylorentwicklung anweden zu können. Dort kommt ja der Ausdruck um die oben gegebene Formel der Taylorentwicklung anweden zu können. Dort kommt ja der Ausdruck
}{\partial x} ) vor... vor...
Was wäre dann denn  in meinem Fall? in meinem Fall?
Liebe Grüße |
|
 |
Gast002
Gast
|
 Gast002 Verfasst am: 07. Aug 2019 21:27 Titel: Gast002 Verfasst am: 07. Aug 2019 21:27 Titel: |
 |
|
Hallo,
in der Schreibweise der Taylorentwicklung für die Lagrangefunktion ist die Schreibweise nicht ganz sauber (aber in der Physik üblich). Das q wird in zwei verschiedenen Bedeutungen verwendet - zum einen für die Stelle, um die entwickelt werden soll, und zum anderen als erstes Argument der Lagrangefunktion bei der Berechnung der partiellen Ableitung (ohne einen Wert für q vorzugeben).
Wenn ich es mathematisch sauber schreiben will, muß ich für das Argument bei der Ableitung eine andere Variable benutzen, z. B.  . Die Entwicklung der Lagrangefunktion lautet dann: . Die Entwicklung der Lagrangefunktion lautet dann:
 \approx L(q, \dot {q}, t) + (\frac {\partial L(\tilde {q}, \dot {q}, t)}{\partial {\tilde {q}}})_{\tilde {q} = q} * \epsilon + O(\epsilon^2)
<br />
)
Beste Grüße |
|
 |
physikstudent0815
Gast
|
 physikstudent0815 Verfasst am: 08. Aug 2019 13:08 Titel: physikstudent0815 Verfasst am: 08. Aug 2019 13:08 Titel: |
 |
|
Hallo,
vielen Dank für die Antwort. Da ich es wirklich gerne verstehen würde, muss ich aber nochmal nachfragen. Mir ist schon öfter die schlapsige Schreibweise in der Physik zum Verhängnis geworden, aber wenn ich es mal sauber und ausführlich für mich aufgeschrieben habe passt es meistens dann auch in der laissez-fairen Art für mich 
So, nun nochmal von vorne, da ich mir nicht sicher bin, ob wir nicht aneinander vorbei reden. Mein Problem denke ich, ist hier nicht in erster Linie die Taylorentwicklung sondern die Auswertung von einem Ausdruck der Form:
 \right]_{\epsilon=0})
So ist er z.B. im Fließbach Mechanik zu finden. Ich habe hier nur die 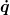 und und  Abhängigkeiten von Abhängigkeiten von 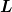 aus Übersichtsgründen weggelassen, das Vorgehen hier ist ja dann analog. aus Übersichtsgründen weggelassen, das Vorgehen hier ist ja dann analog.
Auch aus Übersichtsgründen fehlt  )
So, gehen wir nun von diesem Ausdruck aus. Auf den komme ich und die Taylorentwicklung dazu ist bereits einige Schritte zuvor passiert. Die weitere Auswertung hat doch nichts mehr mit einer Taylorentwichlung zu tun oder etwa doch?
Meiner Meinung nach muss hier jetzt nach Epsilon abgeleitet werden und dann an der stelle 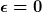 ausgewertet werden. ausgewertet werden.
Die nächste Zeile im Buch ist also:

Meine Frage: Wie kommt man von der Gleichung oben ausgehend darauf?
Ich würde wie gesagt so vorgehen:
 \right]_{\epsilon=0})
-> Kettenregel
} \cdot \frac{\dd (q+\epsilon \psi)}{\dd \epsilon} \right]_{\epsilon=0})
-> Der zweite Ausdruck im Produkt lässt sich weiter auswerten:
}{\dd \epsilon} = \psi)
Also steht nun da:
} \cdot \frac{\dd (q+\epsilon \psi)}{\dd \epsilon} \right]_{\epsilon=0} = )
} \cdot \psi \right]_{\epsilon=0})
Ein Vergleich mit der oben genannten nächsten Zeile im Buch zeigt mir also dass
} \right]_{\epsilon=0})
gelten muss. Aber warum? Im Buch steht auch: "Der Index Epsilon = 0 bedeutet, dass die nach Epsilon differenzierte Funktion an dieser Stelle zu nehmen ist."
Das entspricht genau meiner Überlegung, dass ich erst ableiten muss und dann Epsilon = 0 setzen (sieher vorheriger Post).
Allerdings weiß ich auch nicht wie der Ableitung ausgeführt werden kann da ich die konketen Funktionen ja nicht kenne.
Wo ist mein Fehler, bzw. wie geht es also weiter?
Erkenne ich hier wirklich eine nochmalige Taylorentwicklung nicht?
Sry, dass ich so aufdringlich nachfrage, aber ich würde es wirklich gerne verstehen und Danke nochmal für die Antworten.
Liebe Grüße |
|
 |
|
















