| Autor |
Nachricht |
Sito
Anmeldungsdatum: 14.07.2017
Beiträge: 31
|
 Sito Verfasst am: 30. Okt 2017 22:49 Titel: Trägheitstensor Sito Verfasst am: 30. Okt 2017 22:49 Titel: Trägheitstensor |
 |
|
Meine Frage:
Guten Abend zusammen,
Folgende Aufgabestellung bereitet mir etwas Kopfzerbrechen:
Wir betrachten ein Ellipsoid mit Hauptachsen  . Es hat eine gleichmässige Massendichte . Es hat eine gleichmässige Massendichte 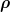 und Gesamtmasse und Gesamtmasse 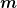 und rotiert frei im einem Inertialensystem. und rotiert frei im einem Inertialensystem.
Die Aufgabe ist es nun den Trägheitstensor zu bestimmen.
Meine Ideen:
Um ehrlich zu sein habe ich in der Vorlesung überhaupt nicht verstanden was dieser Tensor genau sein soll, bzw. für was er gut ist... Daraufhin habe ich mich versucht in den Bücher Theoretische Physik von M. Bartelmann und Klassische Mechanik 1 von W. Nolting schlau zu machen, aber leider habe ich die Erklärungen dort auch nicht wirklich verstanden...
Die erste Frage wäre also, kann mir jemand erklären um was es sich bei diesem Tensor handelt und wo der Unterschied/Vorteil zum "gewöhnlichen" Trägheitsmoment ist.
Die zweite Frage ist nun konkret auf die Aufgabe bezogen.. Kann mir jemand erklären wie man in diesem Fall den Tensor berechnet... Wikipedia hat zwar diverse Formeln, wie z.B. \pmb{1}-\vec{x}_i \otimes \vec{x}_i ]) , usw., aber da blicke ich leider überhaupt nicht durch... , usw., aber da blicke ich leider überhaupt nicht durch...
Gruss Sito |
|
 |
Tensortensortensor
Gast
|
 Tensortensortensor Verfasst am: 30. Okt 2017 22:59 Titel: Tensortensortensor Verfasst am: 30. Okt 2017 22:59 Titel: |
 |
|
Vielleicht ist Studium doch nicht das Richtige?
Ein Student sollte mindestens herausfinden können was in der Aufgabe verlangt ist. Was ist denn nun ein Trägheitstensor?! Würde mich auch interessieren. |
|
 |
Sito
Anmeldungsdatum: 14.07.2017
Beiträge: 31
|
 Sito Verfasst am: 30. Okt 2017 23:40 Titel: Sito Verfasst am: 30. Okt 2017 23:40 Titel: |
 |
|
| Zitat: | | Was ist denn nun ein Trägheitstensor?! |
Wenn ich das erklären könnte würde ich hier nicht fragen... Mir ist schon klar, dass der Trägheitstensor die Verallgemeinerung zum Trägheitsmoment darstellt. Es heisst zwar, dass das Trägheitsmoment von der Drehachse abhängt, aber wieso kann ich mir nur mathematisch erklären, intuitiv aber gar nicht.
Wieso gibt zum Bsp. der Trägheitstensor die Körperträgheit an, wenn man irgendwelche Drehungen durch den Körperschwerpunkt betrachtet? (Bin mir nicht mal sicher was Drehung durch den Körperursprung bedeutet, Drehung mit einem Fixpunkt im Schwerpunkt?)
Zudem ist mir der Begriff Tensor ziemlich fremd, bzw. ich habe noch überhaupt keine Erfahrung mit Tensoren, kenne also auch nicht wirklich Eigenschaften davon.. Und um das gleich auch zu sagen, ja ich habe mich versucht darüber schlau zu machen, bzw. meine Vorlesungsnotizen danach durchsucht, aber die Einführung in die Multilineare Algebra die wir hatten war ziemlich dünn..
Insofern weiss ich also sehr wohl was meine Aufgabe ist, aber ich weiss nicht wie ich sie angehen soll. |
|
 |
Tensorallgemein
Gast
|
 Tensorallgemein Verfasst am: 30. Okt 2017 23:57 Titel: Tensorallgemein Verfasst am: 30. Okt 2017 23:57 Titel: |
 |
|
Du klingst ganz schön verwirrt. Vielleicht hilft es dir noch mal bei Wikipedia nachzuschlagen 
Oder du lässt das Studium sausen wie 90% deiner mitstudis und gehst erstmal schön feiern. 
Facharbeiter wie Maler, Bäcker oder Maurer sollen im Moment schwer gefragt sein.   |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8583
|
 jh8979 Verfasst am: 31. Okt 2017 01:54 Titel: jh8979 Verfasst am: 31. Okt 2017 01:54 Titel: |
 |
|
Als Moderator würde ich um einen etwas netter Tonfall dem Fragesteller gegenüber bitten. Es ist nicht so, dass seine Frage so trivial und dumm wäre, wie dargestellt...
Zur Frage:
Schau mal hier. Da ist recht einfach beschrieben, wie man auf den Tensor kommt.
http://www.ieap.uni-kiel.de/et/download/physik1/V6.pdf
Hoffe es hilft. |
|
 |
Tensortrivial
Gast
|
 Tensortrivial Verfasst am: 31. Okt 2017 10:10 Titel: Tensortrivial Verfasst am: 31. Okt 2017 10:10 Titel: |
 |
|
Na klar lebt die Moderation von den Fragestellern. Hier kann nichts trivial genug sein. 
Kann ich dann auch eine Frage stellen:
Also wir haben vom Professor die Hausaufgabe bekommen heraus zu finden was denn nun ein Tensor ist. Das nannte man früher auch Studium. Die Hochschulbibliothek ist voll mit Büchern?! Leider kann er den Duden nicht finden. Hat schon ein Austauschstudent ausgeliehen. Und das Abitur war sowieso schon so schwer für ihn. Was machen wir denn nun? Physikerboard ist SEINE letzte Hoffnung bevor er das Studium abbricht! Also hilf ihm lieber Moderator!!! Bitte bitte so hilf ihm doch! Seine Hoffnungen schwinden bereits. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8583
|
 jh8979 Verfasst am: 31. Okt 2017 11:13 Titel: jh8979 Verfasst am: 31. Okt 2017 11:13 Titel: |
 |
|
|
Versteh ehrlich gesagt nicht was diese Polemik soll. Nach Deiner Logik kann man gleich ganz aufhören andere zu fragen, weil ja eh alles irgendwo steht. Die Frage hier war vllt nicht besonders schwer, aber nicht unangemessen. |
|
 |
DemTensöristeszuschwör
Gast
|
 DemTensöristeszuschwör Verfasst am: 31. Okt 2017 12:26 Titel: DemTensöristeszuschwör Verfasst am: 31. Okt 2017 12:26 Titel: |
 |
|
| jh8979 hat Folgendes geschrieben: | | Versteh ehrlich gesagt nicht was diese Polemik soll. Nach Deiner Logik kann man gleich ganz aufhören andere zu fragen, weil ja eh alles irgendwo steht. Die Frage hier war vllt nicht besonders schwer, aber nicht unangemessen. |
Dann beantworte doch seine Frage wenn sie nicht so schwer ist. Meine Aufregung begründet sich darauf, dass es seine Hausaufgabe ist den Sachverhalt des Tensors zu ergründen. Er macht es sich jedoch ganz einfach und fragt hier herum. So hat et wohl auch das Abitur geschafft. Selber lernen ist zu anstrengend.
Meiner Meinung nach ist er in der Pommesbude besser aufgehoben als im Hörsaal die Atemluft des Profs zu verbrauchen. In diesem Jahr studiert wieder eine Rekordzahl an Nullen, weil das allgemeine Abitur anscheinend viel zu leicht geworden ist. Wenn man nix konnte ging man früher als Hiwi auf die Baustelle. Heute gehen nix könner einfach mal studieren und japsen oftmals 10 Semester herum bis der Prof. Mitleid hat und sie endlich nach Hause schickt. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8583
|
 jh8979 Verfasst am: 31. Okt 2017 12:31 Titel: jh8979 Verfasst am: 31. Okt 2017 12:31 Titel: |
 |
|
|
Die ständigen, ungerechtfertigten Beleidigungen verkneifst Du Dir bitte ab sofort. Mir reicht es. Dies ist nicht der Ton, den wir hier pflegen. |
|
 |
Tensorzuschwer
Gast
|
 Tensorzuschwer Verfasst am: 31. Okt 2017 12:38 Titel: Tensorzuschwer Verfasst am: 31. Okt 2017 12:38 Titel: |
 |
|
Gib doch einfach zu, dass euch seine Frage zu viel Mühe und Arbeit kostet und ihr lieber um den heißen Brei redet von wegen Netiquette und so.
[jh8979: Unangemessenes gelöscht] |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8583
|
 jh8979 Verfasst am: 31. Okt 2017 12:43 Titel: jh8979 Verfasst am: 31. Okt 2017 12:43 Titel: |
 |
|
| Tensorzuschwer hat Folgendes geschrieben: | Gib doch einfach zu, dass euch seine Frage zu viel Mühe und Arbeit kostet und ihr lieber um den heißen Brei redet von wegen Netiquette und so.
|
Hab ihm doch geantwortet und gezeigt, wo er fündig werden kann.
Stichwort: Hilfe zur Selbsthilfe.
https://www.physikerboard.de/ueberuns.php
Wenn er dann immer noch nicht weiter kommt und/oder weitere Fragen hat, kann er die ja gerne stellen. |
|
 |
Sito
Anmeldungsdatum: 14.07.2017
Beiträge: 31
|
 Sito Verfasst am: 31. Okt 2017 23:01 Titel: Sito Verfasst am: 31. Okt 2017 23:01 Titel: |
 |
|
Zuerst einmal vielen Dank an dich jh8979, sowohl für den Link als auch für das Moderieren.
Nach dem Durchlesen hätte ich aber doch noch ein, zwei Fragen: Ich kann nachvollziehen wieso  gilt. Mit was ich aber immer noch Mühe habe ist gilt. Mit was ich aber immer noch Mühe habe ist ) . In dieser Gleichung stellen . In dieser Gleichung stellen  die einzelnen Komponenten die einzelnen Komponenten  des Punktes des Punktes 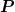 dar, oder? In diesem Fall sind also die einzelnen Komponenten des Tensors eine Summe aus der Multiplikation der einzelnen Massen des starren Körpers mit dem geklammerten Ausdruck. Wenn ich nun, wie z.B. in der von mir im ersten Beitrag geschilderten Situation, eine kontinuierliche Dichte über ein Volumen habe, was passiert dann mit den Einträgen? Habe ich dann etwas von der Form dar, oder? In diesem Fall sind also die einzelnen Komponenten des Tensors eine Summe aus der Multiplikation der einzelnen Massen des starren Körpers mit dem geklammerten Ausdruck. Wenn ich nun, wie z.B. in der von mir im ersten Beitrag geschilderten Situation, eine kontinuierliche Dichte über ein Volumen habe, was passiert dann mit den Einträgen? Habe ich dann etwas von der Form {\rm{d}}V) ? Und ist dies der Link zu den auf Seite 6 & 7 aufgezeichneten Komponenten? (Es wäre auch schön, wenn mir hier nochmal jemand bestätigen könnte, dass es sich bei dem ? Und ist dies der Link zu den auf Seite 6 & 7 aufgezeichneten Komponenten? (Es wäre auch schön, wenn mir hier nochmal jemand bestätigen könnte, dass es sich bei dem 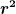 um um  handelt (anders kann ich mir zumindest die Einträge dort nicht erklären)).. handelt (anders kann ich mir zumindest die Einträge dort nicht erklären))..
Die nächste Frage wäre bzgl. der Aussagen auf Seite 10. Bis und mit "Wir berechnen für eine Rotation um eine beliebige Achse  durch einen Punkt durch einen Punkt 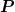 das Trägheitsmoment das Trägheitsmoment  " konnte ich soweit folgen, aber was sie dann zum Trägheitsellipsoiden bzw. den Hauptträgheitsachsen sagen verstehe ich leider nicht. " konnte ich soweit folgen, aber was sie dann zum Trägheitsellipsoiden bzw. den Hauptträgheitsachsen sagen verstehe ich leider nicht.
Abschliessend noch eine Frage zur Notation, da ich zum ersten mal mit der Einsteinschen Summenkonvention konfrontiert wurde: =\sum_{l=1}^{3}\sum_{j=1}^3\sum_{k=1}^3(r_l^2\delta_{jk}-r_jr_k)) , insbesondere zählt hier , insbesondere zählt hier  auch als doppelt vorkommender Index, oder? auch als doppelt vorkommender Index, oder?
Danke schon mal im Vorraus.
Gruss Sito |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8583
|
 jh8979 Verfasst am: 31. Okt 2017 23:15 Titel: jh8979 Verfasst am: 31. Okt 2017 23:15 Titel: |
 |
|
| Sito hat Folgendes geschrieben: |
Nach dem Durchlesen hätte ich aber doch noch ein, zwei Fragen: Ich kann nachvollziehen wieso  gilt. Mit was ich aber immer noch Mühe habe ist gilt. Mit was ich aber immer noch Mühe habe ist ) . In dieser Gleichung stellen . In dieser Gleichung stellen  die einzelnen Komponenten die einzelnen Komponenten  des Punktes des Punktes 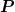 dar, oder? In diesem Fall sind also die einzelnen Komponenten des Tensors eine Summe aus der Multiplikation der einzelnen Massen des starren Körpers mit dem geklammerten Ausdruck. Wenn ich nun, wie z.B. in der von mir im ersten Beitrag geschilderten Situation, eine kontinuierliche Dichte über ein Volumen habe, was passiert dann mit den Einträgen? Habe ich dann etwas von der Form dar, oder? In diesem Fall sind also die einzelnen Komponenten des Tensors eine Summe aus der Multiplikation der einzelnen Massen des starren Körpers mit dem geklammerten Ausdruck. Wenn ich nun, wie z.B. in der von mir im ersten Beitrag geschilderten Situation, eine kontinuierliche Dichte über ein Volumen habe, was passiert dann mit den Einträgen? Habe ich dann etwas von der Form {\rm{d}}V) ? Und ist dies der Link zu den auf Seite 6 & 7 aufgezeichneten Komponenten? (Es wäre auch schön, wenn mir hier nochmal jemand bestätigen könnte, dass es sich bei dem ? Und ist dies der Link zu den auf Seite 6 & 7 aufgezeichneten Komponenten? (Es wäre auch schön, wenn mir hier nochmal jemand bestätigen könnte, dass es sich bei dem 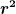 um um  handelt (anders kann ich mir zumindest die Einträge dort nicht erklären)).. handelt (anders kann ich mir zumindest die Einträge dort nicht erklären))..
|
Deine Überlegungen sind richtig.
| Zitat: |
Die nächste Frage wäre bzgl. der Aussagen auf Seite 10. Bis und mit "Wir berechnen für eine Rotation um eine beliebige Achse  durch einen Punkt durch einen Punkt 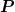 das Trägheitsmoment das Trägheitsmoment  " konnte ich soweit folgen, aber was sie dann zum Trägheitsellipsoiden bzw. den Hauptträgheitsachsen sagen verstehe ich leider nicht. " konnte ich soweit folgen, aber was sie dann zum Trägheitsellipsoiden bzw. den Hauptträgheitsachsen sagen verstehe ich leider nicht.
|
Ist auch nicht so schön beschreiben, wenn man nicht schon weiss was sie meinen.
Hier steht es etwas ausführlicher (und vor allem mit einem Bild):
https://lp.uni-goettingen.de/get/text/5227
| Zitat: |
Abschliessend noch eine Frage zur Notation, da ich zum ersten mal mit der Einsteinschen Summenkonvention konfrontiert wurde: =\sum_{l=1}^{3}\sum_{j=1}^3\sum_{k=1}^3(r_l^2\delta_{jk}-r_jr_k)) , insbesondere zählt hier , insbesondere zählt hier  auch als doppelt vorkommender Index, oder? auch als doppelt vorkommender Index, oder?
|
l ja, j und k aber nicht. Es geht darum ob ein Index doppelt in einem Summanden auftaucht:

l tritt doppelt auf in diesem Term. j und k aber nur einmal. Es wird also nur über l summiert. |
|
 |
Sito
Anmeldungsdatum: 14.07.2017
Beiträge: 31
|
 Sito Verfasst am: 02. Nov 2017 20:56 Titel: Sito Verfasst am: 02. Nov 2017 20:56 Titel: |
 |
|
Vielen Dank für den zweiten Link, das hat Einiges etwas klarer gemacht.
Nun ein paar konkrete Fragen zur Aufgabenstellung aus dem ersten Beitrag:
Es heisst man solle den Trägheitstensor berechnen, benutzen möchte ich dazu {\rm{d}}V) . Für . Für  erhalte ich das Integral erhalte ich das Integral {\rm{d}}V=\rho\int_V (y^2+z^2){\rm{d}}V) . Nun müsste man also über das Volumen des Ellipsoiden integrieren. . Nun müsste man also über das Volumen des Ellipsoiden integrieren.
Meine Idee war jetzt einen Diffeomorphismus der Form  \mapsto (ar\sin\psi\cos\varphi,ar\sin\psi\sin\varphi,cr\cos\psi)) . Die Jakobi-Determinante wäre in diesem Fall dann: . Die Jakobi-Determinante wäre in diesem Fall dann:  . Damit könnte man dann zu folgender Gleichung kommen: . Damit könnte man dann zu folgender Gleichung kommen:
a^2r^2c\sin\psi {\rm{d}}\varphi {\rm{d}} \psi {\rm{d}}r = \frac{4}{15}a^2(a^2+c^2)\pi\rho)
Ich könnte natürlich noch vier weitere solche Integrale ausrechnen, aber die Frage stellt sich langsam, ob es nicht vlt. eine etwas elegantere Methode gibt das Problem zu lösen... |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8583
|
 jh8979 Verfasst am: 02. Nov 2017 20:58 Titel: jh8979 Verfasst am: 02. Nov 2017 20:58 Titel: |
 |
|
| Sito hat Folgendes geschrieben: | Nun müsste man also über das Volumen des Ellipsoiden integrieren.
|
Nein, Du musst natürlich über das Volumen des zu betrachtenden Körpers integrieren. Der muss ja kein Ellipsoid sein. |
|
 |
Sito
Anmeldungsdatum: 14.07.2017
Beiträge: 31
|
 Sito Verfasst am: 02. Nov 2017 21:24 Titel: Sito Verfasst am: 02. Nov 2017 21:24 Titel: |
 |
|
Aber ist nicht das genau die Aufgabe wenn es heisst:
| Zitat: | Wir betrachten ein Ellipsoid mit Hauptachsen  . Es hat eine gleichmässige Massendichte . Es hat eine gleichmässige Massendichte 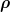 und Gesamtmasse und Gesamtmasse 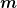 und rotiert frei im einem Inertialensystem. und rotiert frei im einem Inertialensystem. |
 |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8583
|
 jh8979 Verfasst am: 02. Nov 2017 21:30 Titel: jh8979 Verfasst am: 02. Nov 2017 21:30 Titel: |
 |
|
| Sito hat Folgendes geschrieben: | Aber ist nicht das genau die Aufgabe wenn es heisst:
| Zitat: | Wir betrachten ein Ellipsoid mit Hauptachsen  . Es hat eine gleichmässige Massendichte . Es hat eine gleichmässige Massendichte 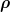 und Gesamtmasse und Gesamtmasse 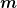 und rotiert frei im einem Inertialensystem. und rotiert frei im einem Inertialensystem. |
 |
Ach so, ja klar, dann schon. Ich dachte Du hättest noch den Trägheitsellipsoiden im Kopf. |
|
 |
Sito
Anmeldungsdatum: 14.07.2017
Beiträge: 31
|
 Sito Verfasst am: 03. Nov 2017 17:51 Titel: Sito Verfasst am: 03. Nov 2017 17:51 Titel: |
 |
|
Das mit dem berechnen des Tensors hat soweit geklappt. Die nächste Frage hat zwar nichts mit der eigentlichen Aufgabe zu tun, aber es beschäftigt mich doch ein wenig...
Auf der Seite https://lp.uni-goettingen.de/get/text/5227 wird anhand eines Bsp. erklärt wieso es sinnvoll ist den Trägheitselipsoiden für einen starren Körper zu bestimmen. Dort heisst es, dass für eine beliebige Drehachse  , dass Trägheitsmoment durch , dass Trägheitsmoment durch  gegeben ist. Daraus folgern sie dann, dass also der Vektor gegeben ist. Daraus folgern sie dann, dass also der Vektor  den Trägheitselipsoiden im Punkt den Trägheitselipsoiden im Punkt  schneidet. schneidet.
Was mich jetzt aber etwas verwirrt, möchte man nicht in der Regel das Trägheitsmoment herausfinden in dem man 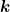 kennt? In diesem Fall müsste man also den Ursprungsabstand von kennt? In diesem Fall müsste man also den Ursprungsabstand von  zur Ellipsoidenoberfläche kennen. Dafür müsste man aber die Gleichung zur Ellipsoidenoberfläche kennen. Dafür müsste man aber die Gleichung  lösen, aber ich verstehe nicht wie man das im Allgemeinen machen soll (immerhin ist a priori nicht klar, bei welchem Punkt lösen, aber ich verstehe nicht wie man das im Allgemeinen machen soll (immerhin ist a priori nicht klar, bei welchem Punkt  den Ellipsoiden schneidet). den Ellipsoiden schneidet). |
|
 |
|



















