| Autor |
Nachricht |
Leoniii
Gast
|
 Leoniii Verfasst am: 28. Nov 2013 22:29 Titel: Trägheitstensor 3D Leoniii Verfasst am: 28. Nov 2013 22:29 Titel: Trägheitstensor 3D |
 |
|
Meine Frage:
Einen guten Abend wünsche ich allen Internauten.
Ich habe den Trägheitstensor 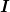 im Koordinatensystem im Koordinatensystem 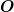 gegeben: gegeben:

a) Berechnen Sie die Trägheitsmomente der Haupträgheitsachsen.
b) Berechnen Sie die Haupträgheitsachsen im Koordinatensystem 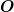
c) Ermitteln Sie, um welche Haupträgheitsachse eine Rotation instabil wäre.
d) Die Winkelgeschwindigkeit sei ) mit mit 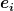 den Einheitsvektoren im Koordinatensystem den Einheitsvektoren im Koordinatensystem 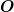 . Bestimmen Sie, in welche Richtung der Drehimpuls zeigt, und für welche Winkelgeschwindigkeitsvektoren . Bestimmen Sie, in welche Richtung der Drehimpuls zeigt, und für welche Winkelgeschwindigkeitsvektoren  parallel zum Drehimpuls ist. parallel zum Drehimpuls ist.
Meine Ideen:
Ich habe noch nicht das physikalische Verständnis dafür, aber die mathematischen Methoden müssten halbwegs sitzen. Ich muss auf jeden Fall die Matrix diagonalisieren, richtig? Und danach bestimme ich Eigenwerte und Eigenvektoren, oder? Nur zur welchem Aufgabenteil ist das? Mir fehlt der physikalische Bezug.
Wenn mir jemand einen kurzen Überblick geben könnte, was zu tun ist, wäre ich demjenigen sehr dankbar zumal ich Aufgaben dieser Art zum ersten Mal erledige.
MfG Leoni |
|
 |
Namenloser324
Gast
|
 Namenloser324 Verfasst am: 28. Nov 2013 23:24 Titel: Namenloser324 Verfasst am: 28. Nov 2013 23:24 Titel: |
 |
|
Ist schon ein wenig her bei mir, daher ohne Gewähr:
a)
Du musst die Eigenwerte von I bestimmen.
Diese sind die Diagonalelemente des Trägheitstensors bezüglich der Hauptträgheitsachsen.
b) Die Eigenvektorenzu den Eigenwerten sind die besagten Achsen
c) Da versagt meine Erinnerung gerade, schau z.B. mal in den Demtröder 1, es müsste die Achse sein mit dem mittleren Trägheitsmoment, aber da bin ich mir leider recht unsicher gerade. Steht definitiv im Demtröder 1.
d) L = I * w -> ... |
|
 |
Leoniii
Gast
|
 Leoniii Verfasst am: 29. Nov 2013 00:38 Titel: Re: Trägheitstensor 3D Leoniii Verfasst am: 29. Nov 2013 00:38 Titel: Re: Trägheitstensor 3D |
 |
|
a) Berechnen Sie die Trägheitsmomente der Haupträgheitsachsen.
 = \begin{pmatrix} 2-\lambda & 1 & 1 \\ 1 & 1-\lambda & 0 \\ 1 & 0 & 1-\lambda \end{pmatrix} = -\lambda^3+4\lambda^4-3\lambda)
Ausklammern und PQ-Formel liefert die Eigenwerte
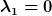


Und was sind davon jetzt genau die Haupträgheitsachsen?
b) Berechnen Sie die Haupträgheitsachsen im Koordinatensystem 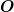
Allgemein gilt:  = 0)
 = \begin{pmatrix} 2-0 & 1 & 1 \\ 1 & 1-0 & 0 \\ 1 & 0 & 1-0 \end{pmatrix} = \vec 0)
Jetzt muss ich jeweils drei lineare Gleichungssystem lösen der Form:

Das gleiche für die restlichen zwei Eigenwerte. Daraus bekomme ich die Eigenvektoren, also die Haupträgheitsachsen im Koordinatensystem 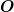 ? ?
c) Ermitteln Sie, um welche Haupträgheitsachse eine Rotation instabil wäre.
Instabil ist doch immer das mittlere Trägheitsmoment. Das Größte und das Kleinste Trägheitsmoment sind stabil und das Mittlerste ist immer instabil, aber wie kriege ich das hier heraus?
d)  aber wie soll ich daraus die Richtung bestimmen aber wie soll ich daraus die Richtung bestimmen
MfG Leoni |
|
 |
Leoniii
Gast
|
 Leoniii Verfasst am: 29. Nov 2013 23:33 Titel: Leoniii Verfasst am: 29. Nov 2013 23:33 Titel: |
 |
|
Ist das so richtig? Es wäre nett wenn mir jemand ein Feedback geben könnte, damit ich mir sicher bin auf der richtigen Route zu sein.
Danke liebe Grüße
Leoni |
|
 |
Namenloser324
Gast
|
 Namenloser324 Verfasst am: 30. Nov 2013 03:11 Titel: Namenloser324 Verfasst am: 30. Nov 2013 03:11 Titel: |
 |
|
Sieht gut aus, wobei in der letzten Zeile omega und I keine Skalare sind.
Omega ist ein Vektor und I ein Tensor bzw. eine Matrix.
Aber das mag nur ein Latexschreibfehler gewesen sein^^ |
|
 |
Leoniii
Gast
|
 Leoniii Verfasst am: 02. Dez 2013 01:21 Titel: Re: Trägheitstensor 3D Leoniii Verfasst am: 02. Dez 2013 01:21 Titel: Re: Trägheitstensor 3D |
 |
|
| Namenloser324 hat Folgendes geschrieben: | ..., wobei in der letzten Zeile omega und I keine Skalare sind.
Omega ist ein Vektor und I ein Tensor bzw. eine Matrix.
Aber das mag nur ein Latexschreibfehler gewesen sein^^ |
Ja ist auch so gemeint 

 und und 



Also folgt aus der letzten Zeile 
Und dann ist doch auch mein  und mein und mein  auch? auch? 
Was sagt mir das jetzt? Kann das so sein ich komme an dieser Stelle nicht weiter. 
Danke.
LG Leoni |
|
 |
Namenloser324
Gast
|
 Namenloser324 Verfasst am: 02. Dez 2013 01:37 Titel: Namenloser324 Verfasst am: 02. Dez 2013 01:37 Titel: |
 |
|
Die Matrix hat nicht vollen Rang, deswegen gibt es keine eindeutige Lösung.
Du kannst die erste Zeile aus den beiden unteren gewinnen.
Die dritte Zeile wird mittels "III - I + II" zu Null.
Du scheinst nen Rechenfehler gemacht zu haben, denn damit ist x3 beliebig wählbar. |
|
 |
Leoniii
Gast
|
 Leoniii Verfasst am: 02. Dez 2013 09:59 Titel: Leoniii Verfasst am: 02. Dez 2013 09:59 Titel: |
 |
|
| Namenloser324 hat Folgendes geschrieben: |
Du kannst die erste Zeile aus den beiden unteren gewinnen.
Die dritte Zeile wird mittels "III - I + II" zu Null.
Du scheinst nen Rechenfehler gemacht zu haben, denn damit ist x3 beliebig wählbar. |
Stimmt, ein Fehler ist mir unterschlichen. Ich habe meinen Fehler korrigiert dann bekomme ich auch die Nullzeile in der letzten:
 und und 



Wieso ist denn nur das  frei wählbar? Man kann auch frei wählbar? Man kann auch  frei wählen oder? frei wählen oder?
Ich wähle einfach mein und bekomme dann für mein und bekomme dann für mein  . Dann ist mein . Dann ist mein 
Und was ist jetzt dann der Vektor 
Danke,
liebe Grüße Leoni |
|
 |
Namenloser324
Gast
|
 Namenloser324 Verfasst am: 02. Dez 2013 16:06 Titel: Namenloser324 Verfasst am: 02. Dez 2013 16:06 Titel: |
 |
|
Man kann x3 beliebig wählen, da in der letzten Zeile 0*x3 = 0 steht und somit die Gleichung für jedes x3 richtig ist.
x3 ist dann einfach ein Parameter, häufig nennt man ihn z.B. lambda.
Die anderen Zeilen ergeben sich dann zu:
x2 = lambda, x1 = -lambda
Der Vektor ist dann eben lambda*(-1,1,1)
Also am einfachsten wohl (-1,1,1) für lambda = 1. |
|
 |
Leoniii
Gast
|
 Leoniii Verfasst am: 02. Dez 2013 17:35 Titel: Leoniii Verfasst am: 02. Dez 2013 17:35 Titel: |
 |
|
Und was ist jetzt der Vektor genau?
LG Leoni |
|
 |
Namenloser324
Gast
|
 Namenloser324 Verfasst am: 02. Dez 2013 17:53 Titel: Namenloser324 Verfasst am: 02. Dez 2013 17:53 Titel: |
 |
|
Hauptträgheitsachse.
Bzw. Element der Basis zu welcher der Trägheitstensor als Diagonalmatrix in Erscheinung tritt. |
|
 |
Leoniii
Gast
|
 Leoniii Verfasst am: 02. Dez 2013 21:14 Titel: Leoniii Verfasst am: 02. Dez 2013 21:14 Titel: |
 |
|
Okay nach dem Schema bekomme ich auch die anderen Hauptträgheitsachsen heraus.
Du meintest, dass bei a) die Eigenwerte bestimmen soll usw. aber was sind dann meine Trägheitsmomente.
Wie ermittle ich denn konkret um welche Hauptträgheitsachse eine Rotation instabil wäre? Es ist ist wie du ja richtig gesagt hast die mit dem mittleren Trägheitsmoment, was soll ich denn da noch berechnen?
LG Leoni |
|
 |
|


















