| Autor |
Nachricht |
gnt
Gast
|
 gnt Verfasst am: 02. Jan 2017 15:21 Titel: Konstruktion erlaubter Wellenfunktionen |
 |
|
Hallo allerseits,
gerne würde ich quantenmechanische Wellenfunktionen besser verstehen, und versuche deshalb derzeit herauszufinden, wie diese als Parameter für die Zeitentwicklung konstruiert sein müssen, damit sie physikalisch, und nicht nur mathematisch erlaubt und sinnvoll sind. - Nur falls es nicht ohnehin gleich erkennbar ist: Ich bin kein Physiker.
Konkret habe ich zwei Fragen bzw. Problemstellungen. Bei der ersten geht es darum, ob der Zustand wegen der zu erwartenden Zeitentwicklung erlaubt ist, und bei der zweiten zu erfahren, welche Regeln angewandt werden müssen. Es geht mir bei beiden nur um Eigenfunktionen von H, nicht um überlagerte Zustände.
Erstes Problem:
Bei allen Beispielen, die ich bisher gefunden habe, sind Wellenfunktionen immer so konstruiert, dass deren Zeitentwicklung an allen Orten zur gleichen Phasengeschwindigkeit (bzw. Winkelgeschwindigkeit in der komplexen Zahlenebene) führt.
Es gilt also:
}\frac{\partial (H \psi (r,t))}{\partial t} =\text{const})
Kinetische plus potentielle Energie sind also zeitlich und damit auch räumlich konstant.
Das gilt sowohl für die ebene Welle
\text{:=}e^{i (k x-\omega t)})
bei k=1 und m=1 mit
}\frac{\partial (H \psi (r,t))}{\partial t} = -\frac{i}{4})
als auch beispielsweise für den harmonischen Oszillator
\text{:=}e^{-i \frac{1}{2} \omega t} \sqrt[4]{\frac{m \omega }{\pi }} e^{-\frac{1}{2} m \omega x^2})
bei omega=1 und m=1 mit
Es gilt aber nicht für eine beispielsweise derart konstruierte Welle mit
\text{:=}\frac{e^{-\frac{x^2}{2}}}{\sqrt{2 \pi }}+1)
bei m=1 mit
}\frac{\partial (H \psi (r,t))}{\partial t} = \text{schrecklich ...})
... langer von t und x abhängiger Ausdruck. ;-)
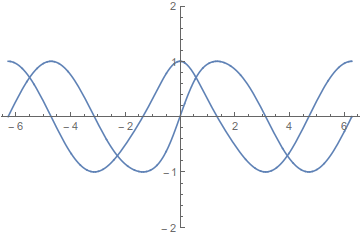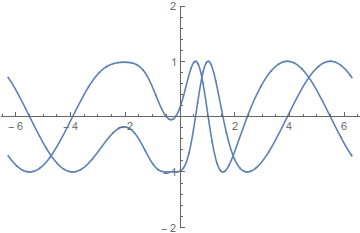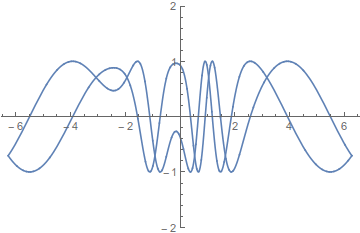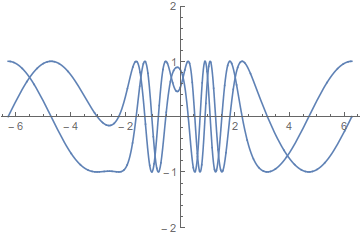
Geplottet sieht das so aus:
 http://www.physikerboard.de/files/welle_206.gif
Die Funktion "wickelt" sich also an den Stellen mit höherem k auf.
Ist so eine Funktion erlaubt, oder muss diese wie die obigen beiden Beispiele immer die Bedingung
erfüllen?
Zweites Problem:
Nur mit Hilfe des Hamilton-Operators lässt sich keine Wellenfunktion eindeutig bestimmen. Die Phase ist natürlich noch unbestimmt, in einer Dimension braucht man einen Startwert und dessen erste Ableitung, und darüber hinaus braucht man ab zwei Dimensionen eine weitere Information, nämlich in welche Richtung die Welle an jedem Ort läuft, damit die Unbestimmtheit des Laplace-Operators bzw. der Dimensionen aufgelöst wird (darin werden ja nur die Krümmungen in x-, y- und z-Richtung addiert, nicht festgelegt ist dadurch, wie viel der Krümmung auf welche Richtung entfällt). Bei der ebenen Welle legt man diese Freiheitsgrade durch den Wellenzahlvektor und beim Atom durch eine radiale Komponente und den Drehimpuls fest. Was ich aber gerne wissen würde: Wie sieht eine allgemeingültige Konstruktionsvorschrift aus? Was muss ich festlegen, sodass ich einen gültigen Eigenzustand bekomme? Meine Vermutung ist, dass man einen Teil davon aus dem Potential extrahiert; evtl. einen weiteren durch Startparameter festlegt, aber ich weiss es leider nicht.
Schon 'mal Vielen Dank für Euere Antworten!
Gruss
| Beschreibung: |
|
| Dateigröße: |
131.51 KB |
| Angeschaut: |
2045 mal |
|
|
|
 |
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18010
|
| TomS Verfasst am: 02. Jan 2017 17:31 Titel: Re: Konstruktion erlaubter Wellenfunktionen |
|
|
| gnt hat Folgendes geschrieben: | Es geht mir bei beiden nur um Eigenfunktionen von H ...
Es gilt also:
|
Im Falle von Eigenfunktionen von Eigenfunktionen gilt trivialerweise
}{\partial t} = \frac{\partial E \psi (r,t)}{\partial t} = E\, \frac{\partial \, \psi (r,t)}{\partial t} = iE^2\,\psi (r,t))
D.h. für Eigenfunktionen ist die Bedingung, dass dieser Ausdruck konstant ist, immer erfüllt.
| gnt hat Folgendes geschrieben: | | Kinetische plus potentielle Energie sind also zeitlich und damit auch räumlich konstant. |
Das würde ich so nicht schreiben, das ist einfach ein falscher Sprachgebrauch.
Kinetische und potentielle Energie sind i.A. = für ortsabhängiges Potential V(x) nicht einzeln erhalten.
Kinetische und potentielle Energie des Zustandes hängen auch nicht vom Ort ab. V(x) kann vom Ort abhängen, aber die kinetische oder potentielle Energie des Zustandes sind definiert als Erwartungswerte, d.h. als Integrale über den Ort (außer wenn V = const.)
| gnt hat Folgendes geschrieben: | Es gilt aber nicht für eine beispielsweise derart konstruierte Welle mit
|
Das ist keine Lösung der zeitabhängigen Schrödingergleichung.
| gnt hat Folgendes geschrieben: | | Es geht mir bei beiden nur um Eigenfunktionen von H, nicht um überlagerte Zustände. |
Ich denke, dein Trugschluss besteht darin, durch dieses k(x) eine Wellenfunktion einzuführen und zu glauben, dies wäre keine Superposition von Eigenfunktionen; ist es aber!
Die so definierte Wellenfunktion
\text{:=}e^{i k x})
ist keine Eigenfunktion des freien Hamiltonoperators, d.h. keine Lösung der stationären Schrödingergleichung (wie man durch zweimaligens Differenzieren sofort feststellt), und damit liefert auch eine triviale Zeitentwicklung mit konstantem omega
\text{=} \psi (\text{x},\text{t}=0)\,e^{-i\omega t)})
keine Lösung der zeitabhängigen Schrödingergleichung.
Dennoch gibt es keinen Grund, die so konstruierte Lösung für t=0 oder für spätere Zeiten auszuschließen; du musst allerdings die Zeitentwicklung korrekt berechnen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18010
|
| TomS Verfasst am: 02. Jan 2017 17:48 Titel: Re: Konstruktion erlaubter Wellenfunktionen |
|
|
| gnt hat Folgendes geschrieben: | Zweites Problem:
Nur mit Hilfe des Hamilton-Operators lässt sich keine Wellenfunktion eindeutig bestimmen. ... Was ich aber gerne wissen würde: Wie sieht eine allgemeingültige Konstruktionsvorschrift aus? |
Numerisch oder analytisch?
In beiden Fällen musst du "global" denken. Es liegt keine gewöhnliche DGL sondern eine Eigenwertgleichung vor. Du kannst insbs. nicht beliebige Startbedingungen angeben, da du i.A. (in überabzählbar vielen Fällen) keine normierbaren Lösungen erhalten wirst; d.h. formal liegt eine Lösung vor, sie ist jedoch aufgrund der fehlenden Normierbarkeit unzulässig.
Du solltest dir einmal die explizite Konstruktion z.B. für die Lösung des harmonischen Oszillators anschauen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
gnt
Gast
|
| gnt Verfasst am: 02. Jan 2017 18:33 Titel: Re: Konstruktion erlaubter Wellenfunktionen |
|
|
| TomS hat Folgendes geschrieben: | | gnt hat Folgendes geschrieben: | Es geht mir bei beiden nur um Eigenfunktionen von H ...
Es gilt also:
|
Im Falle von Eigenfunktionen von Eigenfunktionen gilt trivialerweise
D.h. für Eigenfunktionen ist die Bedingung, dass dieser Ausdruck konstant ist, immer erfüllt. |
Wunderbar! Vielen Dank!
| TomS hat Folgendes geschrieben: | | gnt hat Folgendes geschrieben: | | Kinetische plus potentielle Energie sind also zeitlich und damit auch räumlich konstant. |
Das würde ich so nicht schreiben, das ist einfach ein falscher Sprachgebrauch. |
Ja, ist richtig - ich habe da immer ein klassisches Bild mit Punktteilchen an einem Ort x im Kopf, aber das ist natürlich nicht korrekt.
| TomS hat Folgendes geschrieben: | | Dennoch gibt es keinen Grund, die so konstruierte Lösung für t=0 oder für spätere Zeiten auszuschließen; du musst allerdings die Zeitentwicklung korrekt berechnen. |
Als Überlagerungszustand ist das ja OK.
|
|
|
gnt
Gast
|
| gnt Verfasst am: 02. Jan 2017 18:52 Titel: Re: Konstruktion erlaubter Wellenfunktionen |
|
|
| TomS hat Folgendes geschrieben: | | gnt hat Folgendes geschrieben: | Zweites Problem:
Nur mit Hilfe des Hamilton-Operators lässt sich keine Wellenfunktion eindeutig bestimmen. ... Was ich aber gerne wissen würde: Wie sieht eine allgemeingültige Konstruktionsvorschrift aus? |
Numerisch oder analytisch? |
Das kann ich gar nicht beantworten - es geht mir darum, das Prinzip zu verstehen.
| TomS hat Folgendes geschrieben: | | In beiden Fällen musst du "global" denken. Es liegt keine gewöhnliche DGL sondern eine Eigenwertgleichung vor. Du kannst insbs. nicht beliebige Startbedingungen angeben, da du i.A. (in überabzählbar vielen Fällen) keine normierbaren Lösungen erhalten wirst; d.h. formal liegt eine Lösung vor, sie ist jedoch aufgrund der fehlenden Normierbarkeit unzulässig. |
Dass das Problem zur Lösung global betrachtet werden muss, ist mir klar.
Meine Vorstellung geht in die Richtung, dass man z.B. offene oder geschlossene Kurven K(s) betrachtet, entlang derer Strecke s die Welle verläuft, und eine Zwangsbedingung dafür sorgt, dass der Start- und Endpunkt der Kurve die gleiche Phase und Amplitude besitzen, und eine andere Zwangsbedingung bestimmt, wie die Krümmung senkrecht zu K(s) aussehen muss. Oder irgend so eine Beschreibung, damit, wie ich das oben schrieb, an jedem Ort klar ist, in welche Richtung k zeigt.
| TomS hat Folgendes geschrieben: | | Du solltest dir einmal die explizite Konstruktion z.B. für die Lösung des harmonischen Oszillators anschauen. |
Das harmonische Oszillator ist zwar ein nicht ganz so kompliziertes Beispiel, aber gerade die Eigenschaft, die mich am meisten interessiert, hat er leider nicht: ungebundene Zustände.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18010
|
| TomS Verfasst am: 02. Jan 2017 21:20 Titel: Re: Konstruktion erlaubter Wellenfunktionen |
|
|
| gnt hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | gnt hat Folgendes geschrieben: | Zweites Problem:
Nur mit Hilfe des Hamilton-Operators lässt sich keine Wellenfunktion eindeutig bestimmen. ... Was ich aber gerne wissen würde: Wie sieht eine allgemeingültige Konstruktionsvorschrift aus? |
Numerisch oder analytisch? |
Das kann ich gar nicht beantworten - es geht mir darum, das Prinzip zu verstehen. |
Also analytisch.
| gnt hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | In beiden Fällen musst du "global" denken. Es liegt keine gewöhnliche DGL sondern eine Eigenwertgleichung vor. Du kannst insbs. nicht beliebige Startbedingungen angeben, da du i.A. (in überabzählbar vielen Fällen) keine normierbaren Lösungen erhalten wirst; d.h. formal liegt eine Lösung vor, sie ist jedoch aufgrund der fehlenden Normierbarkeit unzulässig. |
Dass das Problem zur Lösung global betrachtet werden muss, ist mir klar.
Meine Vorstellung geht in die Richtung, dass man z.B. offene oder geschlossene Kurven K(s) betrachtet, entlang derer Strecke s die Welle verläuft, und eine Zwangsbedingung dafür sorgt, dass der Start- und Endpunkt der Kurve die gleiche Phase und Amplitude besitzen ... |
Was meinst mit "eine Strecke s läuft"?
Zeitlich betrachtet: die Welle "ist schon da", nämlich überall, und sie schwingt für jeden Punkt mit einer Amplitude als Funktion der Zeit.
Räumlich betrachtet: da ist keine Welle, die eine Strecke s entlangläuft.
Es gibt sicher keine Zwangsbedingungen. Die erlaubten Funktionen sind einfach alle normierbaren Funktionen, die die stationäre SGL lösen.
| gnt hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Du solltest dir einmal die explizite Konstruktion z.B. für die Lösung des harmonischen Oszillators anschauen. |
Das harmonische Oszillator ist zwar ein nicht ganz so kompliziertes Beispiel, aber gerade die Eigenschaft, die mich am meisten interessiert, hat er leider nicht: ungebundene Zustände. |
Aber hier siehst du, wie die Normierbarkeit die erlaubten Zustände herausfiltert.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18010
|
| TomS Verfasst am: 02. Jan 2017 21:47 Titel: |
|
|
Ich versuche nochmal zusammenzufassen, was ich bisher verstanden habe.
Gegeben ist eine System mit Hamiltonian H.
Gesucht sind zum einen Lösungen der stationären Schrödingergleichung
\phi_E = 0)
sowie Lösungen der zeitabhängigen Schrödingergleichung
= H\,\psi(t))
Letztere wird für Eigenzustände trivialerweise gelöst mittels
 = e^{-iEt}\,\phi_E)
Umgekehrt ist eine Funktion f(t), die diese triviale Zeitentwicklung nicht erfüllt, keine Eigenfunktion zu H.
Gefragt ist nun,
1) wie man zu phi kommt
2) welche Eigenschaften phi bzw. psi haben müssen, um "zulässig" zu sein.
(2) kann wie folgt zusammengefasst werden: die zulässigen Funktionen sind genau die Funktionen, die normierbar sind bzgl. des gewählten Hilbertraumes, die "genügend oft differenzierbar" sind, und für die gewisse Operatoren wie p, L, H, ... sowie deren Erwartungswerte sinnvoll definiert sind.
Weitere Einschränkungen sehe ich nicht. Insbs. liefert die Zeitentwicklung selbst keine weiteren Bedingungen, zumindest nicht für nicht-pathologische Fälle.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
gnt
Gast
|
| gnt Verfasst am: 02. Jan 2017 22:27 Titel: Re: Konstruktion erlaubter Wellenfunktionen |
|
|
| TomS hat Folgendes geschrieben: | | gnt hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | In beiden Fällen musst du "global" denken. Es liegt keine gewöhnliche DGL sondern eine Eigenwertgleichung vor. Du kannst insbs. nicht beliebige Startbedingungen angeben, da du i.A. (in überabzählbar vielen Fällen) keine normierbaren Lösungen erhalten wirst; d.h. formal liegt eine Lösung vor, sie ist jedoch aufgrund der fehlenden Normierbarkeit unzulässig. |
Dass das Problem zur Lösung global betrachtet werden muss, ist mir klar.
Meine Vorstellung geht in die Richtung, dass man z.B. offene oder geschlossene Kurven K(s) betrachtet, entlang derer Strecke s die Welle verläuft, und eine Zwangsbedingung dafür sorgt, dass der Start- und Endpunkt der Kurve die gleiche Phase und Amplitude besitzen ... |
Was meinst mit "eine Strecke s läuft"? |
Mit K meine ich eine geschlossene Kurve, also z.B. so etwas wie eine ideale Planetenbahn; s ist dann der Parameter auf dieser Bahn von 0 bis zur Länge der Bahn.
| TomS hat Folgendes geschrieben: | Räumlich betrachtet: da ist keine Welle, die eine Strecke s entlangläuft.
Es gibt sicher keine Zwangsbedingungen. Die erlaubten Funktionen sind einfach alle normierbaren Funktionen, die die stationäre SGL lösen. |
Aber wenn man K(0)=K(länge von K) setzt, führt das zu einer stetigen Funktion, wenn man solche K dicht nebeneinander packt.
Ich kann mir immer noch nicht vorstellen, dass tatsächlich jede mögliche Eigenfunktion physikalisch erlaubt ist. Gibt es dafür einen Beweis?
Vielleicht ist mir nur noch nicht klar, welche Konsequenz die Forderung der Differenzierbarkeit auf das ganze Feld bezogen hat - deshalb mein Gedanke oben mit den geschlossenen Kurven. Deren Verlauf müsste doch auch potentialabhängig sein wie bei V=0 gerade, beim Drehimpuls kreisförmig.
Irgend etwas fehlt mir da noch.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18010
|
| TomS Verfasst am: 03. Jan 2017 09:13 Titel: Re: Konstruktion erlaubter Wellenfunktionen |
|
|
Das mit den Kurven K(s) kann ich mir immer noch nicht vorstellen. Wo sollen die liegen? Und welche Bedingungen möchtest du implementieren? Das ist doch da hoc.
| gnt hat Folgendes geschrieben: | | Ich kann mir immer noch nicht vorstellen, dass tatsächlich jede mögliche Eigenfunktion physikalisch erlaubt ist. Gibt es dafür einen Beweis? |
Es gibt den experimentellen Nachweis dieser Eigenzustände, und den indirekten Nachweis, dass alle Eigenzustände benötigt werden.
| gnt hat Folgendes geschrieben: | | Vielleicht ist mir nur noch nicht klar, welche Konsequenz die Forderung der Differenzierbarkeit auf das ganze Feld bezogen hat. |
Die Differenzierbarkeit benötigst du, um p, H und letztlich die SGL definieren zu können.
|
|
|
gnt
Gast
|
| gnt Verfasst am: 03. Jan 2017 12:31 Titel: |
|
|
Ich habe mir noch Gedanken gemacht, und glaube, dass über folgendes sowohl eine Lösung als auch das/mein Problem sichtbarer wird.
Erst schreibe ich die SG so:
)\psi(r)=-\frac{1}{2m}\nabla^{2} \psi(r))
Der Faktor E-V(r) legt die Krümmung in dx+dy+dz-Richtung fest.
Bei E-V(r) handelt es sich um ein skalares Feld, nennen wir es A(r). Weil die SG wegen der Addition der Richtungsableitungen keine Richtung der Wellenfronten festlegt, muss es ein Vektorfeld B(r) geben, das die Bedingung Bx(r)+By(r)+Bz(r)=A(r) erfüllt.
Zur eindeutigen Bestimmung einer Eigenfunktion psi(r) braucht man demnach:
1. Die Schrödingergleichung
2. B(r)
3. Für einen beliebigen Punkt P psi(P)=c mit c Element C, sowie psi'(P)=i c r mit r Element R, und schliesslich einen Phasenfaktor.
Punkt 1 und 3 sind klar; die genauen Eigenschaften von Punkt 2, also B(r) interessieren mich.
Zum ersten gilt natürlich wie oben geschrieben Bx(r)+By(r)+Bz(r)=A(r).
Ausserdem muss B(r) stetig sein.
Bei einer ebenen Welle müsste B unabhängig von r sein - wohl wegen V=0.
Im Falle eines Atomorbitals müsste sich B(r) wohl abhängig von div V(r) verändern.
Ich vermute daher, dass B(r) immer eine V-Abhängigkeit aufweisen müsste.
| TomS hat Folgendes geschrieben: | | Das mit den Kurven K(s) kann ich mir immer noch nicht vorstellen. Wo sollen die liegen? Und welche Bedingungen möchtest du implementieren? Das ist doch da hoc. |
Ja, das ist nirgendwo hergeleitet.
Ich meinte das in Verbindung mit der Richtung der Wellenfronten. Wenn man den oben angenommenen Vektoren des Feldes B(r) folgt und die Krümmung von psi aufintegriert, kommt man z.B. bei Atomorbitalen mit Drehimpuls wieder an den Anfangspunkt zurück. Dort muss die Welle natürlich differenzierbar sein, also dieses Integral eine Phase von n*2pi aufweisen. So hatte ich das gemeint.
| TomS hat Folgendes geschrieben: | | gnt hat Folgendes geschrieben: | | Ich kann mir immer noch nicht vorstellen, dass tatsächlich jede mögliche Eigenfunktion physikalisch erlaubt ist. Gibt es dafür einen Beweis? |
Es gibt den experimentellen Nachweis dieser Eigenzustände, und den indirekten Nachweis, dass alle Eigenzustände benötigt werden. |
Bei gebundenen Zuständen kann ich das ohne weiteres nachvollziehen, weil man dort die Freiheitsgrade (B(r)) durch den Drehimpuls festlegt. Auch bei freien Wellenpaketen mit V=0 leuchtet mir das ein, wenn man sich auf ebene Wellen beschränkt, nicht jedoch wenn man fast jede beliebige Funktion B(r) verwenden könnte - mit Potentialen ist das noch schwieriger vorstellbar.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18010
|
| TomS Verfasst am: 03. Jan 2017 17:31 Titel: |
|
|
Zum Punkt 2) auch bei der nicht-gebundenen Zuständen kann man die Eigenfunktionen im Rahmen der Streutheorie berechnen und experimentell untersuchen; es gibt da keinen konzeptionellen Unterschied.
Zum Punkt 1) ich verstehe absolut nicht, was dieses Vektorfeld B sein soll; da steht eine skalare Gleichung, es gibt kein Vektorfeld bei derartigen DGLs.
Warum versuchst du denn nicht mal einen völlig anderen Ansatz, z.B. Fourier-Trf. / Greensche Funktionen, Transformation mittels anderer Basisfunktionen, z.B. Hermite-Funktionen, ... Störungstheorie, ... Du hängst irgendwie an einer Stelle fest, die es so letztlich gar nicht gibt. Dein Problem liegt m.E. außerhalb des üblichen Lösungsweges.
Schau doch bitte mal auf meinen Beitrag mit den Formeln und erkläre mir anhand dieser dein Problem.
|
|
|
gnt
Gast
|
| gnt Verfasst am: 03. Jan 2017 21:59 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | Du hängst irgendwie an einer Stelle fest, ... |
Zweifelsfrei hänge ich an einer Stelle fest, und es tut mir Leid, wenn mein Problem unsinnig sein sollte.
| TomS hat Folgendes geschrieben: | | ...die es so letztlich gar nicht gibt. |
Vielleicht verstehe ich es einfach nicht, keine Ahnung, aber ob es das wirklich nicht gibt, kann ich noch nicht nachvollziehen.
| TomS hat Folgendes geschrieben: | | Dein Problem liegt m.E. außerhalb des üblichen Lösungsweges. |
Ja, es liegt sicher ausserhalb des üblichen Lösungswegs, wäre aber, wie ich das jetzt sehe, meinem Verständnis der QM sehr zuträglich.
| TomS hat Folgendes geschrieben: | | Schau doch bitte mal auf meinen Beitrag mit den Formeln und erkläre mir anhand dieser dein Problem. |
Den habe ich natürlich gelesen, und bin ja völlig damit einverstanden, denke nur, dass hier noch etwas fehlt:
| TomS hat Folgendes geschrieben: | (2) kann wie folgt zusammengefasst werden: die zulässigen Funktionen sind genau die Funktionen, die normierbar sind bzgl. des gewählten Hilbertraumes, die "genügend oft differenzierbar" sind, und für die gewisse Operatoren wie p, L, H, ... sowie deren Erwartungswerte sinnvoll definiert sind.
Weitere Einschränkungen sehe ich nicht. Insbs. liefert die Zeitentwicklung selbst keine weiteren Bedingungen, zumindest nicht für nicht-pathologische Fälle. |
Jetzt habe ich versucht, ein Beispiel in 2D mit V=0 zu konstruieren, bin aber noch nicht damit zufrieden. Trotzdem stelle ich es 'mal hier herein.
Für die ebene Welle gilt:
})
Deren Krümmung wird beschrieben durch
D.h. doch zum Einsetzen in die SG:
Das Verhältnis von kx zu ky bestimmt die Richtung der ebenen Welle.
Jetzt sehe ich aber keinen Grund, warum kx und ky räumlich konstant sein sollte. Kann es denn nicht ortsabhängig sein - das meinte ich mit dem Vektorfeld, also {kx(r),ky(r)}.
Mein Versuch sieht so aus, liefert aber in der SG kein konstantes E - vielleicht liegt dort mein Denkfehler:
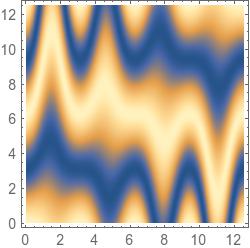
^2}{2}k\,x+(1-\frac{sin(x)^2}{2})k\,y)})
D.h. ich konstruiere für ein überall konstantes k hier als Beispiel eine sinusförmige Richtungsänderung der Wellenfronten, indem ich einmal ein stärkeres kx und dafür ein schwächeres ky, und dann wieder ein schwächeres kx und ein stärkeres ky einsetze.
Den Plot hänge ich an.
Ist so etwas grundsätzlich auszuschliessen? Auch bei V != 0?
| TomS hat Folgendes geschrieben: | | Warum versuchst du denn nicht mal einen völlig anderen Ansatz, z.B. Fourier-Trf. / Greensche Funktionen, Transformation mittels anderer Basisfunktionen, z.B. Hermite-Funktionen, ... Störungstheorie, ... |
So weit fühle ich mich noch nicht.
| Beschreibung: |
|
| Dateigröße: |
11.22 KB |
| Angeschaut: |
1916 mal |
|
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18010
|
| TomS Verfasst am: 03. Jan 2017 23:27 Titel: |
|
|
| gnt hat Folgendes geschrieben: | | Jetzt habe ich versucht, ein Beispiel in 2D mit V=0 zu konstruieren ... Für die ebene Welle gilt ... Jetzt sehe ich aber keinen Grund, warum kx und ky räumlich konstant sein sollte. Kann es denn nicht ortsabhängig sein ... liefert aber in der SG kein konstantes E |
Natürlich muss k nicht räumlich konstant sein, aber dann handelt es sich nicht um eine ebene Welle und demnach nicht um die Lösung der SGL für konstantes Potential V.
Die SGL ist aber eine Eigenwertgleichung für festes, konstantes E. Wenn beim Einsetzen einer Wellenfunktion in die SGL kein konstantes E resultiert, liegt einfach keine Lösung vor. Wenn diese Wellenfunktion dennoch eine Lösung sein soll, dann nur für ein anderes V(x).
|
|
|
gnt
Gast
|
| gnt Verfasst am: 04. Jan 2017 13:11 Titel: |
|
|
Ich habe mir die Lösung der SG noch einmal vorgestellt, und jetzt ist mir das klar.
Das war "etwas" peinlich.
Vielen Dank für Deine grosse Geduld und Deine Erklärungen!
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18010
|
| TomS Verfasst am: 04. Jan 2017 13:55 Titel: |
|
|
Heißt das, alle Unklarheiten beseitigt?
Das würde mich freuen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
gnt
Gast
|
| gnt Verfasst am: 04. Jan 2017 14:06 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | Heißt das, alle Unklarheiten beseitigt? |
Ja! 
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18010
|
| TomS Verfasst am: 04. Jan 2017 15:16 Titel: |
|
|
Gut!
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
gnt
Gast
|
| gnt Verfasst am: 05. Jan 2017 16:20 Titel: |
|
|
Gerne würde ich die Eigenfunktionen von
\psi=-\frac{1}{2m}\nabla^2\psi)
für E>0 ansehen, ohne das gleich selbst lösen zu müssen.
Kann man diese wo nachschlagen, oder hat jemand die fertige Lösung zum Hereinkopieren zur Hand?
Danke!
|
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8575
|
|
|
gnt
Gast
|
| gnt Verfasst am: 05. Jan 2017 17:22 Titel: |
|
|
Vielen Dank für die Links!
|
|
|
|
|
Registrieren
Login
FAQ
Suchen
