| Autor |
Nachricht |
Patricia.m.p
Anmeldungsdatum: 05.12.2015
Beiträge: 8
|
 Patricia.m.p Verfasst am: 05. Dez 2015 11:44 Titel: Physik - Auftriebskraft |
 |
|
Meine Frage:
Hallo,
Ich sitze an einer Aufgabe aber leider komme ich nicht weiter.
,,Ein auf einem großen See schwimmender Wu?rfel (Kantenla?nge 10 cm) taucht 2,5 cm ein. Welche Arbeit ist erforderlich, um ihn gerade unter den Wasserspiegel zu drucken?''
Meine Ideen:
Ich habe mir eine Skizze angefertigt. Zuerst taucht der Würfel 2,5cm ein - das bezeichne ich mal als x. Die kantenlänge oberhalb des Wasserspiegels wäre dann 10-x. Ich muss in dieser Aufgabe also eine Integralrechnung durchführen mit der unteren Grenze x und oberen (10-x)? Wende ich das bei der Formel für die Auftriebskraft an oder be der Berechnung der Arbeit ( w=Fxs)?
Ich bin mit hier leider nicht sicher wie ich anfangen soll ...
Eine kleine Hilfe wäre toll  |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5868
Wohnort: jwd
|
| Mathefix Verfasst am: 05. Dez 2015 13:42 Titel: |
|
|
\cdot dx)
 = A \cdot p(x))
 = \varrho \cdot g\cdot x)
 |
|
|
Patricia.m.p
Anmeldungsdatum: 05.12.2015
Beiträge: 8
|
| Patricia.m.p Verfasst am: 09. Dez 2015 20:40 Titel: |
|
|
hmm leider kann ich mit diesem Aufbau nicht so viel anfangen...
1) Ich habe mir überlegt, dass die Kraft F=Auftriebskraft-Gewichtskraft.
Die Gewichtskraft ist konstant, also Fg=m*g=V*Dichte*g=0,1^3*Dichte*g?
Was nehme ich für die Dichte des Würfels wenn die nicht angegeben ist?
2) Die Auftriebskraft hängt von der Höhe ab, die im Wasser ist also (2,5cm+x) wobei x am Anfang 0 wäre und am Ende 7,5cm?)
FA=m*g=V*Dichte(des Wassers)*g=0,1^2*(0,025+x)*1000*g
3) Zurück zur resultierenden Kraft F = Auftriebskraft-Gewichtskraft
F= 0,1^2*(0,025+x)*1000*g - 0,1^3*Dichte(des Würfels)*g
4) die Werte Zusammenfassen und dW=F(x)dx
wobei die untere Grenze 0,075 und die obere 0 wäre?
Sind meine Überlegungen richtig? Ich komme leider nicht weiter.. eine kleine Hilfe wäre toll! |
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5868
Wohnort: jwd
|
| Mathefix Verfasst am: 10. Dez 2015 12:39 Titel: |
|
|
| patricia.m.p hat Folgendes geschrieben: | hmm leider kann ich mit diesem Aufbau nicht so viel anfangen...
1) Ich habe mir überlegt, dass die Kraft F=Auftriebskraft-Gewichtskraft.
Die Gewichtskraft ist konstant, also Fg=m*g=V*Dichte*g=0,1^3*Dichte*g?
Was nehme ich für die Dichte des Würfels wenn die nicht angegeben ist?
2) Die Auftriebskraft hängt von der Höhe ab, die im Wasser ist also (2,5cm+x) wobei x am Anfang 0 wäre und am Ende 7,5cm?)
FA=m*g=V*Dichte(des Wassers)*g=0,1^2*(0,025+x)*1000*g
3) Zurück zur resultierenden Kraft F = Auftriebskraft-Gewichtskraft
F= 0,1^2*(0,025+x)*1000*g - 0,1^3*Dichte(des Würfels)*g
4) die Werte Zusammenfassen und dW=F(x)dx
wobei die untere Grenze 0,075 und die obere 0 wäre?
Sind meine Überlegungen richtig? Ich komme leider nicht weiter.. eine kleine Hilfe wäre toll! |
Der Ansatz ist doch ganz einfach:
1. Archimedisches Prinzip: Mit der Dichte ist natürlich die Dichte  des verdrängten Fluids gemeint - hätte ich vielleicht explizit schreiben sollen.
Die Dichte des Würfels spielt keine Rolle, sie ist implizit durch Angabe der Eintauchtiefe berücksichtigt.
2. Gefragt ist nach der zu verrichtenden Arbeit. W = Kraft x Weg. Die zu überwindende Kraft ist die Auftriebskraft, die wiederum vom Weg abhgängt. Der Weg ist die Strecke "x"= von der Wasseroberfläche bis zur Oberkante des Würfels.
3. Integrationsgrenzen. Da alle Angaben in cm waren, habe ich als Dimension cm gewählt. Natürlich muss die Dimension der Faktoren vor dem Integral entsprechend gewählt werden. Du kannst natürlich auch Meter als Dimension nehmen.
4. Das Integral ist leicht lösbar.
Werte einsetzen kannst Du selber.
Zuletzt bearbeitet von Mathefix am 10. Dez 2015 14:22, insgesamt 2-mal bearbeitet |
|
|
borromeus
Anmeldungsdatum: 29.12.2014
Beiträge: 509
|
| borromeus Verfasst am: 10. Dez 2015 13:59 Titel: |
|
|
| Mathefix hat Folgendes geschrieben: |
Der Ansatz ist doch ganz einfach:
1. Archimedisches Prinzip: Mit der Dicht ist natürlich die Dichte des verdrängten Fluids gemeint - hätte ich vielleicht explizit schreiben sollen.
Die Dichte des Würfels spielt keine Rolle
|
Hmm, gedanklich verstehe ich das nicht, vielleicht kannst Du mir helfen:
was wäre wenn der Würfel aus Gold ist? Dann bräuchte ich doch keine Energie.
Ich denke die Dichte des Würfels steckt hier einfach in der Zahl 7,5 des Integrals.
Wenn ich das ganz "klassich" ausrechne komme ich auf:
²
<br />
)
was natürlich keinen Anspruch auf Korrektheit hat.  ist die Eintauchtiefe ohne zusätzliche Kraft.
Rechnung falsch? Gedanke falsch? |
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5868
Wohnort: jwd
|
| Mathefix Verfasst am: 10. Dez 2015 14:17 Titel: |
|
|
| borromeus hat Folgendes geschrieben: | | Mathefix hat Folgendes geschrieben: |
Der Ansatz ist doch ganz einfach:
1. Archimedisches Prinzip: Mit der Dicht ist natürlich die Dichte des verdrängten Fluids gemeint - hätte ich vielleicht explizit schreiben sollen.
Die Dichte des Würfels spielt keine Rolle
|
Hmm, gedanklich verstehe ich das nicht, vielleicht kannst Du mir helfen:
was wäre wenn der Würfel aus Gold ist? Dann bräuchte ich doch keine Energie.
Ich denke die Dichte des Würfels steckt hier einfach in der Zahl 7,5 des Integrals.
Wenn ich das ganz "klassich" ausrechne komme ich auf:
was natürlich keinen Anspruch auf Korrektheit hat. ist die Eintauchtiefe ohne zusätzliche Kraft.
Rechnung falsch? Gedanke falsch? |
Alles falsch!
Die Dichte des Würfels ist implizit durch die Angabe der Einsinktiefe des Würfels berücksichtigt.
Wenn der Würfel aus Gold wäre, würde er ohne äussere Arbeit vollständig sinken.
Die Aufgabe ist auch ohne Integralrechnung "klassisch" lösbar - kann man im Kopf rechnen.
Das Kraft-Weg Diagramm ist ein Dreieck dessen Hypothenuse die Steigung  hat.
Die Fläche des Dreiecks ist ein Maß für die verrichtete Arbeit.
Fläche des Dreiecks: Grundlinie x Höhe/2
 = A_{Dreieck}(x) =\frac{1}{2} \cdot x\cdot A\cdot \varrho_{Wasser}\cdot g\cdot x = \frac{1}{2}\cdot A\cdot \varrho_{Wasser}\cdot g\cdot x^{2} )
Zuletzt bearbeitet von Mathefix am 10. Dez 2015 14:23, insgesamt einmal bearbeitet |
|
|
borromeus
Anmeldungsdatum: 29.12.2014
Beiträge: 509
|
| borromeus Verfasst am: 10. Dez 2015 14:23 Titel: |
|
|
Mag ja sein, aber ich sehe bei Deiner Rechnung nicht inwiefern es relevant ist ob der Würfel nun aus Holz oder aus Metall besteht.
Da wird ja eine unterschiedliche Kraft und in Folge eine unterschiedliche Energie notwendig sein.
auf Dein Edit:
Die Einsinktiefe ist aber eben 10cm-2,5cm= 7,5cm Deines Integrals.
Zuletzt bearbeitet von borromeus am 10. Dez 2015 14:27, insgesamt einmal bearbeitet |
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5868
Wohnort: jwd
|
| Mathefix Verfasst am: 10. Dez 2015 14:26 Titel: |
|
|
| borromeus hat Folgendes geschrieben: | Mag ja sein, aber ich sehe bei Deiner Rechnung nicht inwiefern es relevant ist ob der Würfel nun aus Holz oder aus Metall besteht.
Da wird ja eine unterschiedliche Kraft und in Folge eine unterschiedliche Energie notwendig sein. |
Ich habe doch gesagt, dass die Dichte des Würfels implizit durch die angegebene Einsinktiefe von 2,5 cm berücksichtigt ist.
Ehe Du weiter fragst, beschäftige Dich mit dem Archimedischen Prinzip.
Die Dichte des Würfels ist aus der Aufgabenstellung zu bestimmen:
Zuletzt bearbeitet von Mathefix am 10. Dez 2015 14:48, insgesamt 3-mal bearbeitet |
|
|
borromeus
Anmeldungsdatum: 29.12.2014
Beiträge: 509
|
| borromeus Verfasst am: 10. Dez 2015 14:28 Titel: |
|
|
auf Dein Edit:
Die Einsinktiefe ist aber eben 10cm-2,5cm= 7,5cm Deines Integrals.
und genau das habe ich ja gemutmasst. |
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5868
Wohnort: jwd
|
| Mathefix Verfasst am: 10. Dez 2015 14:39 Titel: |
|
|
| borromeus hat Folgendes geschrieben: | auf Dein Edit:
Die Einsinktiefe ist aber eben 10cm-2,5cm= 7,5cm Deines Integrals.
und genau das habe ich ja gemutmasst. |
Mein Gott. Die Einsinktiefe ist 2,5 cm!!! 7,5 cm ist der Kraftweg!! |
|
|
borromeus
Anmeldungsdatum: 29.12.2014
Beiträge: 509
|
| borromeus Verfasst am: 10. Dez 2015 14:51 Titel: |
|
|
| Mathefix hat Folgendes geschrieben: | | borromeus hat Folgendes geschrieben: | auf Dein Edit:
Die Einsinktiefe ist aber eben 10cm-2,5cm= 7,5cm Deines Integrals.
und genau das habe ich ja gemutmasst. |
Mein Gott. Die Einsinktiefe ist 2,5 cm!!! 7,5 cm ist der Kraftweg!! |
OK, sry.
Die Kommentare "Mein Gott" und "Ehe Du weiter fragst, beschäftige Dich mit dem Archimedischen Prinzip." halte ich für unfreundlich und unnütz, aber was solls.
Bei meiner Rechnung fehlt anscheinend der Faktor 1/2. Ich finde aber den Grund nicht. Ich werde das mal zusammenschreiben.... |
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5868
Wohnort: jwd
|
| Mathefix Verfasst am: 10. Dez 2015 15:07 Titel: |
|
|
| borromeus hat Folgendes geschrieben: | | Mathefix hat Folgendes geschrieben: | | borromeus hat Folgendes geschrieben: | auf Dein Edit:
Die Einsinktiefe ist aber eben 10cm-2,5cm= 7,5cm Deines Integrals.
und genau das habe ich ja gemutmasst. |
Mein Gott. Die Einsinktiefe ist 2,5 cm!!! 7,5 cm ist der Kraftweg!! |
Bei meiner Rechnung fehlt anscheinend der Faktor 1/2. Ich finde aber den Grund nicht. Ich werde das mal zusammenschreiben.... |
Der Faktor 1/2 fehlt, weil Du entweder die Dreiecksfläche unter der Kraft-Weg Funktion nicht richtig gerechnet oder falsch integriert hast.
Entschuldige meine Ungeduld, aber die Aufgabe ist wirklich simpel, wenn man in der Schule etwas aufgepasst hat ... |
|
|
borromeus
Anmeldungsdatum: 29.12.2014
Beiträge: 509
|
| borromeus Verfasst am: 10. Dez 2015 15:12 Titel: |
|
|
Also los gehts:
Um den Würfel unterzutauchen braucht man zur Gewichtskraft auch noch eine Zusatzkraft, die Summe ist die Auftriebskraft.
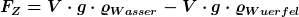
<br />
)
Der Eintauchweg ist nun:
<br />
)
Die Arbeit daher:
 \cdot x\cdot (1-\frac{x_E}{x})
<br />
)
²
<br />
)
²
<br />
)
Kann mir bitte wer sagen wo mein Rechen/Gedankenfehler ist?
Mathefix hat "dasgleiche" allerdings mit einem Faktor  . |
|
|
borromeus
Anmeldungsdatum: 29.12.2014
Beiträge: 509
|
| borromeus Verfasst am: 10. Dez 2015 15:13 Titel: |
|
|
| Mathefix hat Folgendes geschrieben: |
Entschuldige meine Ungeduld, aber die Aufgabe ist wirklich simpel, wenn man in der Schule etwas aufgepasst hat ... |
Ist schon gut, die Schule ist leider über 30 Jahre her. |
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 10. Dez 2015 15:17 Titel: |
|
|
@borromeus
Du tust so, als sei die Kraft zum Eintauchen konstant. Sie steigt aber von Null bis zu der von Dir verwendeten Kraft, ist im Mittel also nur halb so groß. Du hättest schon richtig integrieren müssen, wie von Mathefix vorgeschlagen. |
|
|
borromeus
Anmeldungsdatum: 29.12.2014
Beiträge: 509
|
| borromeus Verfasst am: 10. Dez 2015 15:25 Titel: |
|
|
Danke schön!
Es dämmert..... |
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5868
Wohnort: jwd
|
| Mathefix Verfasst am: 10. Dez 2015 17:37 Titel: |
|
|
| borromeus hat Folgendes geschrieben: | | Mathefix hat Folgendes geschrieben: |
Entschuldige meine Ungeduld, aber die Aufgabe ist wirklich simpel, wenn man in der Schule etwas aufgepasst hat ... |
Ist schon gut, die Schule ist leider über 30 Jahre her. |
Bei mir schon 55. |
|
|
|
Registrieren
Login
FAQ
Suchen
