TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18047
|
 TomS Verfasst am: 08. Sep 2015 14:29 Titel: FAQ - 3 Quarks im Proton? TomS Verfasst am: 08. Sep 2015 14:29 Titel: FAQ - 3 Quarks im Proton? |
 |
|
Im Folgenden werde ich einen kurzen Überblick geben, warum die Aussage, dass Proton und Neutron aus jeweils drei Quarks zusammengesetzt sind, zu naiv ist.
Vorab: das Proton trägt rein algebraisch die Quantenzahlen (Spin, Isospin, Color) eines Zustandes aus drei Quarks; dynamisch ist das Bild des Protons jedoch wesentlich komplexer. Algebraisch bedeutet dabei, dass die Klassifizierung der Teilchen auf Basis der Darstellungen der Spin-, Flavor- und Color-Symmetriegruppen korrekt bleibt. Dynamisch bedeutet, dass die Wechselwirkung im Rahmen der QCD beschrieben werden muss; letztere liefert nun ein deutlich komplexeres Bild.
Dazu betrachte ich einen speziellen Prozess, die sogenannte tief-inelastische Streuung von Elektronen an Protonen. Im eigentlichen Sinne streut dabei das Elektron über den Austausch eines einzelnen „virtuellen“ Photons an einem geladenen Quark in einem Proton.
Dabei kommen nun zwei Dinge zusammen: zum einen werden die Eigenschaften des Quarks im Proton (an dem das Elektron streut) durch die QCD bestimmt; zum anderen ist der Streuprozess selbst störungstheoretisch mittels der QED für asymptotisch freie Quarks beschreibbar; d.h. dieser Prozess „misst“ die komplexen Eigenschaften der QCD mittels eines „trivialen“ Prozesses aus der QED.
Tief-inelastische Streuung
Die Quarks sind als elementare Teilchen nicht direkt sichtbar. Streuexperimente bzw. Stoßprozesse an Quarks erfolgen insbs. über Streuung von Elektronen an den in einem Proton gebundenen Quarks. Tief-inelastisch bedeutet dabei, dass der der Energieübertrag vom Elektron auf das Quarks in gewissem Sinne „groß“ ist, und dass das Proton dabei nicht erhalten bleibt (bei einer elastischen Streuung bleibt die Identität der Stoßpartner bei der Streuung erhalten).
Damit kommen wir zur eigentlichen Problematik der Verteilung der Quarks im Proton:
- aus wie vielen Quarks besteht ein Nukleon?
- welchen Bruchteil des Proton-Impulses trägt ein Quark?
- welchen Bruchteil des Proton-Spin trägt ein Quark?
- was ist der Anteil der reellen bzw. der virtuelle Quarks?
- was ist der Anteil der verschiedenen Flavors?
- was ist der Anteil der Gluonen
Im Folgenden soll betrachtet werden, welche Beiträge die einzelnen Quarks zur Struktur des Nukleons leisten. Dabei wird insbs. der Unterschied zwischen dem naiven Quarkmodell und der QCD (als Quantenfeldtheorie dynamischer Quarks- und Gluonfreiheitsgrade) klar.
Kinematik
Wir betrachten den Stoßprozess eines Elektrons mit einem Nukleon:
 + N(p) \to e^\prime(k) + X(\ldots) )
Dabei bezeichnet e(k) das einfallende Elektron mit Viererimpuls k, e(k’) das auslaufende Elektron mit Viererimpuls k’, N(p) das Nukleon (Proton, Neutron) an dem gestreut wird, und X einen hadronischen Endzustand, der im einfachsten Fall (der elastischen Streuung) wieder ein Nukleon mit Impuls p’ ist, der in unserem Fall aber meist aus vielen Hadronen bestehen wird. Uns interessiert nicht, was mit den Hadronen im Einzelnen passiert, sondern wir konzentrieren uns ausschließlich auf das gestreute Elektron e(k’). Nur dieses wird auch im Detektor gemessen und ausgewertet.
k, k’, p, q bezeichnen dabei Viererimpulse. Nun definieren wir folgende Variable
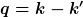
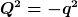
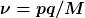
² )
q ist der Viererimpulsübertrag des Elektrons.
(Das ausgetauschte Photon ist virtuell; man sieht hier sehr schön, dass das Viererimpulsquadrat q² nicht Null ist wie bei einem realen Photon)
Im Ruhesystem des Protons gilt
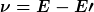
der Energieverlust des Elektrons (wobei die Elektronmasse m vernachlässigt wird)
^2 = -4EE\prime \sin^2\theta/2)
mit dem Streuwinkel theta des Elektrons.
Nun führt man die dimensionslose Variable x ein:
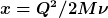
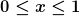
Das Regime der tief-inelastischen Streuung definiert man als den kinematischen Bereich mit
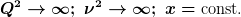
Die physikalische Annahme ist nun, dass im Bereich der tief-inelastischen Streuung die asymptotische Freiheit der QCD gilt und man lediglich Korrekturen zum naiven Quarkmodell zu erwarten hat. Die führenden Beiträge sind dann jeweils die freien Feldoperatoren der QCD (die das naive Quarkmodell reproduzieren); die weiteren Beiträge sind Korrekturen der QCD.
Strukturfunktionen
Man betrachtet nun die Streuamplitude sowie den experimentell bestimmbaren differentiellen Streuquerschnitt. Der Streuquerschnitt ist ein Maß für die Reaktionsfläche des Nukleons, die das Elektron als „Querschnittsfläche“ beim Stoß „sieht“. Der differentielle Streuquerschnitt ist ein Maß der Reaktion der Streuung des Elektrons in einen Raumwinkel Omega und in ein Energieintervall E hinein. Der totale Streuquerschnitt ist wiederum das Integral über alle Raumwinkel (über eine Kugeloberfläche) und alle Energien E des gestreuten Elektrons.
Für den differentiellen Streuquerschnitt gilt die Proportionalität
\,f(q,E,E^\prime) \, w_{\mu\nu}(k,k^\prime) \, W^{\mu\nu} (p,q) )
alpha bezeichnet die (energieabhängige) starke Kopplungskonstante, f eine kinematische Funktion, w einen ebenfalls kinematischen Tensor. W(p,q) ist ein hadronischer Tensor, der die nichttrivialen Informationen bzgl. der Nukleonstruktur enthält.
Im Bereich der tief-inelastischen Streuung sollte die Streuung von der Reaktion eines einzelnen, quasi-freien Quarks mit dem Elektron dominiert sein; die nachfolgende (sehr komplizierte) Wechselwirkung des gestreuten Quarks im hadronischen Endzustand X sollte keine Rückwirkung auf den Streuwinkel des Elektrons mehr haben.
Für den hadronischen Tensor W(p,q) findet man eine kovariante Zerlegung, in der nur noch zwei skalare Funktionen
,\;F^2(x,Q^2) )
die als Quark- Strukturfunktionen bezeichnet werden und die die Informationen über die elektrische und magnetische Struktur der Nukleonen tragen, bzw. die Auskunft darüber geben, wie sich diese Struktur darstellt, wenn sie von einem Elektron mit Viererimpulsübertrag q = k - k’ „getestet“ wird. Die Struktur des Nukleons erscheint abhängig davon, mit welchem Viererimpuls q das Experiment durchgeführt wird.
Man interpretiert dabei x als den Bruchteil des Nukleon-Impulses, den das streuende Quark im Stoß auf das Elektron überträgt. Im naiven Quarkmodell mit drei Quarks je Nukleon erwartet man, dass die Strukturfunktionen einen scharfen Peak aufweisen:
 \sim \delta(x - 1/3) )
Das physikalische Bild des Nukleons (in dem betrachteten Limes) ist also im Wesentlichen das einer Schar lose gekoppelter, sich parallel bewegender Quarks mit näherungsweise gleichem Impulsanteil x = 1/3.
Als Spezialfall kann man die elastische Streuung betrachten, dass nämlich X wiederum ein Nukleon ist und das Streu-Target erhalten bleibt. Man findet dann, dass die Strukturfunktionen die Nukleon-Formfaktoren reproduzieren, die die el.-mag. Stromdichte im Impulsraum, sowie speziell für Q²=0 die elektrische Ladung sowie das magnetische Moment beschreiben (die Formfaktoren entsprechen bei geeigneter Wahl des Koordinatensystems den Fouriertransformierten der el.-mag. Stromdichten).
Ergebnisse zum Aufbau der Nukleonen
Zur Erinnerung: wir betrachten den tiefinelastischen Bereich
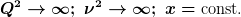
Wir nehmen an, dass in diesem Bereich lediglich die Streuung eines Elektrons an einem quasi-freien Quark dominiert und dass die WW des gestreuten Quarks im hadronischen Endzustand X vernachlässigbar ist.
Bjorken-Scaling
Betrachtet man die Q²-Abhängigkeit dieser Strukturfunktionen, so beobachtet man für große Q², dass die Strukturfunktionen tatsächlich näherungsweise unabhängig von Q² werden, d.h.
 \to F^n(x) )
Damit sind die Strukturfunktionen in diesem Regime unabhängig von einer äußeren Massenskala; dieses Verhalten weist auf punktförmige Konstituenten hin, eben die Quarks. Man nennt dieses Verhalten Bjorken Scaling.
Zur Erläuterung: für die elektromagnetischen Formfaktoren des Protons existiert eine Energieskala, die die entsprechenden Funktionen mitbestimmt. Dieser Energieskala entspricht eine Längenskala, die wiederum die „Größe“ des Protons bestimmt. Im Falle von punktförmigen Teilchen verschwinden diese Längenskala und damit die Energieskala. Dies entspricht der Unabhängigkeit von Q².
Callan-Gross-Beziehung für Spin ½
Zunächst folgt aus der Struktur des hadronischen Tensors eine Beziehung für die Strukturfunktionen in Abhängigkeit vom Spin der Quarks. Experimentell ist die Callan-Gross-Beziehung
 = F^2(x) )
gut erfüllt; aus ihr kann man ableiten, dass es sich bei den Quarks um Fermionen mit Spin ½ handelt.
Allgemeines zu den Strukturfunktionen
Zur Berechnung und Interpretation der Strukturfunktionen nimmt man an, dass die QCD zwar die Impuls- bzw. Energieverteilung des streuenden Quarks über die Strukturfunktionen bestimmt, man geht jedoch weiter davon aus, dass während der Streuung selbst das Quark sich wie ein freies Teilchen verhält. Dies ist Ausdruck der asymptotischen Freiheit der Quarks für große Impulsüberträge Q². Damit ist der Streuprozess selbst störungstheoretisch beschreibbar und man erwartet, dass das Elektron direkt die beiden Strukturfunktionen „misst“.
Tatsächlich funktioniert diese Interpretation hervorragend. Aus den so gewonnen Daten können die Strukturfunktionen rekonstruiert und die Substruktur des Nukleons interpretiert werden. Zunächst überlegt man sich, wie die Strukturfunktionen aussehen müssten, wenn tatsächlich das naive Quarkmodel mit drei punktförmigen Quarks realisiert wäre. Anschließend betrachtet man Korrekturen der QCD zum naiven Quarkmodell.
Summenregeln
Aus den Strukturfunktionen können über bestimmte Modellannahmen die Strukturfunktionen direkt für die einzelnen Quarksorten abgeleitet werden. Außerdem kann man sogenannte Summenregeln ableiten, das sind Regeln, die den Wert bestimmter x-Integrale die Strukturfunktionen vorgeben. Einige dieser Summenregeln gelten auch in der QCD exakt, andere erfahren Korrekturen
Zunächst spaltet man die Strukturfunktion in einzelne Funktion f je Flavor sowie nach Quarks und Antiquarks auf.
Als Beispiel für eine Summenregel betrachte man die Integrale für die Impulse
 )
sowie die Flavor-Quantenzahlen u,d,s:
 - f_{\bar{u}}(x)] = 2 )
 - f_{\bar{d}}(x)] = 1 )
 - f_{\bar{d}}(x)] = 0 )
Setzt man die Impuls-Summenregel gleich Eins, so entspricht dies der naiven Erwartung, dass zum Gesamtimpuls ausschließlich Quarks beitragen. Diese Impuls-Summenregel ist in der QCD deutlich verletzt! Wir hatten angenommen, dass das Nukleon eine reine Quark-Struktur hat, d.h. wir haben Strukturfunktionen für die Gluonen vernachlässigt. Es zeigt sich, dass die drei Quarksorten u,d,s nur ca. 0.44 beitragen, die entsprechenden Antiquarks ca. 0.07. Tatsächlich werden also gemäß der QCD nur ca. 50% des Nukleon-Impulses durch die Quarks getragen, die Gluonen tragen ebenfalls ca. 50% bei.
Die Summenregeln für Gesamt-Isospin und -Strangeness entsprechen dem naiven Quarkmodell und müssen auch in der QCD exakt erfüllt sein, da das Proton rein algebraisch exakt die Isospin- und Strangeness-Quantenzahlen entsprechend u = 2, d = 1, s = 0 trägt.
Sea-Quarks
Nimmt man nun zunächst an, das Proton bestünde aus drei nicht wechselwirkenden Quarks, so wäre
 \sim \delta(x - 1/3) )
Im Falle von rein gluonisch gebunden Quarks erwartet man eine Verbreiterung dieser Funktion um den Wert 1/3, allerdings mit
 = F^n(1) = 0)
Entgegen diesem naiven Modell stellt man jedoch fest, dass auch Quarks mit x = 0 einen wesentlichen Beitrag zu den Strukturfunktionen leisten.
D.h. die Quarks können sicher nicht als näherungsweise freie Quarks betrachtet werden, wie man sie aus dem naiven Quarkmodell erwartet. Stattdessen tragen auch sogenannte virtuelle oder Sea-Quarks bei. Diese Quark-See ist ein Effekt des QCD-Vakuums, d.h. bereits im Vakuum sind „virtuelle Quark-Antiquark-Paare“ vorhanden, die im Rahmen der tief-inelastischen Streuung „sichtbar“ werden. Für kleine x dominieren diese Sea-Quark Effekte sogar und tragen auch messbar zu Summenregeln bei.
Man stellt außerdem fest, dass zu diesen Sea-Quarks auch s- und anti-s Quarks einen nicht zu vernachlässigenden Beitrag leisten (die s-Quarks kommen im naiven Quarkmodell gemäß Strangeness s = 0 im Nukleon nicht vor)
Im naiven Quarkmodell erwartet man außerdem, dass nur u- und d-Quarks zur elektrischen Ladung (Proton: Q=1, Neutron: Q=0) beitragen; in der QCD stellt man fest, dass auch die entsprechenden Antiquarks sowie die s- und anti-s-Quarks wesentlich sind.
Die Annahme, dass die Sea-Quarks bzgl. u und d symmetrisch wären, erfährt eine leichte Korrektur. Die Annahme, dass s-Quarks keinen Beitrag leisten, wird in der QCD korrigiert; die s-Quarks sind dabei natürlich reine Sea-Quarks.
Scaling violations
Gluon structure functions
Spin structure
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|















