| Autor |
Nachricht |
Spitzname_123
Gast
|
 Spitzname_123 Verfasst am: 02. Jan 2015 18:49 Titel: Ausbreitung einer ebenen Welle in einem Ferrit (anisotrop) Spitzname_123 Verfasst am: 02. Jan 2015 18:49 Titel: Ausbreitung einer ebenen Welle in einem Ferrit (anisotrop) |
 |
|
Meine Frage:
Frohes Neues.
Die Aufgabestellung lautet. Der Wellenvektor k sei parallel zur Z-Achse. Bestimmen sie die möglichen Geschwindikeiten (Ich denke Gruppen und Phasengeschw.) und möglichen Polarisationen der Welle.
In dem Medium gelten:


Meine Ideen:
Ich habe nun folgende Wellengleichung hergeleitet
\cdot \overrightarrow{k}
<br />
) . .
Im Vakuum kann man ja hier die Felder gegeneinander Wegkürzen, was hier leider nicht so einfach geht.Ich kann natürlich 
nutzen allerdings sind da ja aufgrund der Anisotropie die x und y Komponenten gemischt in den Termen der Dispersionsrelation und ich kann nicht so einfach  berechnen. Allerdings habe ich auch keine andere Idee. berechnen. Allerdings habe ich auch keine andere Idee. |
|
 |
adadsdas
Gast
|
 adadsdas Verfasst am: 02. Jan 2015 19:00 Titel: adadsdas Verfasst am: 02. Jan 2015 19:00 Titel: |
 |
|
Da steht, dass k parallel zu z-Achse ist, dann vereinfacht sich deine Gleichung erheblich und ) kannst du selbstverständlich immernoch nutzen, das ist letztendlich nur eine Definition. kannst du selbstverständlich immernoch nutzen, das ist letztendlich nur eine Definition. |
|
 |
ohneplan123
Gast
|
 ohneplan123 Verfasst am: 08. Feb 2015 19:47 Titel: Re: Ausbreitung einer ebenden Welle in einem Ferrit (Anisotr ohneplan123 Verfasst am: 08. Feb 2015 19:47 Titel: Re: Ausbreitung einer ebenden Welle in einem Ferrit (Anisotr |
 |
|
| Spitzname_123 hat Folgendes geschrieben: |
Ich habe nun folgende Wellengleichung hergeleitet
\cdot \overrightarrow{k}
<br />
) . .
|
Da ich zuletzt an einer ähnlichen Aufgabe saß, würde ich gern versuchen diese zu lösen und würde mich freuen, wenn mal jemand drüberschaut.
Die Wellengleichung kann ich in Indexschreibweise so schreiben:


)
Daraus folgt mit k_1=0, k_2=0 und k_3 = k:
)
)
Ist das erstmal so richtig? Wie komme ich jetzt auf die Dispersionsrelation. Klar Determinante berechnen, aber wie löse ich dass dan nach \omega auf? Dabei bräuchte ich bitte Hilfe. 
Danke  |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 08. Feb 2015 19:56 Titel: jh8979 Verfasst am: 08. Feb 2015 19:56 Titel: |
 |
|
|
Die Aufgabe geht komplett analog zu dem anderen Thread und wie dort, sag ich Dir hier: Du kannst nicht immer dieselben Bezeichnungen für die Summationsindizes verwenden (letzter Term). |
|
 |
ohneplan123
Gast
|
 ohneplan123 Verfasst am: 08. Feb 2015 20:37 Titel: ohneplan123 Verfasst am: 08. Feb 2015 20:37 Titel: |
 |
|
| jh8979 hat Folgendes geschrieben: | | Die Aufgabe geht komplett analog zu dem anderen Thread und wie dort, sag ich Dir hier: Du kannst nicht immer dieselben Bezeichnungen für die Summationsindizes verwenden (letzter Term). |
Ja deswegen wollte ich nochmal zur Sicherheit eine Aufgabe machen!
letzter Term ok.
Also sowas:

Stimmt, sonst gibt es Probleme bei der Summation
Passt es so?
Aber die Matrizenform müsste so gestimmt haben, oder? |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 08. Feb 2015 21:06 Titel: jh8979 Verfasst am: 08. Feb 2015 21:06 Titel: |
 |
|
| ohneplan123 hat Folgendes geschrieben: |

|
Nein.
Linke Seite: Dein freier Index heisst in den anderen Termin i und nicht l.
Rechte Seite: Ist nicht die Linke Seite.
| Zitat: |
Aber die Matrizenform müsste so gestimmt haben, oder? |
Nein. |
|
 |
ohneplan123
Gast
|
 ohneplan123 Verfasst am: 08. Feb 2015 21:12 Titel: ohneplan123 Verfasst am: 08. Feb 2015 21:12 Titel: |
 |
|
| jh8979 hat Folgendes geschrieben: | | ohneplan123 hat Folgendes geschrieben: |

|
Nein.
Linke Seite: Dein freier Index heisst in den anderen Termin i und nicht l.
Rechte Seite: Ist nicht die Linke Seite.
| Zitat: |
Aber die Matrizenform müsste so gestimmt haben, oder? |
Nein. |
Also ist

in Ordnung?
nur mein Umschreiben dann war nicht in Ordnung?

Kannst du mir nochmal eplizit sagen, in welchem Faktor der Fehler ist? ich sehe es nicht.  |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 08. Feb 2015 21:13 Titel: jh8979 Verfasst am: 08. Feb 2015 21:13 Titel: |
 |
|
|
H_j ist doch nicht gleich mu_{ij}B_j (wie immer: Indizes!). |
|
 |
ohneplan123
Gast
|
 ohneplan123 Verfasst am: 08. Feb 2015 21:19 Titel: ohneplan123 Verfasst am: 08. Feb 2015 21:19 Titel: |
 |
|
| jh8979 hat Folgendes geschrieben: | | H_j ist doch nicht gleich mu_{ij}B_j (wie immer: Indizes!). |
Aber warum nicht? verstehe ich nicht. H ist die Matrix µ multipliziert mit dem Spaltenvektor B und genau das steht doch da.
Was ist also falsch? |
|
 |
ohneplan123
Gast
|
 ohneplan123 Verfasst am: 08. Feb 2015 21:22 Titel: ohneplan123 Verfasst am: 08. Feb 2015 21:22 Titel: |
 |
|
| ohneplan123 hat Folgendes geschrieben: | | jh8979 hat Folgendes geschrieben: | | H_j ist doch nicht gleich mu_{ij}B_j (wie immer: Indizes!). |
Aber warum nicht? verstehe ich nicht. H ist die Matrix µ multipliziert mit dem Spaltenvektor B und genau das steht doch da.
Was ist also falsch? |
Hab es gerafft!
Da muss stehen:

richtig? |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 08. Feb 2015 21:28 Titel: jh8979 Verfasst am: 08. Feb 2015 21:28 Titel: |
 |
|
| ohneplan123 hat Folgendes geschrieben: |
Da muss stehen:

richtig? |
Die Formel ist richtig, aber da steht dann nicht H_i, sondern H_j.
PS: Es gibt einige einfache Regeln, an denen man sofort sehen kann, ob man einen Fehler gemacht hat:
1. Jeder Summand (auf beiden Seiten der Gleichung) hat exakt dieselben einfach auftretenden Indizes (die "freien" Indizes sind also in jedem Summanden Gleich).
2. In jedem Summand tritt kein Index mehr als doppelt auf. D.h. es gibt nie einen Term der Form k_i \mu_{ij} B_i.
(1. ist eine exakte Aussage. Die 2. stimmt nicht immer, aber der Fall dass ein Index mehr als 2mal in einem regulären Term auftaucht ist extrem(!!) selten.) |
|
 |
ohneplan123
Gast
|
 ohneplan123 Verfasst am: 08. Feb 2015 22:05 Titel: ohneplan123 Verfasst am: 08. Feb 2015 22:05 Titel: |
 |
|
| jh8979 hat Folgendes geschrieben: | | ohneplan123 hat Folgendes geschrieben: |
Da muss stehen:

richtig? |
Die Formel ist richtig, aber da steht dann nicht H_i, sondern H_j.
|
Wie meinst du das?
soll ich quasi noch umformen zu:

und dass dann in die Ausgangsformel einsetzen?
Aber dann hätte ich ja dass problem mit zu oft vorkommenden Indizes.
Also zum ganzen Term,
da steht ein Skalarprodukt von H und k:
Da ich das über Summation definiere brauch ich ja den Summationsindex
Also:

Ist das so richtig?
und das andere k ist dann wieder mit freiem Index.
Ansonsten würde ich dich bitten mir mal die Formel hinzuschreiben, die du raushast und mir vielleicht mal zu erklären, wie du da rangehst! |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 08. Feb 2015 22:13 Titel: jh8979 Verfasst am: 08. Feb 2015 22:13 Titel: |
 |
|
Wie Du richtig hingeschrieben hast gilt:

d.h. die i-te Komponente des Vektors H erhaelt man, indem man die Matrix mu mit dem Vektor B multipliziert und davon die i-te Komponente nimmt. Der Index j ist ein Summationsindex, also beliebig.
Die j-te Komponente lautet aus demselben Grund

wobei ich den Summationsindex (der beliebig ist) jetzt einfach "Blaubart" genannt habe (i,k,l,m,p,.. wären auch alles gute Namen, nur j nicht, da j in dieser Gleichung schon vorkommt).
(Und zur Besseren Lesbarkeit hab ich ein Komma zwischen die Indizes j und Blaubart von mu geschrieben. Das hat ansonsten aber keine Bedeutung.) |
|
 |
ohneplan123
Gast
|
 ohneplan123 Verfasst am: 08. Feb 2015 22:23 Titel: ohneplan123 Verfasst am: 08. Feb 2015 22:23 Titel: |
 |
|
| jh8979 hat Folgendes geschrieben: | Wie Du richtig hingeschrieben hast gilt:

d.h. die i-te Komponente des Vektors H erhaelt man, indem man die Matrix mu mit dem Vektor B multipliziert und davon die i-te Komponente nimmt. Der Index j ist ein Summationsindex, also beliebig.
Die j-te Komponente lautet aus demselben Grund

wobei ich den Summationsindex (der beliebig ist) jetzt einfach "Blaubart" genannt habe (i,k,l,m,p,.. wären auch alles gute Namen, nur j nicht, da j in dieser Gleichung schon vorkommt).
(Und zur Besseren Lesbarkeit hab ich ein Komma zwischen die Indizes j und Blaubart von mu geschrieben. Das hat ansonsten aber keine Bedeutung.) |
Ok, soweit so gut, das verstehe ich erstmal 
Ich möchte ja aber irgendwann die B-Komponente ausklammern, deswegen muss ich ja in jedem Term den gleichen Summationsindex bekommen oder sehe ich das falsch?
Deswegen würde mich mal interessieren, wie du das für die ganze gleiche machst und dazu eine kurze erklärung, vielleicht machts dann klick, wie man am besten vorgeht. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 08. Feb 2015 22:30 Titel: jh8979 Verfasst am: 08. Feb 2015 22:30 Titel: |
 |
|
Einfach Umbennen, so dass B in jedem Summanden denselben Index hat. Summationsindizes kannst Du nennen wie Du willst:
 |
|
 |
ohneplan123
Gast
|
 ohneplan123 Verfasst am: 08. Feb 2015 22:55 Titel: ohneplan123 Verfasst am: 08. Feb 2015 22:55 Titel: |
 |
|
Also so:


Aber was ändert sich jetzt da an der Matrixdarstellung? Mein Promblem ist noch etwas das umswitschen zwischen der Indexschreibweise und der normalenschreibweise. Ist es jetzt so, dass ich quasi, die j-te Zeile von \mu mit der j-ten Komponente von k multipliziere und anschließend die komplette matrix mit der Komponente k_i? Ist das richtig? |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 09. Feb 2015 00:10 Titel: jh8979 Verfasst am: 09. Feb 2015 00:10 Titel: |
 |
|
Nein, die freien Indizes sind nicht richtig. Und ansonsten die (i,m)-te Komponente der Matrix die B multipliziert ist gegeben durch was immer dasteht.
PS: Sorry, ich hatte nicht gesehen dass Du schon den Spezialfall (0,0,k) eingesetzt hattest. Dann ist die Matrixform glaub ich richtig... |
|
 |
ohneplan123
Gast
|
 ohneplan123 Verfasst am: 09. Feb 2015 01:15 Titel: ohneplan123 Verfasst am: 09. Feb 2015 01:15 Titel: |
 |
|
| jh8979 hat Folgendes geschrieben: | Nein, die freien Indizes sind nicht richtig. Und ansonsten die (i,m)-te Komponente der Matrix die B multipliziert ist gegeben durch was immer dasteht.
PS: Sorry, ich hatte nicht gesehen dass Du schon den Spezialfall (0,0,k) eingesetzt hattest. Dann ist die Matrixform glaub ich richtig... |
Was stimmt an den freien Indizes nicht? bei denen war ich mir sicher, dass die ok sind.
Schreib es mir bitte mal richtig hin, damit ich sehe, was das Problem ist. Ich dreh mich im Kreis. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 09. Feb 2015 01:18 Titel: jh8979 Verfasst am: 09. Feb 2015 01:18 Titel: |
 |
|
|
Zwei Terme haben einen freien Index i, der erste einen freien Index j ... so schwer wie Du das hier anstellst ist das ja nun wirklich nicht... |
|
 |
ohneplan123
Gast
|
 ohneplan123 Verfasst am: 09. Feb 2015 01:35 Titel: ohneplan123 Verfasst am: 09. Feb 2015 01:35 Titel: |
 |
|

jetzt richtig?
Doch es ist so schwer, weil ich es nicht gewohnt bin. Deswegen wäre es mir wirklich lieb gewesen, wenn du mir einfach kurz aufgeschrieben hättest, wie du sowas machst. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 09. Feb 2015 01:46 Titel: jh8979 Verfasst am: 09. Feb 2015 01:46 Titel: |
 |
|
| ohneplan123 hat Folgendes geschrieben: |
Doch es ist so schwer, weil ich es nicht gewohnt bin. |
Nein. Zählen ist nicht so schwer. Also Indizes zählen:
| Zitat: |

|
Erster Term -> (l,l,i,j,i,m,m)
Zweiter Term -> (i,j,j,m,m)
Dritter Term -> (i,m,m)
Die einfach auftretenden, freien Indizes sind mal fett gedruckt. Das sind doch nicht dreimal dieselben...
Was soll die Gleichung also heissen? Die i-te Komponente des Vektors der durch die Multiplikation entsteht? Wieso ist dann kein i im ersten Term? Die j-te Komponente des Vektors? wieso ist dann ein freies i in den letzten beiden Termen? ... Dir ist offensichtlich gar nicht bewusst, was Du da hinschreibst. Was bedeutet denn ein Ausdruck wie 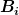 oder oder  ? ? |
|
 |
ohneplan123
Gast
|
 ohneplan123 Verfasst am: 09. Feb 2015 02:00 Titel: ohneplan123 Verfasst am: 09. Feb 2015 02:00 Titel: |
 |
|
[quote="jh8979"] | ohneplan123 hat Folgendes geschrieben: |
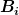 oder oder  ? ? |
B_i bedeutet die i_te Komponente des Vektors B
\mu_{sr}B_r bedeutet die s-te Komponente des Vektors, der bei der Multiplikation der Maxtrix M (s-Zeilen und r Spalten) mit den Spaltenvektor B_r (r-Komponenten) entsteht
Also:

??????
Ok, gemerkt. Freier Index immer gleich, bei Summationen aufpassen, vorallem wenn mehr als 2 Dinge multipliziert werden! 
Mein Problem war, dass ich erst alles auf H_j bringen wollte und dann alles auf B_j deswegen bin ich durcheinander gekommen. Ich merk mir jetzt, dass erst am Ende wichtig ist, wenn ich weiß, was ich ausklammern will. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 09. Feb 2015 07:57 Titel: Re: Ausbreitung einer ebenden Welle in einem Ferrit (Anisotr jh8979 Verfasst am: 09. Feb 2015 07:57 Titel: Re: Ausbreitung einer ebenden Welle in einem Ferrit (Anisotr |
 |
|
Bei dem ganzen Index-Gewuerge ist mir ganz entgangen, dass dies falsch ist:
| Spitzname_123 hat Folgendes geschrieben: |

|
Es gilt
 |
|
 |
ohneplan123
Gast
|
 ohneplan123 Verfasst am: 09. Feb 2015 19:35 Titel: Re: Ausbreitung einer ebenden Welle in einem Ferrit (Anisotr ohneplan123 Verfasst am: 09. Feb 2015 19:35 Titel: Re: Ausbreitung einer ebenden Welle in einem Ferrit (Anisotr |
 |
|
| jh8979 hat Folgendes geschrieben: | Bei dem ganzen Index-Gewuerge ist mir ganz entgangen, dass dies falsch ist:
| Spitzname_123 hat Folgendes geschrieben: |

|
Es gilt
 |
HAHA...welche Ironie, gut aber die Indexdiskussion war ja nicht umsonst.
Also neu:
 \vec k)
Mit Indizes:

Es gelten diese Relationen:

Einsetzen und Umstellen liefert die Wellengleichung:

H_j =\hat A \vec H)
Stimmt das so?
Damit die Matrixgleichung wieder nicht-triviale Lösungen hat, muss die Determinante wieder 0 werden.
Das werd ich jetzt in Angriff nehmen, nachdem du mir bestätigt hast, dass ich es jetzt scheinbar kapiert hab mit den Indizes.
Eine frage hab ich noch:
ist nun

eine Matrix aus allen Kombinationen (quasi Tensorprodukt) oder muss auch hier über j summieren? dann wäre es ja ein Vektor. Ist mir nicht so ganz klar, da ja ja aber eigentlich mein Summationsindex ist, verwirrt mich das ein kleines bisschen. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 09. Feb 2015 19:55 Titel: Re: Ausbreitung einer ebenden Welle in einem Ferrit (Anisotr jh8979 Verfasst am: 09. Feb 2015 19:55 Titel: Re: Ausbreitung einer ebenden Welle in einem Ferrit (Anisotr |
 |
|
Ausgehend von der ersten Gleichung sieht das jetzt viel besser aus mit den Indizes. Kleiner Fehler:
| ohneplan123 hat Folgendes geschrieben: |
H_j =\hat A \vec H)
|
Bei dem letzten Gleichheitszeichen steht links ein freier Index i, rechts aber keiner. Korrekt wäre etwas wie:
H_j =(\hat A \vec H)_i)
| Zitat: |
ist nun

eine Matrix aus allen Kombinationen (quasi Tensorprodukt) |
Das ist eine Matrix mit Indizes i und j, die mit dem Vektor H multipliziert wird (daher das H_j). Das Ergebnis davon ist dann ein Vektor mit Index i. |
|
 |
ohneplan123
Gast
|
 ohneplan123 Verfasst am: 11. Feb 2015 00:11 Titel: ohneplan123 Verfasst am: 11. Feb 2015 00:11 Titel: |
 |
|
Super!
Dann bekomme ich die Matrix bestimmt zu:


Dann steht in der Aufgabenstellung, das der Wellenvektor parallel zur z-Achse verläuft:
)

Die Determinante muss verschwinden:
^2\left(-\epsilon\omega^2\mu_z\right) - \left(\epsilon\omega^2\alpha\right)^2\left(-\epsilon\omega^2\mu_z\right))
 - \left(\epsilon\omega^2\alpha\right))
 = k^2)
Dispersionsrelation:
= \frac k {\sqrt{\epsilon\left(\alpha + \mu\right)}})
Phasengeschwindigkeit:
}})
Gruppengeschwindigkeit:
}})
Ist das so in Ordnung?
Zu den Polarisationen der Welle, wie bestimme ich die? Hier soll ich ja jetzt nicht wie in der Aufgabe mit dem E-Feld mögliche Polarisationsvektoren finden oder? Sondern soll sicherlich herausfinden wann zirkular und wann linear polarisiert, oder? Wie muss ich vorgehen? |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 11. Feb 2015 00:13 Titel: jh8979 Verfasst am: 11. Feb 2015 00:13 Titel: |
 |
|
| ohneplan123 hat Folgendes geschrieben: |
Zu den Polarisationen der Welle, wie bestimme ich die? Hier soll ich ja jetzt nicht wie in der Aufgabe mit dem E-Feld mögliche Polarisationsvektoren finden oder? Sondern soll sicherlich herausfinden wann zirkular und wann linear polarisiert, oder? Wie muss ich vorgehen? |
Wo ist denn da der Unterschied? |
|
 |
ohneplan123
Gast
|
 ohneplan123 Verfasst am: 11. Feb 2015 00:18 Titel: ohneplan123 Verfasst am: 11. Feb 2015 00:18 Titel: |
 |
|
| jh8979 hat Folgendes geschrieben: | | ohneplan123 hat Folgendes geschrieben: |
Zu den Polarisationen der Welle, wie bestimme ich die? Hier soll ich ja jetzt nicht wie in der Aufgabe mit dem E-Feld mögliche Polarisationsvektoren finden oder? Sondern soll sicherlich herausfinden wann zirkular und wann linear polarisiert, oder? Wie muss ich vorgehen? |
Wo ist denn da der Unterschied? |
Eben das Frage ich ja, weil mir das nicht ganz klar ist. Ich kann doch für eine Ebene Welle für das B-Feld ansetzen:
})
Wenn ich da Polarisationsvektoren jetzt bestimme, heißt dann linear polarisiert, nur von einer Koordinate abhängig? Und zirkular polarisiert ist dann von 2 Variablen abhängig? |
|
 |
ohneplan123
Gast
|
 ohneplan123 Verfasst am: 12. Feb 2015 10:12 Titel: ohneplan123 Verfasst am: 12. Feb 2015 10:12 Titel: |
 |
|
|
@jh8979: kannst du hierzu nochmal kurz etwas sagen? danke |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 12. Feb 2015 10:42 Titel: jh8979 Verfasst am: 12. Feb 2015 10:42 Titel: |
 |
|
| ohneplan123 hat Folgendes geschrieben: |
Wenn ich da Polarisationsvektoren jetzt bestimme, heißt dann linear polarisiert, nur von einer Koordinate abhängig? Und zirkular polarisiert ist dann von 2 Variablen abhängig? |
Nein. Du musst gucken wie sich die Richtung des B-Feldes mit der Zeit verändert.
Siehe z.B. hier:
http://www.physikerboard.de/topic,41848,-polarisation-einer-welle.html |
|
 |
ohneplan123
Gast
|
 ohneplan123 Verfasst am: 12. Feb 2015 17:57 Titel: ohneplan123 Verfasst am: 12. Feb 2015 17:57 Titel: |
 |
|
Ok, alles klar.
Aber was bedeutet der Polarisationsvektor dann überhaupt?
Ich meine die Ausbreitung und die Art der Polarisation ist ja offensichtlich gegeben dur die e-Fkt. Was gibt der Polarisationsvektor dann an? Die Richtung der Polarisation? Die Amplitude der Wellenfunktion? Ist mir irgendwie nicht klar |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 13. Feb 2015 11:10 Titel: jh8979 Verfasst am: 13. Feb 2015 11:10 Titel: |
 |
|
| ohneplan123 hat Folgendes geschrieben: |
Aber was bedeutet der Polarisationsvektor dann überhaupt?
Ich meine die Ausbreitung und die Art der Polarisation ist ja offensichtlich gegeben dur die e-Fkt. Was gibt der Polarisationsvektor dann an? Die Richtung der Polarisation? Die Amplitude der Wellenfunktion? Ist mir irgendwie nicht klar |
Der Betrag |) des gesamten Feldes des gesamten Feldes ) gibt die Amplitude an, die Richtung von gibt die Amplitude an, die Richtung von ) die Polarization. die Polarization. |
|
 |
|


















