| Autor |
Nachricht |
MMchen60
Anmeldungsdatum: 31.01.2021
Beiträge: 207
Wohnort: Heilbronn
|
 MMchen60 Verfasst am: 01. März 2022 08:08 Titel: Winkelbeschleunigung und Drehmoment MMchen60 Verfasst am: 01. März 2022 08:08 Titel: Winkelbeschleunigung und Drehmoment |
 |
|
Hallo liebe Forumsgemeinde,
ich bräuchte mal kurzfristig einen Tipp für einen Ansatz für folgende Aufgabe:
Eine Welle von 40 mm Durchmesser und 600 mm Länge wird durch das Moment M=0,308 Nm in 1,2 s aus der Ruhe auf 3000
1/min beschleunigt. Berechne die Masse der Welle.
Gegeben sind die jeweiligen Formeln der Trägheitsmomente J_x und J_y.
Mein Ansatz wäre zunächst mal vom gegebenen Drehmoment auf J_y (senkrecht zur Drehachse) zu schließen. Mir fehlt momentan die Verbindung vom gegebenen Moment über die Winkelbeschleunigung und die Winkelgeschwindigkeit zum Trägheitsmoment zu kommen.
Vielen Dank für Antwort.
|
|
 |
roycy
Anmeldungsdatum: 05.05.2021
Beiträge: 961
|
 roycy Verfasst am: 01. März 2022 08:53 Titel: Re: Winkelbeschleunigung und Drehmoment roycy Verfasst am: 01. März 2022 08:53 Titel: Re: Winkelbeschleunigung und Drehmoment |
 |
|
| MMchen60 hat Folgendes geschrieben: | Hallo liebe Forumsgemeinde,
Eine Welle
|
Aus welchem Werkstoff/Material besteht denn diese Welle?
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5852
|
 Myon Verfasst am: 01. März 2022 09:08 Titel: Re: Winkelbeschleunigung und Drehmoment Myon Verfasst am: 01. März 2022 09:08 Titel: Re: Winkelbeschleunigung und Drehmoment |
 |
|
| MMchen60 hat Folgendes geschrieben: | Mir fehlt momentan die Verbindung vom gegebenen Moment über die Winkelbeschleunigung und die Winkelgeschwindigkeit zum Trägheitsmoment zu kommen.
Vielen Dank für Antwort. |
Bei einer konstanten Winkelbeschleunigung mit  gilt gilt

M ist das Drehmoment und I das Massenträgheitsmoment bez. der Drehachse. Hier soll wahrscheinlich von einer Welle mit homogener Massenverteilung ausgegangen werden. Damit besteht ein eindeutiger Zusammenhang zwischen Masse, Radius der Welle und dem Trägheitsmoment (vgl. Trägheitsmoment einer Scheibe).
|
|
 |
MMchen60
Anmeldungsdatum: 31.01.2021
Beiträge: 207
Wohnort: Heilbronn
|
 MMchen60 Verfasst am: 01. März 2022 09:43 Titel: Re: Winkelbeschleunigung und Drehmoment MMchen60 Verfasst am: 01. März 2022 09:43 Titel: Re: Winkelbeschleunigung und Drehmoment |
 |
|
| Myon hat Folgendes geschrieben: |
Bei einer konstanten Winkelbeschleunigung mit  gilt gilt
 |
Also wäre in obigem Fall:

Mit 
Somit 
und mit gegebenem  )
käme man dann auf die Masse?
|
|
 |
Ich
Anmeldungsdatum: 11.05.2006
Beiträge: 913
Wohnort: Mintraching
|
 Ich Verfasst am: 01. März 2022 10:10 Titel: Ich Verfasst am: 01. März 2022 10:10 Titel: |
 |
|
|
Was bitte willst du mit dem Trägheitsmoment senkrecht zur Drehachse?
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5863
Wohnort: jwd
|
 Mathefix Verfasst am: 01. März 2022 10:37 Titel: Mathefix Verfasst am: 01. März 2022 10:37 Titel: |
 |
|
Da es sich um eine Rotationsbewegung handelt, ist nicht das äquatoriale , sondern das polare Massenträgheitsmoment I_p relevant.

Aus Symmetriegründen ist

|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5863
Wohnort: jwd
|
 Mathefix Verfasst am: 01. März 2022 10:40 Titel: Re: Winkelbeschleunigung und Drehmoment Mathefix Verfasst am: 01. März 2022 10:40 Titel: Re: Winkelbeschleunigung und Drehmoment |
 |
|
| roycy hat Folgendes geschrieben: | | MMchen60 hat Folgendes geschrieben: | Hallo liebe Forumsgemeinde,
Eine Welle
|
Aus welchem Werkstoff/Material besteht denn diese Welle? |
Die Angabe des Werkstoffs wird nicht benötigt.
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5863
Wohnort: jwd
|
 Mathefix Verfasst am: 01. März 2022 10:48 Titel: Re: Winkelbeschleunigung und Drehmoment Mathefix Verfasst am: 01. März 2022 10:48 Titel: Re: Winkelbeschleunigung und Drehmoment |
 |
|
| MMchen60 hat Folgendes geschrieben: | | Myon hat Folgendes geschrieben: |
Bei einer konstanten Winkelbeschleunigung mit  gilt gilt
 |
Also wäre in obigem Fall:

Mit 
Somit 
und mit gegebenem  )
käme man dann auf die Masse? |
Überprüfe die Einheit von 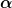
Berechne m allgemein und setze Zahlenwerte erst in die Endgleichung ein.
|
|
 |
MMchen60
Anmeldungsdatum: 31.01.2021
Beiträge: 207
Wohnort: Heilbronn
|
 MMchen60 Verfasst am: 02. März 2022 08:32 Titel: Re: Winkelbeschleunigung und Drehmoment MMchen60 Verfasst am: 02. März 2022 08:32 Titel: Re: Winkelbeschleunigung und Drehmoment |
 |
|
| Mathefix hat Folgendes geschrieben: |
Überprüfe die Einheit von 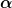
Berechne m allgemein und setze Zahlenwerte erst in die Endgleichung ein. |
Hallo danke, aber wenn ich jetzt nicht konsequent die Formel bis zum Ende umgestellt habe und dann erst die Zahlen einsetze, was meinst du mit "Überprüfe die Ei9nheit von 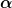 ? Ist ? Ist  nicht richtig ode meinst du den von mir errechneten Wert? nicht richtig ode meinst du den von mir errechneten Wert?
Danke.
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5852
|
 Myon Verfasst am: 02. März 2022 08:42 Titel: Re: Winkelbeschleunigung und Drehmoment Myon Verfasst am: 02. März 2022 08:42 Titel: Re: Winkelbeschleunigung und Drehmoment |
 |
|
| MMchen60 hat Folgendes geschrieben: | (...) was meinst du mit "Überprüfe die Ei9nheit von 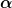 ? Ist ? Ist  nicht richtig ode meinst du den von mir errechneten Wert? nicht richtig ode meinst du den von mir errechneten Wert? |
 hat die Einheit rad/s, hat die Einheit rad/s,  somit die Einheit rad/s^2. somit die Einheit rad/s^2.
|
|
 |
MMchen60
Anmeldungsdatum: 31.01.2021
Beiträge: 207
Wohnort: Heilbronn
|
 MMchen60 Verfasst am: 02. März 2022 09:37 Titel: Re: Winkelbeschleunigung und Drehmoment MMchen60 Verfasst am: 02. März 2022 09:37 Titel: Re: Winkelbeschleunigung und Drehmoment |
 |
|
| Myon hat Folgendes geschrieben: |
 hat die Einheit rad/s, hat die Einheit rad/s,  somit die Einheit rad/s^2. somit die Einheit rad/s^2. |
Oooh, ja, Knöpfe auf den Augen. Danke.
|
|
 |
roycy
Anmeldungsdatum: 05.05.2021
Beiträge: 961
|
 roycy Verfasst am: 02. März 2022 22:00 Titel: Re: Winkelbeschleunigung und Drehmoment roycy Verfasst am: 02. März 2022 22:00 Titel: Re: Winkelbeschleunigung und Drehmoment |
 |
|
| MMchen60 hat Folgendes geschrieben: | | Myon hat Folgendes geschrieben: |
Bei einer konstanten Winkelbeschleunigung mit  gilt gilt
 |
|
Ich denke das MTM brerechnet sich aus I = m*r²/2, mag mich aber irren.
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5863
Wohnort: jwd
|
 Mathefix Verfasst am: 03. März 2022 08:25 Titel: Re: Winkelbeschleunigung und Drehmoment Mathefix Verfasst am: 03. März 2022 08:25 Titel: Re: Winkelbeschleunigung und Drehmoment |
 |
|
| roycy hat Folgendes geschrieben: | | MMchen60 hat Folgendes geschrieben: | | Myon hat Folgendes geschrieben: |
Bei einer konstanten Winkelbeschleunigung mit  gilt gilt
 |
|
Ich denke das MTM brerechnet sich aus I = m*r²/2, mag mich aber irren. |


M = 0,308 Nm
d= 0,04 m
n =3.000 1/min
T = 1,2 s

|
|
 |
roycy
Anmeldungsdatum: 05.05.2021
Beiträge: 961
|
 roycy Verfasst am: 03. März 2022 12:24 Titel: roycy Verfasst am: 03. März 2022 12:24 Titel: |
 |
|
| Mathefix hat Folgendes geschrieben: | Da es sich um eine Rotationsbewegung handelt, ist nicht das äquatoriale , sondern das polare Massenträgheitsmoment I_p relevant.

Aus Symmetriegründen ist
 |
Nö, hier geht es um das Massenträgheitsmoment und nicht um das polare Trägheitsmoment.
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5863
Wohnort: jwd
|
 Mathefix Verfasst am: 03. März 2022 12:47 Titel: Mathefix Verfasst am: 03. März 2022 12:47 Titel: |
 |
|
| roycy hat Folgendes geschrieben: | | Mathefix hat Folgendes geschrieben: | Da es sich um eine Rotationsbewegung handelt, ist nicht das äquatoriale , sondern das polare Massenträgheitsmoment I_p relevant.

Aus Symmetriegründen ist
 |
Nö, hier geht es um das Massenträgheitsmoment und nicht um das polare Trägheitsmoment. |
Ich hatte geschrieben polares Massenträgheitsmoment.
Abhängig von der Bezugsachse gibt es beliebig viele Massenträgheitsmomente.
Welches schlägst Du vor? Bitte mit Formel oder noch besser Herleitung.
|
|
 |
roycy
Anmeldungsdatum: 05.05.2021
Beiträge: 961
|
 roycy Verfasst am: 03. März 2022 16:05 Titel: roycy Verfasst am: 03. März 2022 16:05 Titel: |
 |
|
[quote="Mathefix"] | roycy hat Folgendes geschrieben: | | Mathefix hat Folgendes geschrieben: | |
Ich hatte geschrieben polares Massenträgheitsmoment.
Abhängig von der Bezugsachse gibt es beliebig viele Massenträgheitsmomente.
Welches schlägst Du vor? Bitte mit Formel oder noch besser Herleitung. |
Hatte ich bereits: m*r²/2, da es sich um eine "Welle" handeln soll.
Unter "Welle" versteht man( im Maschinenbau) etwas Bestimmtes hinsichtlich der Rotationsachse.
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5863
Wohnort: jwd
|
 Mathefix Verfasst am: 03. März 2022 16:42 Titel: Mathefix Verfasst am: 03. März 2022 16:42 Titel: |
 |
|
[quote="roycy"] | Mathefix hat Folgendes geschrieben: | | roycy hat Folgendes geschrieben: | | Mathefix hat Folgendes geschrieben: | |
Ich hatte geschrieben polares Massenträgheitsmoment.
Abhängig von der Bezugsachse gibt es beliebig viele Massenträgheitsmomente.
Welches schlägst Du vor? Bitte mit Formel oder noch besser Herleitung. |
Hatte ich bereits: m*r²/2, da es sich um eine "Welle" handeln soll.
Unter "Welle" versteht man( im Maschinenbau) etwas Bestimmtes hinsichtlich der Rotationsachse. |
Um welchen Typ von Massenträgheitsmoment handelt es sich bei I =1/2 * m *r^2 ? Leite das doch mal her.
Danke für den HInweis. Dass es sich um eine Welle handelt, darauf wäre ich echt nicht gekommen.
|
|
 |
roycy
Anmeldungsdatum: 05.05.2021
Beiträge: 961
|
 roycy Verfasst am: 03. März 2022 16:47 Titel: roycy Verfasst am: 03. März 2022 16:47 Titel: |
 |
|
[quote="Mathefix"] | roycy hat Folgendes geschrieben: | | Mathefix hat Folgendes geschrieben: | | roycy hat Folgendes geschrieben: | | Mathefix hat Folgendes geschrieben: | |
Ich hatte geschrieben polares Massenträgheitsmoment.
Abhängig von der Bezugsachse gibt es beliebig viele Massenträgheitsmomente.
Welches schlägst Du vor? Bitte mit Formel oder noch besser Herleitung. |
. |
Um welchen Typ von Massenträgheitsmoment handelt es sich bei I =1/2 * m *r^2 ? Leite das doch mal her.
Danke für den HInweis. Dass es sich um eine Welle handelt, darauf wäre ich echt nicht gekommen. |
Gerne, weil du aus einigen Dingen gern ein Problem kreierst.
Braucht man nicht. Dafür gibt es fertige Formeln in Bezug auf die Hauptachse einer Welle bei einer Drehmomentübertragung. Oder postest du jedes mal, wenn du Integralrechnung anwendest die Herleitung derselben auch noch?
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5863
Wohnort: jwd
|
 Mathefix Verfasst am: 03. März 2022 17:18 Titel: Mathefix Verfasst am: 03. März 2022 17:18 Titel: |
 |
|
| roycy hat Folgendes geschrieben: |
Gerne, weil du aus einigen Dingen gern ein Problem kreierst.
Braucht man nicht. Dafür gibt es fertige Formeln in Bezug auf die Hauptachse einer Welle bei einer Drehmomentübertragung. Oder postest du jedes mal, wenn du Integralrechnung anwendest die Herleitung derselben auch noch? |
In der Aufgabenstellung steht, das I_x und I_y, also die äquatorialen MTM's, gegeben sind.
Benötigt wird wegen Rotation das polare MTM
IP = I_x + I_y
Die Richtigkeit hattest Du angezweifelt und damit diese unnötige Diskussion in Gang gesetzt.
PS
Wenn man die Herleitungen nicht beherrscht, also die Zusammenhänge nicht kennt und stumpf irgendwelche Formeln anwendet, kann man sich schwer verkalkulieren.
Meinerseits Ende der sinnlosen Diskussion.
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5785
Wohnort: Heidelberg
|
 as_string Verfasst am: 03. März 2022 17:39 Titel: as_string Verfasst am: 03. März 2022 17:39 Titel: |
 |
|
| Mathefix hat Folgendes geschrieben: | | roycy hat Folgendes geschrieben: |
Gerne, weil du aus einigen Dingen gern ein Problem kreierst.
Braucht man nicht. Dafür gibt es fertige Formeln in Bezug auf die Hauptachse einer Welle bei einer Drehmomentübertragung. Oder postest du jedes mal, wenn du Integralrechnung anwendest die Herleitung derselben auch noch? |
In der Aufgabenstellung steht, das I_x und I_y, also die äquatorialen MTM's, gegeben sind. |
Da bin ich mir nicht so ganz sicher. Du weißt ja nicht, was mit x und y gemeint ist (wobei Du recht hast, dass man häufig die Symmetrieachse doch in die z-Achse legen würde, aber das ist ja nicht unbedingt immer so). Also ich verstehe seinen Text so, als ob I_x eventuell die Rotationsachse sein könnte, die man braucht, weil er explizit erwähnt, dass er das senkrecht dazu, nämlich I_y, genommen hat, das klingt für mich so, wenn zwei gegeben sind, dass das andere eben nicht senkrecht dazu ist. Aber wer weiß... Da bräuchte man eventuell eine Skizze vom TE oder so... In meinen Augen würde es ja auch keinen sinnvollen Grund geben, zweimal das Trägheitsmoment bezüglich jeweils zwei senkrechten Achsen zur Rotationsachse anzugeben, die ja wegen der Symmetrie logischerweise so wie so gleich sein müssen.
| Mathefix hat Folgendes geschrieben: | Benötigt wird wegen Rotation das polare MTM
IP = I_x + I_y |
Das wollte ich Dich so wie so fragen: Du schreibst das so, als ob das irgendwie ein allgemein gültiges Gesetz wäre. Mir ist klar, dass es bei einem Zylinder sicherlich so ist. Aber allgemein kann es ja nicht gelten, weil z. B. eine homogene Kugel (oder Kugelschale) ja bezüglich jeder Achse dasselbe Trägheitsmoment hat. Meinst Du das nur für diesen Spezialfall eines Zylinders oder ist das allgemeiner gültig?
Gruß
Marco
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5785
Wohnort: Heidelberg
|
 as_string Verfasst am: 03. März 2022 17:46 Titel: as_string Verfasst am: 03. März 2022 17:46 Titel: |
 |
|
Ich muss mich korrigieren. Das mit 1/4 mr^2 gilt nur für eine dünne Scheibe. Wir kommst Du auf diese Summe dann?
Also hier muss ich roycy Recht geben: Das Trägheitsmoment für einen Zylinder entlang seiner Symmetrie-Achse ist 1/2 mr^2 und da es eine Welle ist, soll sie wohl entsprechend rotieren. Ich weiß nicht, was Du aus den anderen Trägheitsmomenten genau versuchst auszurechnen, aber die Summe ist auf jeden Fall das falsche, weil die Welle ja definitiv nicht als dünne Scheibe verstanden werden kann.
Gruß
Marco
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5863
Wohnort: jwd
|
 Mathefix Verfasst am: 03. März 2022 18:49 Titel: Mathefix Verfasst am: 03. März 2022 18:49 Titel: |
 |
|
| as_string hat Folgendes geschrieben: | Ich muss mich korrigieren. Das mit 1/4 mr^2 gilt nur für eine dünne Scheibe. Wir kommst Du auf diese Summe dann?
Also hier muss ich roycy Recht geben: Das Trägheitsmoment für einen Zylinder entlang seiner Symmetrie-Achse ist 1/2 mr^2 und da es eine Welle ist, soll sie wohl entsprechend rotieren. Ich weiß nicht, was Du aus den anderen Trägheitsmomenten genau versuchst auszurechnen, aber die Summe ist auf jeden Fall das falsche, weil die Welle ja definitiv nicht als dünne Scheibe verstanden werden kann.
Gruß
Marco |
Polares Massenträgheitsmoment
x und y stehen aufeinander senkrecht
 = dm \cdot R^{2} = dI_p )

Äquatoriale Massenträgheitsmomente I_x und I_y bezogen auf die Rotationsachse

Symmetrie


qed
|
|
 |
roycy
Anmeldungsdatum: 05.05.2021
Beiträge: 961
|
 roycy Verfasst am: 03. März 2022 19:15 Titel: Welle roycy Verfasst am: 03. März 2022 19:15 Titel: Welle |
 |
|
| as_string hat Folgendes geschrieben: | | Mathefix hat Folgendes geschrieben: | | roycy hat Folgendes geschrieben: |
|
In der Aufgabenstellung steht, das I_x und I_y, also die äquatorialen MTM's, gegeben sind. |
IP = I_x + I_y |
Das wollte ich Dich so wie so fragen: Du schreibst das so, als ob das irgendwie ein allgemein gültiges Gesetz wäre. Mir ist klar, dass es bei einem Zylinder sicherlich so ist. Aber allgemein kann es ja nicht gelten, weil z. B. eine homogene Kugel (oder Kugelschale) ja bezüglich jeder Achse dasselbe Trägheitsmoment hat. Meinst Du das nur für diesen Spezialfall eines Zylinders oder ist das allgemeiner gültig?
Gruß
Marco[/quote]
Ingenieure machen bei einer "Welle" nicht so viel Gedöns, sonst werden sie mit ihrer Arbeit nicht fertig und beschäftigen sich ungern mit ziemlich nutzlosen Dingen.
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5852
|
 Myon Verfasst am: 03. März 2022 19:19 Titel: Myon Verfasst am: 03. März 2022 19:19 Titel: |
 |
|
| Mathefix hat Folgendes geschrieben: | Symmetrie
 |
Ich glaube, da geht es um Flächenträgheitsmomente? Welche Bedeutung sollen denn I_x und I_y haben, zum Beispiel hier bei einem Zylinder? Im Addieren von Massenträgheitsmomenten bezüglich verschiedener Achsen sehe ich keinen Sinn.
|
|
 |
roycy
Anmeldungsdatum: 05.05.2021
Beiträge: 961
|
|
 |
roycy
Anmeldungsdatum: 05.05.2021
Beiträge: 961
|
 roycy Verfasst am: 04. März 2022 18:10 Titel: MTM roycy Verfasst am: 04. März 2022 18:10 Titel: MTM |
 |
|
| Mathefix hat Folgendes geschrieben: | | roycy hat Folgendes geschrieben: |
|
Wenn man die Herleitungen nicht beherrscht, also die Zusammenhänge nicht kennt und stumpf irgendwelche Formeln anwendet, kann man sich schwer verkalkulieren.
Meinerseits Ende der sinnlosen Diskussion. |
Wenn "Musjö" Eiffel so kompliziert gedacht/gehandelt hätte wie du, würde er am Eiffel-Turm immer noch herumrechnen u. Ableitungen erstellen.
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5785
Wohnort: Heidelberg
|
 as_string Verfasst am: 07. März 2022 14:48 Titel: as_string Verfasst am: 07. März 2022 14:48 Titel: |
 |
|
| Mathefix hat Folgendes geschrieben: | | as_string hat Folgendes geschrieben: | Ich muss mich korrigieren. Das mit 1/4 mr^2 gilt nur für eine dünne Scheibe. Wir kommst Du auf diese Summe dann?
Also hier muss ich roycy Recht geben: Das Trägheitsmoment für einen Zylinder entlang seiner Symmetrie-Achse ist 1/2 mr^2 und da es eine Welle ist, soll sie wohl entsprechend rotieren. Ich weiß nicht, was Du aus den anderen Trägheitsmomenten genau versuchst auszurechnen, aber die Summe ist auf jeden Fall das falsche, weil die Welle ja definitiv nicht als dünne Scheibe verstanden werden kann.
Gruß
Marco |
Polares Massenträgheitsmoment
x und y stehen aufeinander senkrecht
 = dm \cdot R^{2} = dI_p )

Äquatoriale Massenträgheitsmomente I_x und I_y bezogen auf die Rotationsachse

Symmetrie


qed |
OK, danke schön für die Erklärung! Ich kannte das tatsächlich in der Form noch nicht, hab mich aber bisher auch noch nicht viel mit Flächenträgheitsmomenten beschäftigt.
Wenn ich Dich richtig verstehe bedeutet das: Wenn ich den Querschnitt einer prismenförmigen Welle kenne und für die Querschnittsfläche die beiden axialen Flächenträgheitsmomente bezüglich zweier senkrechter Achsen, dann bekomme ich das polare Trägheitsmoment (und damit auch das Trägheitsmoment der Welle entlang ihrer Rotationsachse), indem ich die beiden axialen addiere.
Ich bin aber immer noch skeptisch, dass das Ix und Iy von der Aufgabe wirklich für die axialen Flächenträgheitsmoment steht, allerdings wäre das wohl tatsächlich möglich, keine Ahnung...
Gruß
Marco
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5852
|
 Myon Verfasst am: 08. März 2022 08:57 Titel: Myon Verfasst am: 08. März 2022 08:57 Titel: |
 |
|
| as_string hat Folgendes geschrieben: | | Wenn ich Dich richtig verstehe bedeutet das: Wenn ich den Querschnitt einer prismenförmigen Welle kenne und für die Querschnittsfläche die beiden axialen Flächenträgheitsmomente bezüglich zweier senkrechter Achsen, dann bekomme ich das polare Trägheitsmoment (und damit auch das Trägheitsmoment der Welle entlang ihrer Rotationsachse), indem ich die beiden axialen addiere. |
Dass bei einem dünnen, ebenen Körper gilt

vergleiche auch hierzu. Dabei sind  zwei Massenträgheitsmomente zu zwei beiliebigen, senkrecht zu einander stehenden Achsen in der Fläche, und zwei Massenträgheitsmomente zu zwei beiliebigen, senkrecht zu einander stehenden Achsen in der Fläche, und 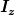 zur Achse senkrecht zur Fläche und durch den Schnittpunkt der anderen Achsen. Dass dies so sein muss, leuchtet auch unmittelbar ein, vgl. auch die Erklärung im Artikel. zur Achse senkrecht zur Fläche und durch den Schnittpunkt der anderen Achsen. Dass dies so sein muss, leuchtet auch unmittelbar ein, vgl. auch die Erklärung im Artikel.
Bei einem Körper mit konstanter Querschnittsfläche kann das helfen, wenn sich kartesische Koordinaten besser eignen als Polar- bzw. Zylinderkoordinaten (z.B. bei einem T-Balken o.ä.).
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5863
Wohnort: jwd
|
 Mathefix Verfasst am: 08. März 2022 11:18 Titel: Mathefix Verfasst am: 08. März 2022 11:18 Titel: |
 |
|
@Myon
Vielen Dank!
Genau das hatte ich geschrieben.
Habe Marco nicht geantwortet, da ich keine weiteren substanzlosen Kommentare von anderer Stelle provozieren wollte.
|
|
 |
|















