| Autor |
Nachricht |
ineke
Gast
|
 ineke Verfasst am: 20. Jun 2014 15:22 Titel: Wie überprüfe ich anhand des Bildes die Knoten-und Maschenre |
 |
|
Meine Frage:
Hallo, ich möchte gerne wissen wie ich anhand des Bildes Gleichungen zur Maschen-und Knotenregel aufstellen um diese zu überprüfen.
Würde mich sehr über eine Antwort freuen.
Meine Ideen:
Ich weiß das die Ströme hinsichtlich der Knotenregel alle durch Punkt A fließen. ...
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 20. Jun 2014 15:28 Titel: |
|
|
| ineke hat Folgendes geschrieben: | | Hallo, ich möchte gerne wissen wie ich anhand des Bildes Gleichungen zur Maschen-und Knotenregel aufstellen um diese zu überprüfen. |
Welches Bild?
|
|
|
ineke
Anmeldungsdatum: 20.06.2014
Beiträge: 11
|
| ineke Verfasst am: 20. Jun 2014 15:44 Titel: |
|
|
Wie stelle ich hier denn ein Bild rein? 
|
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
| as_string Verfasst am: 20. Jun 2014 15:50 Titel: |
|
|
Wo Du jetzt angemeldet bist, hast Du doch bei "Antwort schreiben" unter dem Nachrichtentext einen Bereich "Attachment hinzufügen". Wenn die Bilddatei nicht zu groß ist, kannst Du das doch damit recht einfach machen, oder?
Gruß
Marco
|
|
|
ineke
Anmeldungsdatum: 20.06.2014
Beiträge: 11
|
| ineke Verfasst am: 20. Jun 2014 15:52 Titel: |
|
|
|
Die Datei ist viel zu groß. Keine Ahnung wir ich das sonst machen soll
|
|
|
ineke
Anmeldungsdatum: 20.06.2014
Beiträge: 11
|
| ineke Verfasst am: 21. Jun 2014 10:38 Titel: Bild |
|
|
Bild
| Beschreibung: |
|
Download |
| Dateiname: |
Schaltkreis.jpg |
| Dateigröße: |
28.35 KB |
| Heruntergeladen: |
530 mal |
|
|
|
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
| isi1 Verfasst am: 21. Jun 2014 11:24 Titel: |
|
|
Hier kannst ein Kochrezept für solche Aufgaben finden, ineke.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
|
ineke
Anmeldungsdatum: 20.06.2014
Beiträge: 11
|
| ineke Verfasst am: 21. Jun 2014 11:49 Titel: |
|
|
|
Das bringt mir leider nichts, da ich damit nicht klar komme ...
|
|
|
ineke
Anmeldungsdatum: 20.06.2014
Beiträge: 11
|
| ineke Verfasst am: 21. Jun 2014 13:01 Titel: |
|
|
|
Kann mir bitte bitte jemand helfen, wie ich bei dem Chaos die Gleichungen richtig aufstellen?
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 21. Jun 2014 14:21 Titel: |
|
|
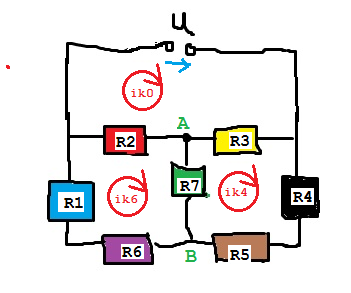
Was isi1 Dir gezeigt hat, sind zwei Verfahren für Fortgeschrittene, bei denen entweder nur die Knotenpunktgleichungen oder nur die Maschengleichungen benötigt werden. Du willst aber offenbar das Zweigstromverfahren anwenden, bei dem die Anzahl der nötigen Gleichungen gleich der Anzahl der unbekannten Zweigströme ist. Die Anzahl der Zweige ist (einschließlich des Zweiges mit der Spannungsquelle) z=6, nämlich
- der Zweig mit der Spannungsquelle und dem Strom Iges
- der Zweig mit R1+R6 und dem Strom I1
- der Zweig mit R2 und dem Strom I2
- der Zweig mit R3 und dem Strom I3
- der Zweig mit R4+R5 und dem Strom I4
- der Zweig mit R7 und dem Strom I7
Es handelt sich um ein Netzwerk mit k=4 Knoten, d.h. es gibt z-1=3 unabhängige Knotengleichungen. Welche der 4 möglichen Knotengleichungen Du weglässt, ist egal.
Die restlichen Gleichungen müssen also m=z-(k-1) Maschengleichungen sein, hier m=6-(4-1)=3. Zur Überprüfung der Unabhängigkeit der Maschengleichungen gibt es das Verfahren des vollständigen Baums oder ein vereinfachtes Verfahren, bei dem man jede Masche, für die man den Maschensatz aufgestellt hat, an einer beliebigen Stelle gedanklich auftrennt. Alle weiteren Maschenumläufe dürfen nicht über so eine gedachte Trennstelle laufen.
Eine gewisse Ordnung in Dein Chaos bringst Du, indem Du jedem Strom eine Richtung zuordnest, die prinzipiell beliebig sein kann. Es ist jedoch sinnvoll, in einfachen Fällen wie dem vorliegenden die physikalisch "richtigen" Stromrichtungen vorzugeben.
Bei einer Richtung der Versorgungsspannung von rechts nach links fließt
Iges von links nach rechts
I1 von unten nach oben
I2 von rechts nach links
I3 von rechts nach links
I4 von oben nach unten
I7 je nach Größe der anderen Widerstände; ich lege hier mal die Richtung von oben nach unten fest
Unter Berücksichtigung der hier gemachten Festlegungen lauten die Knotengleichungen:
und die Maschengleichungen
-I_2\cdot R_2=0)
+I_3\cdot R_3=0)
Dieses System aus 6 Gleichungen mit 6 Unbekannten kannst Du jetzt z.B mit dem Gauß-Algorithmus lösen.
Da Du Deine Frage sehr allgemein gestellt hast, konntest Du auch nur eine sehr allgemeine Antwort erhalten. Sollte es sich aber um eine Aufgabe mit ganz konkreten Widerstandswerten handeln, solltest Du sie nennen. Möglicherweise ist die Aufgabe nämlich dann auch ganz einfach zu lösen. Da es sich um eine Brückenschaltung handelt, sollte man im konkreten Fall zuallererst überprüfen, ob es sich um eine abgeglichene Brücke handelt. Für den Fall der abgeglichenen Brücke lässt sich der Widerstand R7 durch jeden beliebigen anderen Widerstand ersetzen, z.B. durch den Widerstand Null oder durch eine unendlich hohen Widerstand. Das vereinfacht die Rechnung ganz erheblich und beschränkt die Schreibarbeit auf 3 oder 4 Zeilen.
|
|
|
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
| isi1 Verfasst am: 21. Jun 2014 14:27 Titel: |
|
|
| ineke hat Folgendes geschrieben: | | Kann mir bitte bitte jemand helfen, wie ich bei dem Chaos die Gleichungen richtig aufstellen? |
Versuchen wir es mal, ineke.
1. Der Spannung eine Richtung geben
2. die Kreisströme einzeichnen
3. die Matrix gemäß dem obigen Link aufstellen
4. Matrix lösen
5. Spezielle Werte daraus berechnen
| Code: | ik0 ik4 ik6 =
R2+R3 -R3 -R2 -U
-R3 R3+R4+R5+R7 -R7 0
-R2 -R7 R1+R2+R7+R6 0 |
Das ist die ganze nötige Schreibarbeit für die Gleichungen.
Falls unbekannt:
Die Matrix ist nur eine abgekürzte Schreibweise für folgende Gleichungen:
(R2+R3)ik0 -R3*ik4 -R2*ik6 = -U
-R3*ik0 +(R3+R4+R5+R7)ik4 -R7*ik6 = 0
-R2*ik0 -R7*ik4 +(R1+R2+R7+R6)ik6 = 0
Lösung ik0 = .... , ik4 = .... und ik6 = ....
Es ist zwar nicht schwer, diese Gleichungen zu lösen, aber viel Schreibarbeit.
Leichter gehts, wenn Du die Werte der R1...R7 herausrückst.
Vermutlich willst Du die Spannung UAB wissen?
Die wäre zu rechnen mit UAB = (ik6-ik4)*R7
Hilft Dir das weiter?
Edit isi: Aha, GvC war, wie schon oft, schneller. Na gut, hast gleich zwei mögliche Wege.
| Beschreibung: |
|
| Dateigröße: |
27.05 KB |
| Angeschaut: |
2407 mal |
|
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
|
ineke
Anmeldungsdatum: 20.06.2014
Beiträge: 11
|
| ineke Verfasst am: 21. Jun 2014 14:40 Titel: |
|
|
Vielen, lieben Dank euch beiden  .
Das hat mir sehr geholfen!!
|
|
|
ineke
Anmeldungsdatum: 20.06.2014
Beiträge: 11
|
| ineke Verfasst am: 21. Jun 2014 14:49 Titel: |
|
|
Und noch was, es ist bei dieser Aufgabe so, dass wird 6 Spannungen und 7 Widerstände bestimmt haben.
Daraufhin sollen wir nun die Maschenregel überprüfen und uns überlegen, wie wir die nicht gemessene Spannung U7 über ein Gleichungssystem eliminieren können.
Die Knotenregel sollen wir überprüfen, indem wir die zu-und abfließenden Ströme in Knoten A berechnen.
|
|
|
ineke
Anmeldungsdatum: 20.06.2014
Beiträge: 11
|
| ineke Verfasst am: 21. Jun 2014 15:18 Titel: |
|
|
|
dann kann ich doch alles so rechnen, wie GvC es aufgeschrieben hat, nur, dass ich für R7 und I7 überall null einsetze.. richtig?
|
|
|
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
| isi1 Verfasst am: 21. Jun 2014 16:44 Titel: |
|
|
| ineke hat Folgendes geschrieben: | | dann kann ich doch alles so rechnen, wie GvC es aufgeschrieben hat, nur, dass ich für R7 und I7 überall null einsetze.. richtig? |
Nee, ineke, so einfach gerade auch wieder nicht.
Du musst die bekannten Werte in die Gleichungen (oder meine Matrix) einsetzen und dann nach U7 (UAB) auflösen.
Ich habe in meinem Taschenrechner noch die Gleichungen für ik6 und ik4. Wenn Du die R1...R7 rausrückst, kann ich sie einsetzen.
Oder Du berechnest aus den 6 Spannungen gleich die U7.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
|
ineke
Anmeldungsdatum: 20.06.2014
Beiträge: 11
|
| ineke Verfasst am: 22. Jun 2014 10:47 Titel: |
|
|
Hey isi1,
das Problem ist, dass ich ein wissenschaftliches Protokoll schreiben muss und dafür die genaue Rechnung brauche bzgl der Aufgabenstellung, die ich gestern noch dargelegt habe.
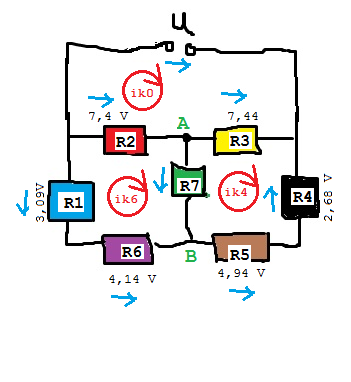
Ich habe dafür folgende Werte:
U1 3,09V
U2 7,4 V
U3 7,44 V
U4 2,68 V
U5 4,94 V
U6 4,14 V
Und die Widerstände (alle in KILOOHM):
R1 0,727
R2 1,904
R3 2,51
R4 0,81
R5 1,50
R6 0,99
R7 0,20
Ich hoffe sehr, dass du mir da hinsichtlich der Rechnungen (siehe Aufgabenstellung (gestern)) helfen kannst.
|
|
|
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
| isi1 Verfasst am: 22. Jun 2014 12:22 Titel: |
|
|
Wenn ich die Widerstandswerte in den TR eingebe, ineke, sagt er:
ik0 = -0,474887 * U = - 7,05 mA
ik4 = -0,247387 * U = - 3,67 mA
ik6 = -0,249584 * U = - 3,71 mA
Da Du die Widerstände in kOhm hast, sind die Ströme in mA
Daraus errechnet sich I7 = ik6-ik4 = -0,002197 * U = - 0,0326 mA
und U7 = I7*R7 = -0,000439 * U = -0,000439 * 14,845 V = -6,5 mV
Bei den Spannungen kann man nicht rechnen, solange die Spannungspfeile nicht bekannt sind, also zeichne ich mal die Spannungen ein.
U = U2+U3 = 14,84 V oder U = U1+U4+U5+U6 = 14,85 V
Daraus oben blau die Werte mit U=14,845
U7 = U2 - (U1+U6) = -0,17 V oder U7 = U3 - (U4+U5) = -0,18 V
Das sind allerdings große Abweichungen.
Sehen wir mal dei Brückenwiderstände an:
R2/R3 = 0,759
(R1+R6)/(R5+R4) = 0,743
Leerlaufspannung UABo = 0,227 V
Innenwiderstand hierzu Ri = 2,106 kOhm
I7 = UABo / (Ri+R7) = 0,098 mA
U7 = R7 * I7 = 19,7 mV
Aha, das deutet doch noch auf einen Rechenfehler.
Mags mal bitte nachrechnen, ineke, ich erzeuge zwischenzeitlich die explizite Auflösung der Matrix.
| Beschreibung: |
|
| Dateigröße: |
29.58 KB |
| Angeschaut: |
2352 mal |
|
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
|
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
| isi1 Verfasst am: 22. Jun 2014 12:41 Titel: |
|
|
Lösung des Gleichungssystems | Code: |
ik0 ik4 ik6 =
R2+R3 -R3 -R2 -U
-R3 R3+R4+R5+R7 -R7 0
-R2 -R7 R1+R2+R7+R6 0
Gleichungssystem, Widerstandswerte eingesetzt (für U setze ich 14,845 V ein)
Gleichungssystem:
4,414 -2,51 -1,904 -14,845
-2,51 5,02 -0,2 0
-1,904 -0,2 3,821 0
Umformen und sortieren (Variablen alphabetisch links, Konstanten rechts):
Stelle die Koeffizientenmatrix auf. Reihenfolge der Variablen: , , , Konstante
2207 251 238 2969
———— - ——— - ——— - ————
500 100 125 200
251 251 1
- ——— ——— - — 0
100 50 5
238 1 3821
- ——— - — ———— 0
125 5 1000
Durch Multiplikation der 1. Zeile mit 500/2207 wird das Diagonalelement zu 1 gemacht:
1255 952 14845
1 - ———— - ———— - —————
2207 2207 4414
251 251 1
- ——— ——— - — 0
100 50 5
238 1 3821
- ——— - — ———— 0
125 5 1000
Mit der 1. Zeile werden alle anderen Zeilen in der 1. Spalte auf 0 gebracht.
Zur 2. Zeile wird das 251/100fache der 1. Zeile addiert:
1255 952 14845
1 - ———— - ———— - —————
2207 2207 4414
792909 70773 745219
0 —————— - ————— - ——————
220700 55175 88280
238 1 3821
- ——— - — ———— 0
125 5 1000
Zur 3. Zeile wird das 238/125fache der 1. Zeile addiert:
1255 952 14845
1 - ———— - ———— - —————
2207 2207 4414
792909 70773 745219
0 —————— - ————— - ——————
220700 55175 88280
70773 6620339 353311
0 - ————— ——————— - ——————
55175 2207000 55175
Durch Multiplikation der 2. Zeile mit 220700/792909 wird das Diagonalelement zu 1 gemacht:
1255 952 14845
1 - ———— - ———— - —————
2207 2207 4414
94364 14845
0 1 - —————— - —————
264303 6318
70773 6620339 353311
0 - ————— ——————— - ——————
55175 2207000 55175
Mit der 2. Zeile werden alle anderen Zeilen in der 2. Spalte auf 0 gebracht.
Zur 1. Zeile wird das 1255/2207fache der 2. Zeile addiert:
668 14845
1 0 - ———— - —————
1053 3159
94364 14845
0 1 - —————— - —————
264303 6318
70773 6620339 353311
0 - ————— ——————— - ——————
55175 2207000 55175
Zur 3. Zeile wird das 70773/55175fache der 2. Zeile addiert:
668 14845
1 0 - ———— - —————
1053 3159
94364 14845
0 1 - —————— - —————
264303 6318
2045114513817662 495823
0 0 ———————————————— - ——————
804612502029375 52650
Durch Multiplikation der 3. Zeile mit 804612502029375/2045114513817662 wird das Diagonalelement zu 1 gemacht:
668 14845
1 0 - ———— - —————
1053 3159
94364 14845
0 1 - —————— - —————
264303 6318
24349693883893480
0 0 1 - —————————————————
6571977487335199
Mit der 3. Zeile werden alle anderen Zeilen in der 3. Spalte auf 0 gebracht.
Zur 1. Zeile wird das 668/1053fache der 3. Zeile addiert:
18371910493014176
1 0 0 - —————————————————
2606058520944591
94364 14845
0 1 - —————— - —————
264303 6318
24349693883893480
0 0 1 - —————————————————
6571977487335199
Zur 2. Zeile wird das 94364/264303fache der 3. Zeile addiert:
18371910493014176
1 0 0 - —————————————————
2606058520944591
4691857981160867
0 1 0 - ————————————————
1277579470228696
24349693883893480
0 0 1 - —————————————————
6571977487335199
Oder als Dezimalbruch
1 0 0 -7,049692225
0 1 0 -3,6724588102
0 0 1 -3,705078712
In der letzten Spalte stehen die Lösungen.
|
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
|
ineke
Anmeldungsdatum: 20.06.2014
Beiträge: 11
|
| ineke Verfasst am: 22. Jun 2014 12:47 Titel: |
|
|
Oh wow^^ Danke
Aber wenn ich ehrlich sein soll, habe ich das Gefühl, dass ich momentan ein Brett vor dem Kopf habe. Weil mir irgendwie nicht klar ist, wie ich mit den drei Lösungen sagen kann, ob das nun die Kirchhoffschen Regeln erfüllt oder nicht...
|
|
|
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
| isi1 Verfasst am: 22. Jun 2014 13:03 Titel: |
|
|
| ineke hat Folgendes geschrieben: | | ... wie ich mit den drei Lösungen sagen kann, ob das nun die Kirchhoffschen Regeln erfüllt oder nicht... |
Na ja, die gemessenen Spannungen widersprechen natürlich - wenn man es ganz genau nimmt - den Kirchhoffschen Gesetzen, da die Summe der Spannungen in einem geschlossenen Kreis nicht = 0 ist. Hat man zusätzlich Toleranzen der Messwerte, sieht es schon wieder besser aus.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
|
ineke
Anmeldungsdatum: 20.06.2014
Beiträge: 11
|
| ineke Verfasst am: 22. Jun 2014 13:42 Titel: |
|
|
|
Ja aber auch bei den Knotengleichungen kommt überall nicht null raus ... oh man
|
|
|
|
Registrieren
Login
FAQ
Suchen
