Kommutator [x,H] berechnen

escapado · Anmeldungsdatum: 08.05.2013 Beiträge: 49

Hallo, meine Aufgabe lautet wie folgt:
Betrachten Sie ein Teilchen im Potential mit Hamiltonoperator

Berechnen Sie dafür die Kommutatoren [x,H] und [p,H]

Also zunächst bin ich ein klein wenig verunsichert weil deine keine Hütchen über den Operatoren sind aber ich denke mal die soll ich mir dazu denken sonst steht da ja nur die Hamiltonfunktion. Ich habe mir nun folgendes gedacht:

Kann das sein oder mache ich einen schlimmen Fehler? Der 1 und 3, sowie der 2 und 4. Term haben sich ja weg und die zweifache Ableitung von x nach x ist doch null oder nicht?

Wenn ich nämlich im Schwabl schaue, dann steht da was ganz anderes und deshalb bin ich etwas verunsichert. Wenn das geklärt ist denke ich ,dass ich den anderen Kommutator richtig bestimmen kann. smile

adsadsd · Gast

Du muss die Produktregel für jede Ableitung einzeln ausführen.

TomS · Moderator Anmeldungsdatum: 20.03.2009 Beiträge: 18016

Also zunächst mal solltest du dich entscheiden, ob du in der Orstdarstellung

oder darstellungsfrei arbeitest.

Wenn du die Orstdarstellung nutzt, dann ist x immer eine (reelle) Zahl und kommutiert mit jeder Funktion von x. D.h. es ist sicher

Für den Kommutator von p mit einer Funktion von p kannst du genauso argumentieren (Kommutatoren sind darstellungsunabhängig, d.h. für p kannst du in der p-Darstellung mit p als reeller Zahl argumentieren). Außerdem kannst du argumentieren, dass in der Ortsdarstellung die Ableitungen vertauschen

Lange Rede - kurzer Sinn, es ist sicher

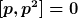
Die eigtl. Problematik liegt in den gemischten Termen und in der Bedeutung der Ableitung. Das kannst du umgehen, wenn du darstellungsfrei arbeitest.

Wenn du allerdings in der Ortsdarstellung arbeitest, musst du dir darüber im klaren sein, dass die Operatoren nach rechts immer auf eine Wellenfunktion wirken müssen. In deinem Fall hast du also z.B.

Außerdem musst du bei der Ableitung die Produktregel berücksichtigen.

Dabei ist

Wie du richtig erkannt hast ist der erste Term Null, und der letzte Term fällt im Kommutator weg. Aber der zweite Term bleibt stehen.

escapado · Anmeldungsdatum: 08.05.2013 Beiträge: 49

Ahhh, da lag mein Fehler! Danke euch beiden! TomS, sag mal in welchem Buch findet man eine darstellungsfreie Beschreibung? Wir haben bisher immer in der Ortsdarstellung gerechnet aber leider wurde bei uns das ganze auch ziemlich lari-fari-mäßig eingeführt. Edit: Insbesondere würde mich eine etwas mathematisch rigorosere Beschreibung freuen.

TomS · Moderator Anmeldungsdatum: 20.03.2009 Beiträge: 18016

Sakurai ist eine gute Wahl. Und evtl. Ballantine, wobei ich den nicht aus eigener Erfahrung kenne.

Feucht von Lipwig · Anmeldungsdatum: 19.09.2013 Beiträge: 122