FAQ - Zeitdilatation und Zwillingsparadoxon

TomS · Moderator Anmeldungsdatum: 20.03.2009 Beiträge: 18010

Im folgenden möchte ich kurz zusammenfassen, wie man die Zeitdilatation bzgl. der Eigenzeiten zweier Beobachter im Rahmen der speziellen Relativitätstheorie definiert. Dabei lasse ich beliebige (auch nicht-geradlinige und nicht-konstante) Geschwindigkeiten zu. Die allgemeine Form der Zeitdilatation folgt daher auch nicht aus der Lorentztransformation, die ja nur für Inertialsysteme gilt. Die Betrachtung löst auch das bekannte Zwillingsparadoxon.

Man betrachtet die Weltlinien der beiden Beobachter i=1,2 in der vierdimensionalen Raumzeit, die einen gemeinsamen Start- sowie Endpunkt haben, ansonsten jedoch beliebig sind. Die beiden Zwillinge vergleichen ihre Uhren am Start und am Ziel der Reise. Die Eigenzeit tau entlang einer derartigen Kurve C, also die Zeit, die ein Beobachter auf einer mitbewegten Uhr misst und die für ihn vergeht, lautet

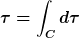
Zur Berechnung des Kurvenintegrals benötigt man die "vierdimensionale Länge" im Minkowski-Raum, d.h.

wobei der Punkt die Ableitung nach einer Koordinatenzeit in einem beliebigen Inertialsystem bedeutet. Geschickterweise wählt man ein gemeinsames Koordinatensystem für beide Beobachter, so dass man wie folgt zusammenfassen kann:

Hier bedeutet t jeweils die Koordinatenzeit und v(t) die Geschwindigkeit des jeweiligen Beobachters im gewählten Koordinatensystem.

Zuletzt betrachtet man den Spezialfall, dass der erste Beobachter (Zwilling) in einem Inertialsystem ruht. Dann kann man dessen Ruhesystem als Bezugssystem verwenden, d.h. die Koordinatenzeit t sowie die Eigenzeit tau des ersten Zwillings identifizieren. Man erhält

Natürlich kann v(t) des zweiten Beobachters (Zwillings) nicht vektoriell konstant sein, denn sonst könnte er nicht umkehren und zum ersten Zwilling an einem gemeinsamen Endpunkt zurückkehren. Man kann sich jedoch statt eines geraden Hin- und Rückfluges mit Verzögerung, Umkehren und Beschleunigen auch eine Kreisbahn mit konstantem Geschwindigkeitsbetrag vorstellen. In diesem Spezialfall folgt für das Integral

Man erhält die bekannte Formel mittels des Quotienten

TomS · Moderator Anmeldungsdatum: 20.03.2009 Beiträge: 18010

Kurze Zusammenfassung der Erkenntnisse und worum es mir ging:

1) Eigenzeit ist eine sowohl messbare als auch berechenbare Größe
2) Die Definition von Eigenzeit erfolgt koordinatenfrei (Linienintegral)
3) Diese Definition ist auf die ART verallgemeinerbar (gilt nicht für die Koordinatendarstellung)
4) Es ist für Zwillingsparadoxon nicht notwendig, mit Inertialsystemen zu argumentieren; man kann auch zwei Beobachter in zwei nicht-Inertialsystemen betrachten
5) Die Zeitdilatation ist kein Spezialfall der Lorentztransformation; letztere wird nicht zur Definition benötigt (in der ART existiert keine globale Lorentzinvarianz)
6) Der Ansatz fokussiert auf physikalisch messbare, invariante Größen, anstelle von koordinatenabhängigen Hilfsgrößen

Ich halte (6) für sehr wichtig. Die RT wird häufig mittels Lorentztransformationen eingeführt; es entsteht der Eindruck, es ginge nur um Umrechnungen zwischen Koordinatensystemen. Das ist falsch; viel wichtiger für dir Physik sind invariante, koordinatenfreie Größen (Eigenzeit, invariante Ruhemasse, ...) Also sollte man wo immer möglich diese in den Mittelpunkt der Diskussion stellen.

TomS · Moderator Anmeldungsdatum: 20.03.2009 Beiträge: 18010

Im folgenden möchte ich kurz zeigen, wie die obige Herleitung der kinematischen Zeitdilatation im Rahmen der SRT auf die ART erweitert werden kann. Dabei zeigt sich, dass kinematische und gravitative Effekte miteinander verwoben sind und lediglich in Spezialfällen - die jedoch für bestimmte Probleme zumindest näherungsweise zutreffen - separiert werden können.

Wir gehen aus von der Eigenzeit tau eines Beobachters entlang seiner Weltlinie C. Dafür hatten wir den Ausdruck

abgeleitet.

Diese Formel gilt allgemein für die ART, wenn zur Berechnung des Skalarproduktes eine Metrik g verwendet wird, die die nicht-triviale Geometrie der Raumzeit beschreibt:

In der ursprünglichen Darstellung ist die Formel allgemeingültig, d.h. sie gilt für beliebige Raumzeiten und sie ist koordinatensystemunabhängig formulierbar (die Eigenzeit als "verallgemeinerte Länge" der Kurve C hängt nicht vom verwendeten Koordinatensystem ab). Um nun konkrete Berechnungen durchzuführen, muss i) eine konkrete Raumzeit betrachtet werden, und ii) diese Raumzeit muss in einem konkreten Koordinatensystem dargestellt werden, d.h. die Metrik g gilt bzgl. dieser Koordinaten. Die oben eingeführte Koordinatenzeit t ist demnach eine (ggf. unbeobachtbare, unphysikalische) Hilfsgröße, die aus den Endergebnissen eliminiert werden kann.

In vielen Fällen kann die Metrik auf Diagonalform gebracht werden, wobei die Diagonalelemente (für 0, sowie i=1,2,3) noch Funktionen der Koordinaten sein können. Das Integral lauten dann

In dieser Form können z.B. die Schwarzschildgeometrie für das Gravitationsfeld einer sphärisch symmetrischen Massenverteilung sowie die FRW-Geometrie für ein homogenes und isotropes Universum dargestellt werden. Sowohl die Metrik g als auch die räumliche Geschwindigkeit können dabei (entlang der betrachteten Bahnkurve C) zeitabhängig sein. Erstere gilt z.B. für den Fall eines expandierenden Universums.

Zuletzt möchte ich auf einige Spezialfälle eingehen.

1) Die spezielle Formel für die SRT erhält man mittels der flachen Minkowskimetrik

zurück.

2) Im Falle eines bzgl. des gewählten Koordinatensystems ruhenden Beobachters ist dessen Geschwindigkeit Null; es folgt

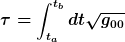
Dies gilt z.B. für einen ortsfesten Beobachter in der Schwarzschildgeometrie oder einen "mitbewegten Beobachter" in einem expandierenden FRW-Universum.

3) Wenn die Raumzeit außerdem statisch ist, d.h. wenn die Metrik nicht zeitabhängig ist, dann folgt sofort

d.h. die Eigenzeit ist zur Koordinatenzeit proportional. Der Proportionalitätsfaktor enthält die 00-Komponente der Metrik, d.h. aus dieser ist die tatsächliche Eigenzeit direkt ablesbar. Diese Spezialisierung gilt wieder für die Schwarzschildgeometrie.

TomS · Moderator Anmeldungsdatum: 20.03.2009 Beiträge: 18010

Speziell für die Schwarzschildmetrik gilt

Damit folgen für eine Schar von Beobachtern mit jeweils konstanten Abständen die Eigenzeiten

und für zwei deratige Beobachter das Verhältnis der Eigenzeiten (wobei die Schwarzschild-Koordinatenzeit t herausfällt)

Für eine Schar von äquatorial kreisenden (nicht-geodätischen) Beobachtern mit jeweils konstanten Abständen und konstanten Geschwindigkeiten folgen die Eigenzeiten

Für einen bei Radius r ruhenden sowie einen bei identischem Radius kreisenden Beobachter gilt

TomS · Moderator Anmeldungsdatum: 20.03.2009 Beiträge: 18010

Anbei nochmal eine kurze Bemerkung zur Rolle der Beschleunigung zur Auflösung des sogenannten "Paradoxons". Aus den o.g. Formeln geht hervor, dass die Beschleunigung bei der Berechnung der Zeitdilatation keine Rolle spielt (sie geht nicht in die Integrale ein).

Man vergleiche zwei kreisförmige Bahnkurven, die sich an einem Punkt (= gemeinsamer Start- und Zielpunkt) berühren. Die beiden Bahnkurven werden periodisch mit konstantem Geschwindigkeitsbetrag durchlaufen. Es gilt die o.g. Beziehung

Setzen wir

Dann ist

Nun führen wir eine variable Geschwindigkeit

ein. Der strikt positive, variable Anteil entspricht einer Beschleunigung des ersten Zwillings. Insgs. ist dessen Geschwindigkeit jedoch nach wie vor kleiner als die des zweiten Zwillings.

Damit können wir das Integral zur Berechnung der Eigenzeit des ersten Zwillings wie folgt abschätzen:

Und damit gilt weiterhin

Nun kann die Beschleunigung über den variablen Anteil beliebig, d.h. betragsmäßig unbeschränkt groß werden, ohne dass diese Ungleichung verletzt wird. D.h. bei der Berechnung dominiert weiterhin der Effekt der größeren Geschwindigkeit über den der beschleunigten Bewegung.

Die Zeitdilatation "misst" demnach nicht die Beschleunigungen, sondern die (Beträge der) Geschwindigkeiten.

TomS · Moderator Anmeldungsdatum: 20.03.2009 Beiträge: 18010

Ich möchte den Thread um einen weiteren Aspekt ergänzen, nämlich um die Zeitdilatation in einem (homogen und isotrop) expandierenden Universum. Man liest die Eigenzeit tau entlang einer Weltlinie C wiederum direkt an der Metrik (hier speziell Friedmann-Robertson-Walker) bzw. dem Linienelement ab.

Für eine (aus Sicht des mitbewegten Koordinatensystems) rein radiale Bewegung gilt

Damit ist klar, dass die Zeitdilatation für eine "bestimmte Reise" abhängig davon ist, "zu welcher Zeit t" die Reise durchgeführt wird. Identische Zeitdilatationen für verschiedene Zeiten erhält man speziell dann, wenn nicht v sondern av entlang C übereinstimmt.