| Autor |
Nachricht |
mocx
Gast
|
 mocx Verfasst am: 05. März 2014 23:24 Titel: Herleitung elektrischer Felder von Kondensatoren mocx Verfasst am: 05. März 2014 23:24 Titel: Herleitung elektrischer Felder von Kondensatoren |
 |
|
Hallo 
Zum Verständnis, möchte ich die Formeln für elektrische Felder bei Kondensatoren herleiten.
Ich gehe von folgender Darstellung aus:
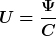
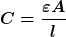
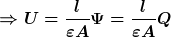
eingesetzt in 
Diese Darstellung nutz ich nun mit den jeweiligen Flächen für die elektrischen Felder.
Für einen Plattenkondensator seh ich immer:

Also genau die Ausgangsformel. Speichert der Plattenkondensator, die Energie im
gesamten Flächeninhalt? Oder nur an der Oberfläche?
Ein Kondensator als Hohlzylinder bereitet mir auch Probleme.
Beim Vollzylinder nimm ich für A die Mantelfläche und es ergibt sich:
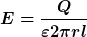
Muss ich dann beim Hohlzylinder die "Wanddicke" für die Mantelfläche nehmen? Also:  l} )
Danke im Voraus  |
|
 |
stereo
Anmeldungsdatum: 27.10.2008
Beiträge: 402
|
 stereo Verfasst am: 06. März 2014 08:05 Titel: Re: Herleitung elektrischer Felder von Kondensatoren stereo Verfasst am: 06. März 2014 08:05 Titel: Re: Herleitung elektrischer Felder von Kondensatoren |
 |
|
Hallo,
also die Herleitung sieht m.E. anders aus. Hierfür benötigst du die Maxwell-Gleichungen oder du berechnest das elektrische Potential zweier Platten.
Die lineare Beziehung
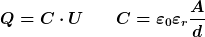
gilt gerade für den Plattenkondensator, sodass du etwas in deine "Herleitung" steckst, was du eigentlich berechnen willst.
Wenn du wissen willst, wo die Energie gespeichert wird, dann musst du wissen warum überhaupt Energie gespeichert wird. Weißt du das? Des Weiteren gibt es bei Kondensatoren mit Dielektrika zwei Anteile. |
|
 |
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3419
|
 ML Verfasst am: 06. März 2014 11:40 Titel: Re: Herleitung elektrischer Felder von Kondensatoren ML Verfasst am: 06. März 2014 11:40 Titel: Re: Herleitung elektrischer Felder von Kondensatoren |
 |
|
Hallo,
| mocx hat Folgendes geschrieben: |
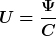
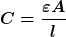
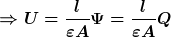
|
Was willst Du denn mit dem magnetischen Fluß 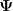 ? ?
| Zitat: |
Speichert der Plattenkondensator, die Energie im
gesamten Flächeninhalt? Oder nur an der Oberfläche?
|
Weder noch. Die Energie befindet sich im elektrischen Feld. Energiedichte (d. h. Energie geteilt durch Volumen)
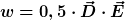 . .
| Zitat: |
Beim Vollzylinder nimm ich für A die Mantelfläche und es ergibt sich:
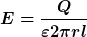
Muss ich dann beim Hohlzylinder die "Wanddicke" für die Mantelfläche nehmen? Also:  l} )
|
Bei Deiner Formel stimmt etwas nicht. Das E-Feld beim Zylinderkondensator hängt vom Radius ab.
Als Ansatz kannst Du von einer gegebenen Ladung ausgehen und den Satz von Gauß anwenden.
Viele Grüße
Michael |
|
 |
mocx
Gast
|
 mocx Verfasst am: 06. März 2014 12:29 Titel: mocx Verfasst am: 06. März 2014 12:29 Titel: |
 |
|
Danke erstmal :)
An Stereo:
Ich hab es so verstanden, dass die Metallplatten (Beim Plattenkondensator), negative und positive Ladungen speichern, jeweils auf entgegengesetzten Platten - und durch deren Anziehungswirkung auf der gegenüberliegenden Platte ein elektrisches Feld entsteht.
An ML:
Ich hab mich sehr missverständlich ausgedrückt.
Ich frage mich einfach, ob ich die gesamte Plattenfläche betrachte (oder nur den Anteil der Fläche, der jeweils zur gegenüberliegenden Platte schaut (Plattenkondensator)
Zum Hohlzylinder:
Den Satz von Gauß haben wir bisher leider nicht behandelt. Wie kann ich da noch vorgehen? |
|
 |
stereo
Anmeldungsdatum: 27.10.2008
Beiträge: 402
|
 stereo Verfasst am: 06. März 2014 13:07 Titel: stereo Verfasst am: 06. März 2014 13:07 Titel: |
 |
|
| mocx hat Folgendes geschrieben: |
An Stereo:
Ich hab es so verstanden, dass die Metallplatten (Beim Plattenkondensator), negative und positive Ladungen speichern, jeweils auf entgegengesetzten Platten - und durch deren Anziehungswirkung auf der gegenüberliegenden Platte ein elektrisches Feld entsteht.
|
Für den Fall, dass der Zwischenraum leer ist, steckt die gespeicherte Energie wirklich im elektrischem Feld. Dieses wird auch durch die freien Ladungsträgern in den Platten erzeugt.
Wenn sich ein Dielektrikum zwischen den Platten befindet, dann wird ein Teil (meist der Größere) auch im Dielektrikum gespeichert. Stichwort: Verschiebungspolarisation. Wenn du das verstanden hast, dann weist du ob im gesammten Dielektrikum die Energie gespeichert wird oder nur am Rand. |
|
 |
mocx
Gast
|
 mocx Verfasst am: 06. März 2014 13:14 Titel: mocx Verfasst am: 06. März 2014 13:14 Titel: |
 |
|
|
Bisher dachte ich, dass ich diesen Begriff kenne. Kann das aber auf meine eigentliche Problemstellung nicht zurückführen. Handelt es sich dabei nicht um die Verschiebung der Ladungsschwerpunkte? |
|
 |
stereo
Anmeldungsdatum: 27.10.2008
Beiträge: 402
|
 stereo Verfasst am: 06. März 2014 13:19 Titel: stereo Verfasst am: 06. März 2014 13:19 Titel: |
 |
|
|
Ja, genau. Sie werden aufgrund des elektrischen Feldes verschoben. Welche Kraft wirkt entgegen, sodass in völliger Analogie zur Feder Energie gespeichert wird? |
|
 |
mocx
Gast
|
 mocx Verfasst am: 06. März 2014 13:24 Titel: mocx Verfasst am: 06. März 2014 13:24 Titel: |
 |
|
|
Coulombkraft <-> Potentielle Energie? |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 06. März 2014 13:33 Titel: GvC Verfasst am: 06. März 2014 13:33 Titel: |
 |
|
| stereo hat Folgendes geschrieben: | | Für den Fall, dass der Zwischenraum leer ist, steckt die gespeicherte Energie wirklich im elektrischem Feld. |
Das gilt auch für den Fall, dass der Zwischenraum (zwischen den Elektroden) nicht leer ist.
Ich fürchte, dass bei mocx ein grundsätzliches Missverständnis existiert. Auf die Energie kam er nämlich im Zusammenhang mit der Gleichung
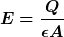
Dabei steht das Symbol E aber nicht für die Energie, sondern für die elektrische Feldstärke. Und das ist etwas ganz Anderes. |
|
 |
mocx
Gast
|
 mocx Verfasst am: 06. März 2014 13:43 Titel: mocx Verfasst am: 06. März 2014 13:43 Titel: |
 |
|
Ich hab mich wirklich sehr missverständlich in diesem Thread ausgedrückt. Es ging mir darum, die Formeln für die Elektrische Feldstärke für jeweils verschiedene geometrische Körper (Kondensatoren) herzuleiten. Die Energiespeicherung hatte ich nur nebenbei erwähnt.
Die Frage, ob die Fläche  (die soweit ich weiß die Fläche der Äquipotenzialfläche ist), nun beim Plattenkondensator dem gesamten Flächeninhalt (die soweit ich weiß die Fläche der Äquipotenzialfläche ist), nun beim Plattenkondensator dem gesamten Flächeninhalt  ) entspricht oder nur der Plattenoberfläche die zur anderen Platte hinguckt, also: entspricht oder nur der Plattenoberfläche die zur anderen Platte hinguckt, also: 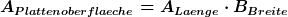 . .
Das ich die Frage nicht beantworten kann, liegt sicherlich daran, dass ich ein tieferes Verständnis für Felder und Kondensatoren brauche. |
|
 |
stereo
Anmeldungsdatum: 27.10.2008
Beiträge: 402
|
 stereo Verfasst am: 06. März 2014 16:05 Titel: stereo Verfasst am: 06. März 2014 16:05 Titel: |
 |
|
| GvC hat Folgendes geschrieben: | | stereo hat Folgendes geschrieben: | | Für den Fall, dass der Zwischenraum leer ist, steckt die gespeicherte Energie wirklich im elektrischem Feld. |
Das gilt auch für den Fall, dass der Zwischenraum (zwischen den Elektroden) nicht leer ist. |
Aber dann ist nicht die gesamte Energie im Feld gespeichert. |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 06. März 2014 16:48 Titel: GvC Verfasst am: 06. März 2014 16:48 Titel: |
 |
|
@mocx
Um Deinem Verständnis ein bisschen auf die Sprünge zu helfen, stelle Dir vor, dass zwischen den Platten eines Plattenkondensators ein Fluss von der einen Platte zur anderen fließt. Tatsächlich fließt da gar nichts, es sieht in der grafischen Darstellung nur so aus. Denn wenn Du von der positiven zur negativen Platte eine oder mehrere Linien ziehst (sog. Feldlinien) und diese Linien von Plus nach Minus noch mit Pfeilspitzen versiehst, dann sieht das tatsächlich so aus, als würde da etwas fließen. Tatsächlich bezeichnet man das, was so aussieht wie ein Fluss, als dielektrischen Fluss und bezeichnet ihn im Gegensatz zur Behauptung von ML zuweilen mit 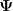 . (Nebenbei: Nach Gaußschem Flusssatz ist dieser dielektrische Fluss . (Nebenbei: Nach Gaußschem Flusssatz ist dieser dielektrische Fluss 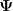 gleich dem Betrag der auf einer Platte gespeicherten Ladung Q, wobei die Ladungen auf beiden Platten ja entgegengesetzt gleich groß sind). Insofern war deine Ausgangsgleichung durchaus richtig gleich dem Betrag der auf einer Platte gespeicherten Ladung Q, wobei die Ladungen auf beiden Platten ja entgegengesetzt gleich groß sind). Insofern war deine Ausgangsgleichung durchaus richtig
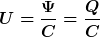
Diese Gleichung erinnert stark an das ohmsche Gesetz
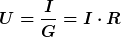
Es lässt sich also eine Analogie zwischen dielektrischem und ohmschem Fall insofern herstellen, als der Fluss 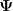 analog dem Strom I und der Kehrwert der Kapazität analog dem Widerstand R ist. Man bezeichnet den Kehrwert der Kapazität deshalb auch als dielektrischen Widerstand. analog dem Strom I und der Kehrwert der Kapazität analog dem Widerstand R ist. Man bezeichnet den Kehrwert der Kapazität deshalb auch als dielektrischen Widerstand.
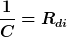
Wohlgemerkt, physikalisch hat der dielektrische Widerstand Rdi nichts, aber auch gar nichts mit dem ohmschen Widerstand R zu tun. Mathematisch aber erhält man mit dem dielektrischen Widerstand eine dem ohmschen Gesetz analoge Gesetzmäßigkeit
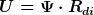
Die Vorstellung eines dielektrischen Widerstandes erleichtert auch die Berechnung von Reihen und Parallelschaltungen von Kapazitäten:
Reihenschaltung
im ohmschen Fall
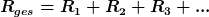
analog dazu im dielektrischen (kapazitiven Fall)
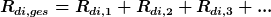
was mit der Definition Rdi=1/C gleichbedeutend ist mit
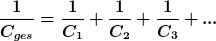
Parallelschaltung
im ohmschen Fall
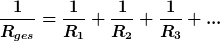
im dielektrischen Fall
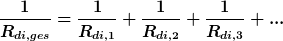
was gleichbedeutend ist mit
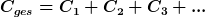
Genauso gut lässt sich diese Analogie anwenden auf die Spannungsteilerregel und die Strom- bzw. Flussteilerregel.
Die Analogie ist auch besonders hilfreich bei der Bestimmungsgleichung für die Kapazität. Im ohmschen Fall gilt ja
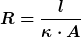
mit
l = Ausdehnung in Strom-(Fluss-)Richtung
A = die senkrecht zu l liegende durchströmte Fläche
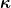 = ohmsche Leitfähigkeit = ohmsche Leitfähigkeit
Analog dazu
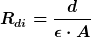
bzw.
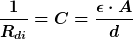
mit
d = Ausdehnung in Flussrichtung
A = die senkrecht zu d liegende vom dielektrischen Fluss durchsetzte Fläche
 = dielektrische Leitfähigkeit, wofür es einen speziellen Namen gibt, nämlich Permittivität = dielektrische Leitfähigkeit, wofür es einen speziellen Namen gibt, nämlich Permittivität
An dieser Stelle lässt sich Deine ursprüngliche Frage nach der Fläche auch anschaulich beantworten. Es ist die vom Fluss durchsetzte Fläche, also die zweidimensionale "Größe" der Kondenstorplatten A=a*b bei Platten der Länge a und Breite b.
Du siehst an dieser Stelle auch, dass sich die Kapazität eines Zylinderkondensators der Länge l nicht so einfach nach obiger Bestimmungsgleichung ermitteln lässt. Denn die vom Fluss durchsetzte Fläche wird auf dem Wege des Flusses vom Innenzylinder zum Außenzylinder immer größer. Du wüsstest also gar nicht, welchen Wert Du für die Fläche A einsetzen solltest.
Am Innenzylinder ist
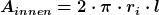
am Außenzylinder ist

und an jeder Stelle dazwischen allgemein
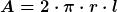
mit ri <= r <= ra
Wenn Du wissen willst, wie sich die Kapazität eines Zylinderkondensators dennoch bestimmen lässt, musst du das sagen. Die Frage nach der Fläche A in der Formel für die Kapazität ist hiermit jedenfalls erstmal beantwortet zusammen mit einer Verständnishilfe für Kondensatoren. |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 06. März 2014 16:51 Titel: GvC Verfasst am: 06. März 2014 16:51 Titel: |
 |
|
| stereo hat Folgendes geschrieben: | | GvC hat Folgendes geschrieben: | | stereo hat Folgendes geschrieben: | | Für den Fall, dass der Zwischenraum leer ist, steckt die gespeicherte Energie wirklich im elektrischem Feld. |
Das gilt auch für den Fall, dass der Zwischenraum (zwischen den Elektroden) nicht leer ist. |
Aber dann ist nicht die gesamte Energie im Feld gespeichert. |
Wo denn sonst?
Es gilt in jedem Fall
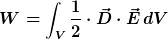 |
|
 |
stereo
Anmeldungsdatum: 27.10.2008
Beiträge: 402
|
 stereo Verfasst am: 06. März 2014 17:09 Titel: stereo Verfasst am: 06. März 2014 17:09 Titel: |
 |
|
Sie ist in den induzierten Dipolen innerhalb des Dielektrikums gespeichert. Die Energiedichte im Feld ist gegeben durch
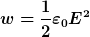
, wobei der Anteil durch die induzierten Dipole nicht enthalten ist. Der erste Summand der dielektrischen Verschiebung
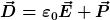
beschreibt das Feld im Vakuum. Die Polarisation ist vom Dielektrikum abhängig. |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 06. März 2014 17:26 Titel: GvC Verfasst am: 06. März 2014 17:26 Titel: |
 |
|
| stereo hat Folgendes geschrieben: | Sie ist in den induzierten Dipolen innerhalb des Dielektrikums gespeichert. Die Energiedichte im Feld ist gegeben durch
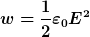
, wobei der Anteil durch die induzierten Dipole nicht enthalten ist. Der erste Summand der dielektrischen Verschiebung
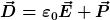
beschreibt das Feld im Vakuum. Die Polarisation ist vom Dielektrikum abhängig. |
Das ist richtig, wenn Du die Energiedichte so definierst wie du es tust. Allerdings ist die in den ausgerichteten Dipole gespeicherte Energie ebenfalls Feldenergie, oder wie würdest Du die bezeichnen.
Tatsächlich lässt sich Deine zweite Gleichung praktischerweise anders schreiben, nämlich
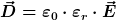
wobei E die Feldstärke ist, die sich aus der Beziehung
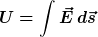
ergibt. Damit ist die Energiedichte
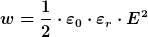
Da E eindeutig eine Feldgröße ist, lässt sich sehr guten Gewissens sagen, dass die Energie im Feld gespeichert ist. |
|
 |
stereo
Anmeldungsdatum: 27.10.2008
Beiträge: 402
|
 stereo Verfasst am: 06. März 2014 17:37 Titel: stereo Verfasst am: 06. März 2014 17:37 Titel: |
 |
|
| GvC hat Folgendes geschrieben: |
Das ist richtig, wenn Du die Energiedichte so definierst wie du es tust. Allerdings ist die in den ausgerichteten Dipole gespeicherte Energie ebenfalls Feldenergie, oder wie würdest Du die bezeichnen.
|
Sie steckt aber in der Coulombkraft der verschiedenen Ladungsschwerpunkte der Atome. Des Wegen ist eine Trennung m.E. sinnvoll.
| GvC hat Folgendes geschrieben: |
Tatsächlich lässt sich Deine zweite Gleichung praktischerweise anders schreiben, nämlich
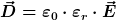
|
Für lineare, isotrope Dielektrika ist das schon der Fall. Das vereinfacht natürlich vieles  Aber das passt dann auch super in den Fall der Verschiebungspolarisation. Aber das passt dann auch super in den Fall der Verschiebungspolarisation.
| GvC hat Folgendes geschrieben: |
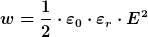
Da E eindeutig eine Feldgröße ist, lässt sich sehr guten Gewissens sagen, dass die Energie im Feld gespeichert ist. |
Also ich will keine Grundsatzdiskussion vom Zaun brechen. Du hast natürlich recht, aber eine Unterscheidung zwischen Energie der induzierten Dipole und Feldenergie des Vakuums halte ich für sinnvoll, weil das zwei unterschiedliche Mechanismen sind. Also es existieren zwei Felder.
edit: Warum brauchst du die Definition der Spannung? |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 06. März 2014 18:09 Titel: GvC Verfasst am: 06. März 2014 18:09 Titel: |
 |
|
| stereo hat Folgendes geschrieben: | | Also es existieren zwei Felder. |
Eben. Und aus diesem Grunde habe ich die Definition über die außen anliegende Spannung gebracht.
Nebenbei: Da es sich um zwei Felder handelt, die Du unterschieden wissen willst, wie willst Du die in beiden Feldern gespeicherten Energien denn nennen? Etwa nicht Feldenergie?
Ich bleibe dabei: Ein Kondensator speichert die Energie nicht auf den Platten, sondern dazwischen, also im elektrischen Feld. Diese Aussage sollte als Antwort auf die vom Threadersteller gestellte Frage ausreichend sein.
| mocx hat Folgendes geschrieben: | | Speichert der Plattenkondensator, die Energie im gesamten Flächeninhalt? Oder nur an der Oberfläche? |
(Wobei diese Formulierung weitere Fragen z.B. nach dem Unterschied zwischen Flächeninhalt und Oberfläche aufwirft, aber das war hier nicht das Thema) |
|
 |
mocx
Gast
|
 mocx Verfasst am: 07. März 2014 11:20 Titel: mocx Verfasst am: 07. März 2014 11:20 Titel: |
 |
|
Komisch, das mein Beitrag irgendwie nicht erschienen ist.
Erstmal einen großen Dank für deinen imposanten Beitrag, der so einige Missverständnisse bei mir aus dem Weg geräumt hab. Falls mir auffällt, dass ich noch einige Fragen hab, werde ich da nochmal drauf zurückkommen :)
Werde mich noch ein wenig mit "Kondensatornetzwerken" beschäftigen .. |
|
 |
|
















