| Autor |
Nachricht |
buell23
Anmeldungsdatum: 13.11.2006
Beiträge: 238
|
 buell23 Verfasst am: 20. Jan 2013 15:14 Titel: Erde stürzt in die Sonne |
 |
|
Hallo ihr
Ich habe da eine Frage und zwar heisst es, dass missgünstig gesinnte Außerirdische Rasse über die Technologie verfüge, die Erdrotation um die Sonne zu stoppen. Wie lange würde die Erde dann benötigen, um in die Sonne zu fallen.
R= 1,5*10^11
Masse der Sonne 2. 10^30
Ich habe es berechnet und komme auf ca. 80 Tage.
Aber die Beschleunigung bleibt ja nicht konstant, daher wie würde ich es auf die Weise der Integration berechnen?
Könnte mir diesbezüglich jemand einen Tipp geben, wie der Ansatz der Integration aussieht?
Danke vielmals
|
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5044
|
| DrStupid Verfasst am: 20. Jan 2013 17:39 Titel: Re: Erde stürzt in die Sonne |
|
|
| buell23 hat Folgendes geschrieben: | Aber die Beschleunigung bleibt ja nicht konstant, daher wie würde ich es auf die Weise der Integration berechnen?
Könnte mir diesbezüglich jemand einen Tipp geben, wie der Ansatz der Integration aussieht? |
Der Ansatz ergibt sich aus dem Newtonschen Gravitationsgesetz:
Mit dem dritten Keplersche Gesetz kommst Du aber auch ganz ohne Integration zum Ziel.
|
|
|
buell23
Anmeldungsdatum: 13.11.2006
Beiträge: 238
|
| buell23 Verfasst am: 20. Jan 2013 18:46 Titel: |
|
|
Hallo DrStupid
Jetzt habe ich etwas zu schnell gefragt.
Der Ansatz gleicht ja der 2. Ableitung des Weges = Beschleunigung.
Wenn ich dies richtig interpretiere, dann müsste die Rechnung folgend aussehen:
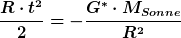
Irgendwo steckt nun ein Bock drinnen. Außerdem stört das Minus weges des Quadrats. Wo ist nun der Fehler?
Danke vorab
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18078
|
| TomS Verfasst am: 20. Jan 2013 19:22 Titel: |
|
|
Man kann auch mittels des Energiesatzes rechnen. Man bestimmt an jedem Punkt die Gesamtenergie als Summe der potentiellen und der kinetischen Energie und löst nach der Geschwindigkeit auf. Diese entspricht der ersten Ableitung dr/dt und damit erhält man eine DGL erster (statt zweiter) Ordnung. Lösung erfolgt mittels Trennung der Variablen und Integration.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
buell23
Anmeldungsdatum: 13.11.2006
Beiträge: 238
|
| buell23 Verfasst am: 20. Jan 2013 20:39 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | Man kann auch mittels des Energiesatzes rechnen. Man bestimmt an jedem Punkt die Gesamtenergie als Summe der potentiellen und der kinetischen Energie und löst nach der Geschwindigkeit auf. Diese entspricht der ersten Ableitung dr/dt und damit erhält man eine DGL erster (statt zweiter) Ordnung. Lösung erfolgt mittels Trennung der Variablen und Integration. |
Eigentlich müsste ich das nicht berechnen. Bin aber sehr interessiert zu einer entsprechenden Lösung zu kommen mittels allen 3 Möglichkeiten.
Ich habe aber noch nicht mit den Differentialgleichungen gearbeitet bzw. diese Gleichungen gelöst.
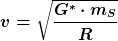
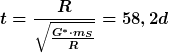
Wenn die Berechnung stimmt, würde ich gerne wissen wie ich nun die integrale Form fortsetzen kann. Was stimmt daran nicht?
|
|
|
##
Gast
|
| ## Verfasst am: 20. Jan 2013 22:09 Titel: |
|
|
| buell23 hat Folgendes geschrieben: | ...
Wenn die Berechnung stimmt, würde ich gerne wissen wie ich nun die integrale Form fortsetzen kann. Was stimmt daran nicht? |
Vielleicht ganz allgemein formuliert:
Alle Variablen auf jeweils eine Seite bringen, dabei das Differential möglichst nicht als Kehrwert schreiben.
(Wie kommt man nur auf so eine Aufgabe?).
|
|
|
D2
Anmeldungsdatum: 10.01.2012
Beiträge: 1723
|
| D2 Verfasst am: 20. Jan 2013 22:11 Titel: |
|
|
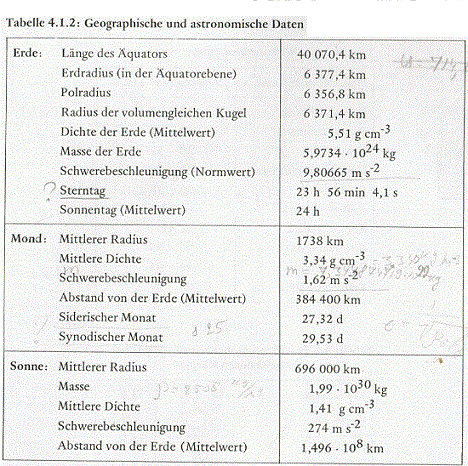
Ich komme auf 9St 10min 45 s
Rechnungsweg:
h =1,496*10E8km
Sonnenbeschleunigung a = 274m/s²
t= Wurzel(2*h/a)
Fallzeit t =33045s
http://de.wikipedia.org/wiki/Freier_Fall
| Beschreibung: |
|
| Dateigröße: |
74.88 KB |
| Angeschaut: |
8010 mal |
|
_________________
Lösungen gibt es immer, man muss nur darauf kommen. |
|
|
buell23
Anmeldungsdatum: 13.11.2006
Beiträge: 238
|
| buell23 Verfasst am: 20. Jan 2013 22:50 Titel: |
|
|
Ich habe deine Werte in deine t_Formel eingesetzt, komme aber nicht auf deine Lösung. Auch komme ich auf ein anderes a.
| ## hat Folgendes geschrieben: | | buell23 hat Folgendes geschrieben: | ...
Wenn die Berechnung stimmt, würde ich gerne wissen wie ich nun die integrale Form fortsetzen kann. Was stimmt daran nicht? |
Vielleicht ganz allgemein formuliert:
Alle Variablen auf jeweils eine Seite bringen, dabei das Differential möglichst nicht als Kehrwert schreiben.
(Wie kommt man nur auf so eine Aufgabe?). |
Das habe ich doch gemacht oder nicht?
Es sind doch alle Variablen auf einer Seite.
Vielleicht stelle ich mich auch etwas dumm an. Könnte mir das mal jemand vorrechnen mit dem Integral bzw. die Möglichkeit mit dem Energiesatz?
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18078
|
| TomS Verfasst am: 21. Jan 2013 01:11 Titel: |
|
|
Wie gesagt, meine Idee wäre, dies mittels des Energiesatzes zu lösen.
Zu Beginn ist die Gesamtenergie E gleich der potentiellen Energie beim Radius R der Erdbahn (die kinetische Energie ist Null, da die Rotation gestoppt wurde)
 = -GmM/R)
Während des Falls ist die Gesamtenergie E erhalten und ergibt sich als Summe aus kinetischer Energie und potentieller Energie
Daraus ergibt sich ein Zusammenhang zwischen Radius r und Geschwindigkeit v(r) durch Auflösen der Gleichung
nach v(r)
 = \sqrt{2GM\left(\frac{1}{r} - \frac{1}{R}\right)})
Wenn du r(t) als Funktion der Zeit t berechnen möchtest, musst du die DGL lösen. Wenn du jedoch nur an der Falldauer interessiert bist, kannst du die Zeit wie folgt berechnen:
 = \int_0^{T(r)}dt = \int_R^{r(T)}dr\,\frac{dt}{dr} = \int_R^{r}\frac{dr}{v(r)} )
mit der oben bestimmten Funktion v(r).
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 21. Jan 2013 07:07, insgesamt 4-mal bearbeitet |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 21. Jan 2013 01:59 Titel: |
|
|
Kleine Anmerkung: Wenn v in der Formel groesser als Null ist, muss ein fehlt da ein Minuszeichen nach dem letzten Gleicheitszeichen (dr/dt <0, hab da gerade 10min drueber gegruebelt  ).
Und diese Aufgabe ist auch wieder ein schoenes Beispiel dass Dimensionsanalyse einen sehr weit bringt: Da R >> rmin muss das Ergebnis muss proportional zu }) (~ 58 Tage) sein, was nur wenig vom richtigen Wert ~64 Tage abweicht.
|
|
|
buell23
Anmeldungsdatum: 13.11.2006
Beiträge: 238
|
| buell23 Verfasst am: 21. Jan 2013 08:12 Titel: |
|
|
@TomS
Danke für deine Hilfe, jetzt wird es ein wenig klarer.
Wieso hast du in deiner Anfangsgleichung für die potentielle Energie ein Minus bzw. bei der Gesamtenergie?
So komme ich auf -64Tage, was es ja eigentlich nicht gibt?
| jh8979 hat Folgendes geschrieben: | Kleine Anmerkung: Wenn v in der Formel groesser als Null ist, muss ein fehlt da ein Minuszeichen nach dem letzten Gleicheitszeichen (dr/dt <0, hab da gerade 10min drueber gegruebelt ).
Und diese Aufgabe ist auch wieder ein schoenes Beispiel dass Dimensionsanalyse einen sehr weit bringt: Da R >> rmin muss das Ergebnis muss proportional zu (~ 58 Tage) sein, was nur wenig vom richtigen Wert ~64 Tage abweicht. |
Warum sollte da ein Minus kommen, wenn v positiv ist?
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18078
|
| TomS Verfasst am: 21. Jan 2013 08:17 Titel: |
|
|
| buell23 hat Folgendes geschrieben: | | Wieso hast du in deiner Anfangsgleichung für die potentielle Energie ein Minus bzw. bei der Gesamtenergie? |
Weil ein anziehendes 1/r Potential ein Minuszeichen haben muss, sonst läge ein abstoßendes Potential vor.
| buell23 hat Folgendes geschrieben: | | Warum sollte da ein Minus kommen, wenn v positiv ist? |
Weil das Integral von einem größeren R zu kleinerem r läuft. Ein Integral über eine positive Funktion ist größer Null, wenn die untere Integrationsgrenze kleiner ist als die obere. Hier ist das umgekehrt, und deswegen muss die Geschwindigkeit kleiner Null sein.
Anders formuliert ist v = dr/dt, und dr ist kleiner Null, da r(t) mit zunehmender Zeit t abnimmt. Deswegen sollte in meiner Gleichung für die Geschwindigkeit v (r) ein Minus stehen
der Rest passt dann wieder
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 21. Jan 2013 08:25, insgesamt einmal bearbeitet |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 21. Jan 2013 08:23 Titel: |
|
|
| buell23 hat Folgendes geschrieben: |
Warum sollte da ein Minus kommen, wenn v positiv ist? |
Genau deswegen: dr/dt ist negativ, r wird kleiner...
Ansonsten: Einfach das Integral loesen, es ist negativ so wie es dasteht.
|
|
|
buell23
Anmeldungsdatum: 13.11.2006
Beiträge: 238
|
| buell23 Verfasst am: 21. Jan 2013 08:37 Titel: |
|
|
| jh8979 hat Folgendes geschrieben: | | buell23 hat Folgendes geschrieben: |
Warum sollte da ein Minus kommen, wenn v positiv ist? |
Genau deswegen: dr/dt ist negativ, r wird kleiner...
Ansonsten: Einfach das Integral loesen, es ist negativ so wie es dasteht. |
Nun ist alles klar.
| TomS hat Folgendes geschrieben: | | buell23 hat Folgendes geschrieben: | | Wieso hast du in deiner Anfangsgleichung für die potentielle Energie ein Minus bzw. bei der Gesamtenergie? |
Weil ein anziehendes 1/r Potential ein Minuszeichen haben muss, sonst läge ein abstoßendes Potential vor.
| buell23 hat Folgendes geschrieben: | | Warum sollte da ein Minus kommen, wenn v positiv ist? |
Weil das Integral von einem größeren R zu kleinerem r läuft. Ein Integral über eine positive Funktion ist größer Null, wenn die untere Integrationsgrenze kleiner ist als die obere. Hier ist das umgekehrt, und deswegen muss die Geschwindigkeit kleiner Null sein.
Anders formuliert ist v = dr/dt, und dr ist kleiner Null, da r(t) mit zunehmender Zeit t abnimmt. Deswegen sollte in meiner Gleichung für die Geschwindigkeit v (r) ein Minus stehen
der Rest passt dann wieder |
1A erklärt!
Nun wie bringe ich es ohne des Integrals zu einer Lösung mit dem Keppler?
Das hat ja irgendwie nur mit den Umlaufzeiten zu tun.
Ich kenne aber weder die Umlaufzeit noch brauche ich sie für diese Berechnung.
Mir ist nur nicht klar wie ich die Formel des 3. Kepplerschen Gesetzes anwenden soll. (T1/T2)² = (a1/a2)^3
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18078
|
| TomS Verfasst am: 21. Jan 2013 08:55 Titel: |
|
|
Beim Ansatz mittels Kepler betrachtet man den radialen Sturz in die Sonne als entartete Ellipse mit kleiner Halbachse gleich Null. Der Sturz ins Zentrum entspricht dann einem Viertel eines vollen Umlaufs, d.h. T/4. Das Problem ist, wie man die Halbachsen festlegt. Man geht aus von einem Vergleich der Erdbahn mit ihrer bekannten Halbachse und Umaufdauer 365 Tage. Die deformierte Bahn hat jedoch eine andere Halbachse und damit eine andere Umlaufdauer. Die Problematik ist also die physikalische Überlegung, die auf die entartete Ellipse und ihre Halbachse führt. Dazu benötigt man die Darstellung der Geometrie der Ellipse mittels Halbachsen, Brennpunkten sowie der Exzentrizität.
Insgs. finde ich die Herleitung künstlich und bevorzuge die von mir angegebene Lösung, die ohne Kepler auskommt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 21. Jan 2013 10:14, insgesamt 2-mal bearbeitet |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18078
|
|
|
buell23
Anmeldungsdatum: 13.11.2006
Beiträge: 238
|
| buell23 Verfasst am: 21. Jan 2013 11:10 Titel: |
|
|
Hallo Tom
Ich muss noch kurz etwas anderes vorbereiten, ich hätte aber doch noch eine Frage zu deiner Berechnung, dazu muss ich aber selbst noch etwas durchrechnen.
Ich melde mich dann wieder, wenn ich deinen geposteten Link verfolgt und verstanden habe.
Danke für deine bisherige Mühe
|
|
|
D2
Anmeldungsdatum: 10.01.2012
Beiträge: 1723
|
|
|
Systemdynamiker
Anmeldungsdatum: 22.10.2008
Beiträge: 594
Wohnort: Flurlingen
|
| Systemdynamiker Verfasst am: 21. Jan 2013 16:39 Titel: Kepler |
|
|
Kepler ist sicher der einfachste Weg, um zu einer Lösung zu kommen. Genauso einfach ist die numerische Integration. Ein entsprechendes Modell habe ich vor kurzem erstellt. Das dauert nicht mal eine Stunde: http://www.youtube.com/watch?v=rhD110v5nyY
_________________
Herzliche Grüsse Werner Maurer |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18078
|
| TomS Verfasst am: 23. Jan 2013 19:01 Titel: |
|
|
Ich bezweifle dass Kepler der einfachste Weg ist.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
buell23
Anmeldungsdatum: 13.11.2006
Beiträge: 238
|
| buell23 Verfasst am: 23. Jan 2013 20:43 Titel: |
|
|
Mich interessiert das Thema immer noch, komme aber leider nicht dazu mir das Rechenverfahren nochmals genauer anzusehen. Ich denke aber, dass ich mich damit Anfang nächster Woche näher beschäftigen kann.
Also sollte das Thema nicht Vergessenheit geraten von den Leuten, die bereits hilfreiche Inputs gegeben haben.
Was mir aber jetzt schon ein wenig helfen würde ist, wo ich geeignete Aufgaben finde, bei denen ich das Aufstellen eines Integrals zur Lösung der Aufgaben üben kann, da ich in den meisten Fällen Schwierigkeiten damit habe, die Integrale entsprechend aufzustellen, wie es bereits Tom so schön vorgemacht hat.
Einige Tipps wären auch von Nutzen. Verratet mir doch bitte wie ihr bei solchen Themen vorgeht!
Ich bedanke mich bei euch jetzt schon für eure Mühe
|
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5044
|
| DrStupid Verfasst am: 24. Jan 2013 17:47 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | Ich bezweifle dass Kepler der einfachste Weg ist. |
Ich habe da keine Zweifel. Nach Kepler 3 gilt
Die große Halbachse der entarteten Ellipse ist halb so groß wie der Radius der Erdbahn:
und weil die Erde es nur zur Sonne, aber nicht mehr zurück schafft, ist die Flugzeit halb so groß, wie die komplette Umlaufzeit:
Das muss man oben nur noch einsetzen und nach t umstellen:
Natürlich kommt man so nicht zum exakten Wert, weil Erde und Sonne keine Punktmassen sind, aber der Fehler hält sich in Grenzen.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18078
|
| TomS Verfasst am: 24. Jan 2013 19:50 Titel: |
|
|
| DrStupid hat Folgendes geschrieben: | | Die große Halbachse der entarteten Ellipse ist halb so groß wie der Radius der Erdbahn .... |
Das ist richtig, aber nicht unmittelbar einsichtig, oder?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5044
|
| DrStupid Verfasst am: 24. Jan 2013 22:30 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | DrStupid hat Folgendes geschrieben: | | Die große Halbachse der entarteten Ellipse ist halb so groß wie der Radius der Erdbahn .... |
Das ist richtig, aber nicht unmittelbar einsichtig, oder? |
Mir erscheint das selbstverständlich.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18078
|
| TomS Verfasst am: 24. Jan 2013 22:53 Titel: |
|
|
Du musst dir zumindest überlegen, was das bzgl. Radius und Brennpunkt bedeutet. Aber wie gesagt, du hast recht, sobald du diese Festlegung triffst, kommst du auf den korrekten Wert.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Systemdynamiker
Anmeldungsdatum: 22.10.2008
Beiträge: 594
Wohnort: Flurlingen
|
| Systemdynamiker Verfasst am: 25. Jan 2013 06:08 Titel: Einsicht |
|
|
Die Lösung über Kepler ist einfach, sobald man die Idee mit der völlig überdehnten Ellipse (die Brennpunkte fallen mit Aphel und Perihel zusammen) verstanden hat. Vielleicht fühlt man sich auch ein wenig durch den Umstand veräppelt (schweizerisch verarscht), dass man eine komplexe Frage so einfach beantworten kann.
_________________
Herzliche Grüsse Werner Maurer |
|
|
eduard123
Gast
|
| eduard123 Verfasst am: 25. Jan 2013 07:14 Titel: |
|
|
[quote="DrStupid"][quote="TomS"]latex]
Die große Halbachse der entarteten Ellipse ist halb so groß wie der Radius der Erdbahn:
quote]
Irgendwie kann ich mir das nicht vorstellen.
warum R/2?
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18078
|
| TomS Verfasst am: 25. Jan 2013 08:54 Titel: |
|
|
| DrStupid hat Folgendes geschrieben: | | Die große Halbachse der entarteten Ellipse ist halb so groß wie der Radius der Erdbahn .... |
Das ist offensichtlich die Kernaussage, und sowohl hier als auch in anderen Diskussionen stellt sich heraus, dass sie nicht 'offensichtlich klar' oder 'selbstverständlich' ist.
Wir starten mit
wobei T die Umlaufzeiten und a die großen Halbachsen bezeichnet. Der Index 1 bezeichne die tatsächliche Erdbahn, d.h. die Umlaufzeit von einem Jahr sowie (näherungsweise) Erdbahnradius gleich große Halbachse (da fast kreisförmig).
Dann gilt
^{3/2})
Außerdem liegt nun eine zu einem Strich entartete Ellipse vor. Die Fragestellung ist nun, wie die Halbachse dieser entarteten Ellipse festzulegen ist und welchen Teil der Bahn dem Fall der Erde entspricht.
Man könnte meinen, dass man den gegebenen Kreis der Erdbahn mit Radius R einfach zu einer Ellipse platt drückt. Dabei würde die kleine Halbachse Null werden, die große wäre weiterhin gleich dem Radius (= dem aktuellen Abstand). Dieser Ansatz ist falsch, weil für eine entartete Ellipse der Brennpunkt auf der Ellipse selbst liegt, d.h. am Ende des Strichs. Der Brennpunkt ist jedoch der Ort der Sonnen - und man muss natürlich weiterhin annehmen, dass die Erde auf einer plattgedrückten Ellipse mit Sonne im Brennpunkt umläuft.
Das Plattdrücken der Ellipse muss also so erfolgen, dass sich dabei der Ort des einen Brennpunktes = der Sonne nicht ändert. Die Ellipse wird also verkürzt, so dass sie, wenn sie ganz plattgedrückt ist, einem Strich entspricht, an dessen einem Ende = in einem Brennpunkt die Sonne steht, und an dessen anderem Ende die Erde steht (die Position der beiden Himmelskörper hat sich während der Deformation nicht geändert).
Damit ist aber der ursprüngliche Radius der Erdbahn um den Brennpunkt = Mittelpunkt zur gesamten Ellipse entartet, d.h. die neue Ellipse = der Strich entspricht der ursprünglichen Verbindungslinie Erde - Sonne. Damit entspricht der alte Radius dem Doppelten der neuen großen Halbachse, d.h. die neue Halbachse gleich der Hälfte des alten Radius.
Dazu eine Zeichnung auf Seite 25 in
http://sternwarte-recklinghausen.de/data/uploads/dateien/pdf/keplerellipsen.pdf
Damit wird aus der o.g. Gleichung
Nun entspricht aber die Falldauer gleich der Hälfte der gesamten Umlaufdauer auf der neuen Ellipse, und damit folgt
Es ist natürlich genau diese physikalische Überlegung, die die Argumentation so interessant macht. Aber die Aussage, dass die Herleitung mit Kepler-3 die einfachste wäre und dass die o.g. Beziehungen 'selbstverständlich' sind, verschweigt zunächst genau diese Überlegung.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5044
|
| DrStupid Verfasst am: 25. Jan 2013 18:57 Titel: |
|
|
| eduard123 hat Folgendes geschrieben: | | DrStupid hat Folgendes geschrieben: |
Die große Halbachse der entarteten Ellipse ist halb so groß wie der Radius der Erdbahn:
|
Irgendwie kann ich mir das nicht vorstellen.
warum R/2? |
Wenn Du das Aphel auf der Erdbahn lässt und die Geschwindigkeit in diesem Punkt verringerst, dann wandert das Perihel näher an die Sonne. Bremst man den Körper im Aphel komplett ab, dann geht auch der Perihelabstand gegen Null. Das Ergebnis ist eine "Ellipse" deren eines Ende in der Sonne und das andere auf der Erdbahn sitzt. Die Länge dieser Ellipse enspricht also dem Erdbahnradius und ihre große Halbachse ist (wie der Name schon vermuten läst) halb so groß.
|
|
|
|
Registrieren
Login
FAQ
Suchen
