| Autor |
Nachricht |
Külle007
Gast
|
 Külle007 Verfasst am: 17. Aug 2004 20:41 Titel: Hammerwerfen (Kreisbewegung, Wurfbewegung) Külle007 Verfasst am: 17. Aug 2004 20:41 Titel: Hammerwerfen (Kreisbewegung, Wurfbewegung) |
 |
|
Habe folgende Aufgabe und komm einfach nicht an einen Ansatz:
| Zitat: | Informationen:
- Hammerwerfer beschleunigt Wurfgerät so,dass es in der letzten Bewegungsphase einer gleichförmige Kreisbewegung mit einem Durchmesser der geneigten Kreisbahn von 5m mit dem Kreismittelpunkt P0 entspricht
- P0 sowie 2 weitere Positionen P1 und P2 kart. bekannt
| Code: | Position x[m] y[m] z=h[m] Zeitpunkt [s]
P0 0,000 0,000 1,700 ------
P1 2,034 -0,740 0,450 0,000
P2 1,083 1,875 2,950 0,150 |
- Der Hammer wird an dem Punkt der geneigten Ebene losgelassen, wenn Seil des Hammers horizontal verläuft und der Hammer sich in der Aufwärtsbewegung befindet
Aufgaben:
1. Drehgeschwindigkeit der Kreisbewegung bestimmen
2. Umlaufzeit+Anzahl der Bewegungen in der Minute
3. Bestimmung der Geschwindigkeitsvektoren zu den Zeitpunkten t1, t2 und des Loslassens
4. Beschleunigungsvektor zum Zeitpunkt t1
5. Wurfweitedes Hammers und Dauer der Flugphase
6. Maximale Höhe
7. Geschwindigkeit und Aufschlagwinkel des Hammers auf dem Boden
8. Wenn losgelassen am höchsten Punkt: Wurfweite+max. Höhe? |
Bei den einzelnen Teilen der Aufgabe tue ich mich sehr schwer und komme teilweise auf gar keine Lösung. Hätte sehr gerne Hilfe oder lieber noch eine nachvollziehbare Musterlösung.
Danke im Voraus,
Gruß Külle  |
|
 |
Nikolas
Ehrenmitglied

Anmeldungsdatum: 14.03.2004
Beiträge: 1873
Wohnort: Freiburg im Brsg.
|
 Nikolas Verfasst am: 17. Aug 2004 23:53 Titel: Nikolas Verfasst am: 17. Aug 2004 23:53 Titel: |
 |
|
Ich fang mal mit 5 an:
5) Wurfweite/Flugdauer: Aus den Bahnkoordinaten kannst du dir den Abflugwinkel und Geschwindigkeit errechnen. (frag nochmal, wenn's hier Probleme gibt.) Dann zerlegst du diesen Vektor in senkrecht und waagrecht Anteil. Mit dem waagrecht Anteil kannst per
x=g/2*t²+v(Senkrecht)*t+HöheDesHammersBeimStart die Flugdauer berechnen. Jetzt nimmst du diese Zeit und setzt sie in eine Gleichung mit der waagrechten Geschwindigkeit ein: x'=v(waagrecht)*t(grad ausgerechnet). Dieses x' ist die Wurfweite.
6) max Flughöhe: Energieerhaltungssatz: Die Energie in der Senkrecht Bewegung ist gleich der Lageenergie im höchsten Punkt, Also
m/2*v(senkrecht)²=m*g*MaxHöhe;
7) Der Winkel zwischen der v(ges) und der Senkrechten entspricht dem Anflugwinkel. V(waagrecht) und v(senkrecht) bekommst du über die Flugzeit. Die Aufschlaggeschwindigkeit bekommst du über einen Phytagoras
8 ) Max: Flughöhe: Höhe beim Loslassen, da der Hammer dann senkrecht zum Boden abhaut un nurnoch an Höhe verliert. Weite: Wie oben über die Formeln errechnen.
Schreib doch mal wie weit du schon gekommen bist. Eine Musterlösung gibt's erstmal nicht. 
Tox
_________________
Nikolas, the mod formerly known as Toxman.
Erwarte das Beste und sei auf das Schlimmste vorbereitet. |
|
 |
Külle007
Gast
|
 Külle007 Verfasst am: 18. Aug 2004 07:19 Titel: Re: Külle007 Verfasst am: 18. Aug 2004 07:19 Titel: Re: |
 |
|
Genau über diese Aufgabenteile habe ich mir auch Gedanken gemacht, bin auch zu ähnlichen Lösungsansätzen gekommen. Gerechnet wird noch selber!;-)
Was mir aber noch Kopfzerbrechen bereitet, ist in erstet Linie der Aufgabenteil 1.1. Hier seh ich den entsprechenden Zusammenhang zwischen den vorgegebenen Werten und den weiterhin bekannten Informationen noch nicht, um auf die Lösung zu kommen.
Hst du eine Idee?
Gruß Külle |
|
 |
devzero
Anmeldungsdatum: 04.08.2004
Beiträge: 68
|
 devzero Verfasst am: 18. Aug 2004 08:13 Titel: devzero Verfasst am: 18. Aug 2004 08:13 Titel: |
 |
|
Nette Frage, Külle007! Starte doch so:
Die Vektoren v1=P1-P0 und v2=P2-P0 sind beides "Radiusvektoren", d.h. sie liegen in der Ebene der Kreisbewegnung. Den Zwischenwinkel kann man dann per =\frac {\vec v_1 \cdot \vec v_2} {|\vec v_1| \, |\vec v_2|}) berechnen. Zu beachten ist, dass der cos < 0 ist, d.h. der Winkel alpha ist stumpf (1.69 rad). Die Winkelgeschwindigkeit ist dann berechnen. Zu beachten ist, dass der cos < 0 ist, d.h. der Winkel alpha ist stumpf (1.69 rad). Die Winkelgeschwindigkeit ist dann  = 11.2 rad/s) . Das sollte fuer Teil 1+2 reichen. . Das sollte fuer Teil 1+2 reichen.
3. Da wuerde ich den Normalenvektor auf die Kreisebene ausrechnen: 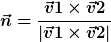 . Geschwindikeitsvektoren sind immer sowohl senkrecht zu v1 bzw. v2 und auch n, also wieder Kreuzprodukt zwischen n und v1 bzw. v2 bilden. Den Betrag der Geschwindigkeit musst du nachtraeglich noch anpassen, aber du weisst wohl, wie das geht. . Geschwindikeitsvektoren sind immer sowohl senkrecht zu v1 bzw. v2 und auch n, also wieder Kreuzprodukt zwischen n und v1 bzw. v2 bilden. Den Betrag der Geschwindigkeit musst du nachtraeglich noch anpassen, aber du weisst wohl, wie das geht.
4. Beschleunigung ist in (umgekehrter) v1-Richtung. Betrag wieder anpassen.
5. Abschlusswinkel ist Neigung der Rotationsebene/Normalenvektors gegen den Einheitsvektor in z-Richtung. Winkel wieder mit cos - wie bei Teil 1
Reicht dir das als "Starthilfe"? Melde dich sonst nochmal.
Zuletzt bearbeitet von devzero am 18. Aug 2004 18:59, insgesamt einmal bearbeitet |
|
 |
Külle007
Gast
|
 Külle007 Verfasst am: 18. Aug 2004 10:15 Titel: Re: Külle007 Verfasst am: 18. Aug 2004 10:15 Titel: Re: |
 |
|
Danke für die Ansätze!
Hab bisher noch nie viel Zeit für Physik verwenden können und bin jetzt erstaunt,dass man viele Dinge wohl doch -i.d.F zumindestens- mit Grundlagen der Vektoralgebra lösen kann.
Gruß, Külle |
|
 |
Külle007
Gast
|
 Külle007 Verfasst am: 21. Aug 2004 16:37 Titel: Bestimmung der Koordinate des Abwurfpunktes Külle007 Verfasst am: 21. Aug 2004 16:37 Titel: Bestimmung der Koordinate des Abwurfpunktes |
 |
|
|
Habe desweiteren das Problem, die Koordinate des Abwurfpunktes zu bestimmen.Für den Betrag der beiden Geschwindigkeitsvektoren zu den Zeitpunkten P0 und P1 habe ich 1 herausbekommen, sodass ich davon ausgehe, dass dies auch der Betrag für den Abwurfpunkt P3 gilt. Für den Vektor von P3 fehlen die x und y-Koordinate. Wie kann ich die berechnen? |
|
 |
devzero
Anmeldungsdatum: 04.08.2004
Beiträge: 68
|
 devzero Verfasst am: 22. Aug 2004 12:26 Titel: devzero Verfasst am: 22. Aug 2004 12:26 Titel: |
 |
|
Der Radiusvektor zum Loslass-Zeitpunkt t3 ist senkrecht zum Ebenenvektor des Kreises und dem Einheitszektor in z-Richtung (da horizontal). Wenn du das Kreuzprodukt bildest hast du die Richtung. Laenge noch anpassen und P0 dazuaddieren nivht vergessen.
Was ist das eigentlich fuer 'ne Aufgabe? |
|
 |
Külle007
Gast
|
 Külle007 Verfasst am: 22. Aug 2004 14:57 Titel: Re: Külle007 Verfasst am: 22. Aug 2004 14:57 Titel: Re: |
 |
|
|
Stammt aus nem Leistungsnachweis für Technik-Studium von ner FH. |
|
 |
Külle
Anmeldungsdatum: 17.08.2004
Beiträge: 4
|
 Külle Verfasst am: 22. Aug 2004 17:36 Titel: weiteres Problem Külle Verfasst am: 22. Aug 2004 17:36 Titel: weiteres Problem |
 |
|
ich beiß mich an dieser Aufgabe fest& komm nicht so wirklich zu einem zufriedenstellenden Ergebnis.
Die Tipps sind logisch,nur mit meinen Werten komm ich im Endeffekt, nachdem ich P3 berechnet habe, nicht mehr auf den Radius 2,5 m.
Der Normalenvektor lautet bei mir:
n=(0,2287;-0,628;07439),
der Einheitsvekor entsprechend e=(0,0,1).
Mit dem Kreuzprodukt erhalte ich r(t3)=(0,628;0,2287;0).
P3 dann über
P3=P0+2,5*(0,628;0,2287;0) <=> P3=(1,57;0,57175;1,7).
Kontrolle für den Radius von 2,5 m wäre trig. Pyth. über P0 und P3.
Das passt so nicht. Wo liegt mein Fehler....?![/i][/code][/list] |
|
 |
devzero
Anmeldungsdatum: 04.08.2004
Beiträge: 68
|
 devzero Verfasst am: 23. Aug 2004 17:33 Titel: devzero Verfasst am: 23. Aug 2004 17:33 Titel: |
 |
|
|
Achtung: Das Kreuzprodukt von zwei Einheitsvektoren ist selber i.A. kein Einheitsvektor (Sinus vom Zwischenwinkel). Dein r(t3) ist zu kurz, normiert ist er {0.94, 0.34, 0.}. Dann folgt fuer P3={2.35, 0.86, 1.7} und auch mit dem Radius stimmt wieder alles. |
|
 |
Külle007
Gast
|
 Külle007 Verfasst am: 25. Aug 2004 09:09 Titel: Re: Külle007 Verfasst am: 25. Aug 2004 09:09 Titel: Re: |
 |
|
Habe die Aufgabe bis auf den letzten Punkt gelöst. Welche Annahmen kann ich stellen, dass ich den höchsten Punkt berechnen kann?
Desweiteren habe ich für die Aufschlaggeschw. einen Wert von 27,624m/s, für den Aufschlagwinkel einen Wert von a=31,9733gon. Könnte mir bitte jmd die Werte bestätigen? Bei anderen Werten hätte ich gerne einen Lösungsweg.
Danke für die bisherigen Hilfen & Beiträge,
Gruß Külle |
|
 |
Teufelus
Anmeldungsdatum: 11.04.2004
Beiträge: 62
Wohnort: Hannover
|
 Teufelus Verfasst am: 25. Aug 2004 21:32 Titel: Teufelus Verfasst am: 25. Aug 2004 21:32 Titel: |
 |
|
Für die Wurfhöhe gilt:  |
|
 |
|

















