| Autor |
Nachricht |
doublesobig
Anmeldungsdatum: 20.12.2021
Beiträge: 5
|
 doublesobig Verfasst am: 20. März 2022 20:51 Titel: Kreisbewegung durch unelastischen Stoß doublesobig Verfasst am: 20. März 2022 20:51 Titel: Kreisbewegung durch unelastischen Stoß |
 |
|
Meine Frage:
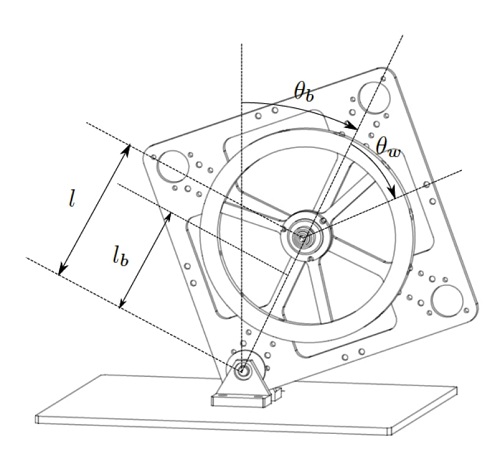
Wir erarbeiten von der Uni aus in einem Projekt einen Würfel, der auf Kanten oder Ecken balancieren kann. Aktuell erarbeiten wir uns grundlegende Erkenntnisse mit Hilfe eines Prototypen, der nur aus einer Würfelwand und einem, an einem Motor befestigten, Schwungrad besteht.
(Hier ein Link zu einer Skizze unseres Protoypen: )
Bild aus externem Link als Anhang eingefügt. Bitte keine solche Links verwenden. Steffen
Wir haben für die Physik hinter dem Projekt leider keinen genauen Arbeitsauftrag bekommen. (Physik spielt in unserem Lehrplan leider auch keine Rolle)
Weiterhin ist am dem Prototyp eine IMU befestigt, mit der wir die Winkelgeschwindigkeit und die Auslenkung des Prototyps zu jedem Zeitpunkt feststellen können.
Mit Hilfe des Gyroskops erhalten wir die Winkelgeschwindigkeit des Prototypen beim Umkippen. Dadurch lässt sich sehr einfach die Rotationsenergie bestimmen.
Mit diesem Wissen können wir eine theoretische Drehzahl des Schwungrades berechnen, die die gleiche Rotationsenergie des kippenden Prototypen erzeugt.
Jetzt wäre es noch interessant, welche Energie mit dem Schwungrad erzeugt werden muss, um den Prototypen wieder in eine aufrechte "Balance"-Position zu bringen.
Hier wäre mein Ansatz, eine Kraft durch einen unelastischen Stoß (durch Beschleunigen/Abbremsen des Schwungrades) zu berechnen, welche den Körper auf der Kreisbahn beschleunigt.
An dieser Stelle weiß ich jedoch leider nicht mehr, wie ich weiter vorgehen kann.
Meine Ideen:
Aufgrund der Auslenkungsberechnung würde sich eine zu bewältigende Strecke berechnen lassen.
Der Radius ist bekannt (ich nehme hier den Abstand des Massenschwerpunkts zum Rotationsmittelpunkt an).
Trägheitsmomente sind für Schwungrad und Prototyp bekannt.
| Beschreibung: |
|
| Dateigröße: |
47.08 KB |
| Angeschaut: |
1325 mal |
|
|
|
 |
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3398
|
 ML Verfasst am: 21. März 2022 07:53 Titel: Re: Kreisbewegung durch einen unelastischer Stoß ML Verfasst am: 21. März 2022 07:53 Titel: Re: Kreisbewegung durch einen unelastischer Stoß |
 |
|
Hallo,
| doublesobig hat Folgendes geschrieben: |
An dieser Stelle weiß ich jedoch leider nicht mehr, wie ich weiter vorgehen kann.
|
Meines Erachtens solltest Du Dich zunächst mit dem Begriff des Drehimpulses (und seiner Erhaltung) sowie mit Regelungstechnik auseinandersetzen und mit einer Person, die sich auskennt, klären, ob für eine solche Anordnung ein normaler PID-Regler ausreicht. (An sich ist das ja ein inverses Pendel, es sollte m. E. ausreichen).
Ein Drehratensensor hat eine Drift. Du wirst auf Dauer mit ihm nicht herausfinden können, in welchem Winkel sich die Anordnung befindet. Zusätzlich brauchst Du m. E. einen Beschleunigungssensor.
Viele Grüße
Michael
|
|
 |
doublesobig
Anmeldungsdatum: 20.12.2021
Beiträge: 5
|
 doublesobig Verfasst am: 21. März 2022 14:39 Titel: doublesobig Verfasst am: 21. März 2022 14:39 Titel: |
 |
|
Die Regelungstechnik erarbeiten wir bereits.
Es geht hier nur um einen groben Blick auf den physikalischen Hintergrund.
Ich wollte über die Messung der Auslenkung nicht zu viele Worte verlieren, da es in diesem Kontext nicht hilfreich ist. Der Drift ist uns bekannt und wird durch einen Komplementärfilter mit einer Kombination aus Gyro und Accelerometer korrigiert.
Vielen Dank für den Tipp mit dem Drehimpuls. Ich werde mal etwas suchen, jedoch weiß ich nicht wie sehr mir der Drehimpuls helfen kann.
|
|
 |
gast_free
Anmeldungsdatum: 15.07.2021
Beiträge: 195
|
 gast_free Verfasst am: 22. März 2022 14:53 Titel: gast_free Verfasst am: 22. März 2022 14:53 Titel: |
 |
|
Relevant ist wohl die Theorie vom schnellen Kreisel (Gyroskope).
Dreht sich ein schneller Kreisel mit der Winkelgeschwindigkeit omega um seine eigene Achse, lässt sich ein Drehmoment M erzeugen, wenn man diesen schnell rotierenden Kreisel mit der Winkelgeschwindigkeit Omega aus seiner Rotationsrichtung dreht.

JF ist das Massenträgheitsmoment um die Rotationsachse des Kreisel selbst. Wie aus dem Vektorprodukt ersichtlich, steht das Drehmoment senkrecht auf den beiden Hauptrotationsvektoren. Man kann nun rechnerisch Momentengleichungen aufstellen und die Winkelgeschwindigkeit Omega berechnen die nötig ist, damit sich der Kreisel um seine Befestigung auf der Platte gegen die Schwerkraft bewegt.
|
|
 |
|
|
















