| Autor |
Nachricht |
Hix
Anmeldungsdatum: 17.05.2005
Beiträge: 2
Wohnort: Linz
|
 Hix Verfasst am: 27. Mai 2005 14:35 Titel: Massen auf Kreisfedern Hix Verfasst am: 27. Mai 2005 14:35 Titel: Massen auf Kreisfedern |
 |
|
Hi!
Also ich hab da folgendes Problem, dass ich lösen soll, aber irgendwie funzts nicht so richtig:
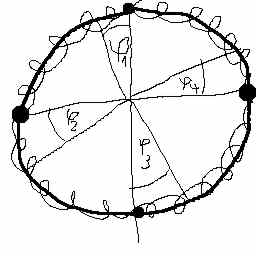
Auf einem kreisrunden Draht sind 4 Massen angebracht (m1=m3,m2=m4), sodass sie sich entlang des Umfangs bewegen können und die winkel zwischen den Massen sind jeweils 90°.
Die Massen sind jetzt durch Federn mit Federkonstante k miteinander verbunden, wobei die Federn rund um den Drahtkreis gelegt sind.
Ich soll jetzt die Normalschwingungen und die Eigenfrequenzen bestimmen, wobei man 2 Normalschwingungen dadurch bestimmen soll, dass man die Symmetrie des Systems ausnutzt und die anderen zwei dadurch, dass man die Beziehungen zwischen den Auslenkungen der massen ausnützt und somit das 4x4 Gleichungsystem auf 2x2 herunterbekommt.
Das ist die Angabe, so wie ich sie bekommen habe.
| Beschreibung: |
|
| Dateigröße: |
8.96 KB |
| Angeschaut: |
1367 mal |
|
_________________
Be careful what you wish you just may get it
Be careful what you wish you might regret it
Zuletzt bearbeitet von Hix am 27. Mai 2005 15:33, insgesamt einmal bearbeitet |
|
 |
Hix
Anmeldungsdatum: 17.05.2005
Beiträge: 2
Wohnort: Linz
|
 Hix Verfasst am: 27. Mai 2005 15:28 Titel: Die Rechnung Hix Verfasst am: 27. Mai 2005 15:28 Titel: Die Rechnung |
 |
|
Also erstmal die Ausdrücke für Energie:
T...kinetische Energie
V...Potentielle Energie
p1,p2,p3,p4...Phi1,Phi2,Phi3,Phi4
pp1,pp2,pp3,pp4...d(Phi1)/dt,d(Phi2)/dt,....
p...Vector(p1,p2,p3,p4)
c1,c2,c3,c4....Auslenkungen der einzelnen Massen
c...Vector(c1,c2,c3,c4)
pp...Vector... (pp1,pp2,pp3,pp4)
ppp... Vector (d/dt)pp
r...Radius
k...Federkonstante
T=(r^2)/2*m1*(pp1^2+pp3^2)+(r^2)/2*m2*(pp2^2+pp4^2)
und
V=k*r^2/2((p1-p2)^2+(p2-p3)^2+(p3-p4)^2+(p4-p1)^2)
das ganze jetz in Matrixschreibweise ist
T=(r^2)/2*pp*A*pp+(k*r^2)/2*p*K*p
mit A=((m1,0,0,0),(0,m2,0,0),(0,0,m1,0),(0,0,0,m2))
und K=((2,-1,0,-1),(-1,2,-1,0),(0,-1,2,-1),(-1,0,-1,2))
Lagrange-Gleichungen aufstellen:
L=T-V
(d/dt)(d/dpp)L-(d/dp)L=0
daraus folgt:
(r^2)/2*A*ppp+k*(r^2)*K*p=0
weiters mit Ansatz p=c*e^(iwt)
k*K*p-A*(w^2)/2*p=0
nun p herausheben und dann e^(iwt) rauskürzen (ist eh immer ungl. 0)
[kK-A(w^2)/2]c=0
wenn c=(0,0,0,0) hab ich die triviale Lösung (es schwingt eigentlich nix)
wenn c ungl. 0 dann muss die Matrix in der Klammer linear abhängig sein, und daduch auch die Determinante verschwinden.
also det[kK-A(w^2)/2]=0 daraus krieg ich dann eine gleichung 4.Ordnung, welche ich nicht wirklich lösen kann (Computer kanns)
wenn ich jetzt auf die Symmetrie zurückkomme, kann ich sagen:
wenn c=(c1,c2,c3,c4) eine Lösung dieser gleichung ist, dann muss auch c=(c3,c4,c1,c2) eine Lösung sein, weil ich die massen m1 und m3 austauschen kann, und sich nichts am system ändert, genauso mit m2 und m4.
Also c1=c3, und c2=c4 (da bin ich mir aber nicht so sicher).
wie könnte man aus dieser Information die Normalschwingungen sehen??
und wie sollte man aus der "Beziehung" der gegenüberliegenden Massen das Gleichungssystem von 4 auf 2 Dimensionen reduzieren??
Naja, vielleicht kennt ja jemand das Problem, oder es sonst wer gerade Muse sich das zu überlegen, wenn ich auf was komm, dann wirds gleich gepostet
_________________
Be careful what you wish you just may get it
Be careful what you wish you might regret it |
|
 |
Henry
Anmeldungsdatum: 16.05.2005
Beiträge: 22
|
 Henry Verfasst am: 28. Mai 2005 23:08 Titel: Henry Verfasst am: 28. Mai 2005 23:08 Titel: |
 |
|
Die 4 von dir angegebenen Bewegungsgleichungen haben folgende Form:
)
)
)
)
Das Problem hat zwei Symmetrieachsen:
1. Die Achse zwischen den Massen m2 und m4.
2. Die Achse zwischen den Massen m1 und m3.
Symmetrie bedeutet aber, dass sich im ersten Fall die Massen m2 und m4 und im zweiten Fall m1 und m3 nicht verschieben dürfen. Daraus folgt aber sofort:


Damit können aus den obigen Gleichungen die ersten beiden EF'en berechnet werden. Das gleiche Ergebnis erhält man ohne große Überlegung, wenn man die 3. von der 1. bzw. die 4. von der 2. Gleichung abzieht:
 + 2 \ k \ (\ddot \phi_1 - \ddot \phi_3) = 0)
 + 2 \ k \ (\ddot \phi_2 - \ddot \phi_4) = 0)
Daraus lassen sich folgende zwei Eigenfrequenzen ermitteln:

Die anderen beiden Lösungen ergeben sich aus der Addition der genannten Gleichungen:
 + 2 \ k \ (\ddot \phi_1 + \ddot \phi_3) = 2 \ k\ (\phi_2 + \phi_4))
 + 2 \ k \ (\ddot \phi_2 + \ddot \phi_4) = 2 \ k\ (\phi_1 + \phi_3))
Dieses System aus nur zwei DGL'en ist z.B. durch das Überführen in eine DGL 4. Ordnung relativ einfach lösbar. Aus dieser DGL ergeben sich dann die restlichen zwei EF'en.
PS: Eine Reaktion wäre schon nicht schlecht gewesen??? 
|
|
 |
|
|

















