| Autor |
Nachricht |
Cypr3s
Gast
|
 Cypr3s Verfasst am: 25. Mai 2011 10:48 Titel: Eigenschwingung einer Gitarrensaite |
 |
|
Meine Frage:
Hallo,
ich stehe vor einem Problem bzw. ich weiß nicht so recht was ich machen soll.
Meine Aufgabe lautet: "Untersuchen sie die möglichen Eigenschwingungen der einzelnen Saiten und entwickeln sie eine Formel zur Berechnung dieser.Gehen sie dabei näher auf das Konzept der stehenden Welle ein."
In der Aufgabe steht noch, die Saiten sind 64cm lang.
Da ich meinen Lehrer nicht fragen darf, wollt ich euch zum Verständnis etwas fragen:
Was ist denn genau mit der Eigenschwingung gemeint?
Meine Ideen:
Das Prinzip einer stehenden Welle ist mir einigermaßen klar. Wenn ich eine Saite zupfe dann entsteht ja eine Frequenz, welche in der Gitarre reflektiert wird. Dabei kommt es ja zu eine Überlagerung der erzeugten und der reflektierten Welle, sodass eine stehende Welle erzeugt wird.
Aber ich bin mir, wie gesagt, bei der Berechnung der Eigenschwingung unsicher. |
|
 |
lampe16
Anmeldungsdatum: 21.03.2010
Beiträge: 319
|
| lampe16 Verfasst am: 26. Mai 2011 19:57 Titel: Re: Eigenschwingung einer Gitarrensaite |
|
|
| Cypr3s hat Folgendes geschrieben: | | Was ist denn genau mit der Eigenschwingung gemeint?unsicher. |
Wenn man ein schwingungsfähiges Objekt irgendwie anstößt, dann aber nicht mehr eingreift, d.h. keine äußeren Kräfte mehr aufprägt, dann schwingt es mit seiner (oder seinen) Eigenschwingung(en).
Beispiele: Schaukel, Glocke, Schraubenfeder mit angehängter Masse, angezupfte Saite.
Die Eigenschwingung einer Seite (an den Enden ist der Ausschlag gleich null) schwingt räumlich und zeitlich harmonisch (sin-förmig).
Die Eigenfrequenz  (Frequenz der Eigenschwingung) hängt vom Massebelag 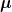 der Saite (kg/m) und der Zugkraft  in der Saite (N) ab.
Es gilt die Formel
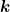 ist die Anzahl der räumlichen Halbwellen der Schwingung. Die Schwingung mit der niedrigsten Eigenfrequenz heißt Grundschwingung (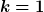 ). Die Eigenschwingungen mit  Halbwellen heißen Oberschwingungen oder höhere Harmonische.
Die Frequenzformel lässt sich aus einer partiellen Differentialgleichung herleiten, was aber sicher nicht mehr Schulstoff ist.
_________________
Herzliche Grüße, Lampe16
_________________________________________
Hard work beats talent if talent doesn't work hard. |
|
|
Cypr3s
Gast
|
| Cypr3s Verfasst am: 27. Mai 2011 11:46 Titel: |
|
|
Vielen Dank für die Antwort! Das hat mir wirklich geholfen.
Eine Sache ist mir aber noch nicht ganz klar:
Die Grundschwingung hat eine Frequenz von 
Die 1. Oberschwingung hat dann ja die Frequenz von 
Nur wo genau tritt diese Oberschwingung jetzt auf?
Also was genau schwingt jetzt in der Oberschwingung? Die Saite? |
|
|
lampe16
Anmeldungsdatum: 21.03.2010
Beiträge: 319
|
| lampe16 Verfasst am: 27. Mai 2011 12:10 Titel: |
|
|
| Cypr3s hat Folgendes geschrieben: | Nur wo genau tritt diese Oberschwingung jetzt auf?
Also was genau schwingt jetzt in der Oberschwingung? Die Saite? |
Sichtbar wird die Oberschwingung in der Auslenkungsform der Saite. Man könnte sie mit einer Hochgeschwindigkeitskamera photographieren. Bei der 2. Harmonischen (1. Oberschwingung) bildet die Saite in jedem Augenblick eine volle Sinusperiode (von 0 bis 360°= 2*180°) aus. Bei der 3. Harmonischen geht der Sinus von 0 bis 3*180° usw..
Eine einzelne Harmonische tritt praktisch nie auf. Um das zu erreichen, müsste man die Saite in der betreffenden Sinusform auslenken und dann loslassen. Wenn man die Saite dreieckförmig auslenkt (Näherung für Zupfen), entstehen alle die Harmonischen einschl. der Grundharmonischen, die zusammen die Dreieckform ergeben.
_________________
Herzliche Grüße, Lampe16
_________________________________________
Hard work beats talent if talent doesn't work hard. |
|
|
Cypr3s
Gast
|
| Cypr3s Verfasst am: 28. Mai 2011 12:04 Titel: |
|
|
ahh ok.
Eine Frage hab ich noch:
Ich versuch die ganze Zeit die Formel irgendwie herzuleiten.
Hat die Formel einen bestimmten Namen? |
|
|
lampe16
Anmeldungsdatum: 21.03.2010
Beiträge: 319
|
| lampe16 Verfasst am: 29. Mai 2011 16:06 Titel: |
|
|
Die Formel entsteht aus der partiellen Differentialgleichung der transversal schwingenden Saite
}{\partial x^2}=\frac{\mu}{S}\frac{\partial^2 w(x,t)}{\partial t^2}.)
Wenn du für die Auslenkung
=\hat W \sin 2\pi f_e t \cdot\sin\frac{k\pi}{L}x)
ansetzt, siehst du, dass der Ansatz die Dgl. erfüllt und kannst daraus die Eigenfrequenzformel herleiten. Einen besonderen Namen hat sie nicht.
_________________
Herzliche Grüße, Lampe16
_________________________________________
Hard work beats talent if talent doesn't work hard. |
|
|
|
|
Registrieren
Login
FAQ
Suchen
